2021北京四中初一（下）期中数学（教师版）

这是一份2021北京四中初一（下）期中数学（教师版），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021北京四中初一（下）期中
数 学
一、选择题
1. 下列各图中，∠1和∠2是对顶角的是（　　）
A. B.
C. D.
2. 的平方根是（　　）
A. 3 B. ±3 C. D. ±
3. 点(﹣4，2)所在的象限是（　　）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 下列长度的三条线段能组成三角形的是（　　）
A. 3，4，8 B. 5，6，11 C. 4，4，8 D. 8，8，8
5. 多边形的边数由3增加到2021时，其外角和的度数（　　）
A. 增加 B. 减少 C. 不变 D. 不能确定
6. 以下命题是真命题的是（　　）
A. 相等的两个角一定是对顶角
B. 过直线外一点有且只有一条直线与已知直线平行
C. 两条平行线被第三条直线所截，内错角互补
D. 在同一平面内，垂直于同一条直线的两条直线互相垂直
7. 如图，下列条件： ①∠DCA=∠CAF，②∠C =∠EDB，③∠BAC+∠C=180°，④∠GDE +∠B=180°．其中能判断AB∥CD的是（ ）

A. ①④ B. ②③④ C. ①③④ D. ①②③
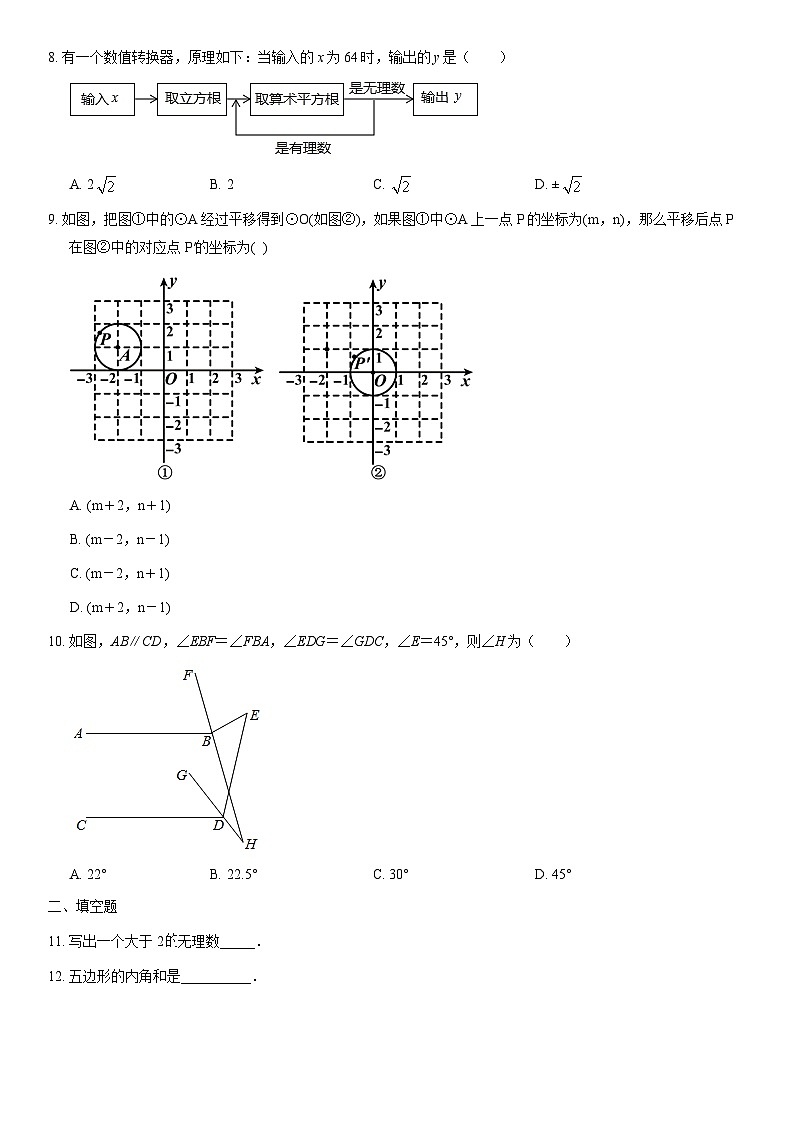
8. 有一个数值转换器，原理如下：当输入的x为64时，输出的y是（　　）

A. 2 B. 2 C. D. ±
9. 如图，把图①中的⊙A经过平移得到⊙O(如图②)，如果图①中⊙A上一点P的坐标为(m，n)，那么平移后点P在图②中的对应点P′的坐标为( )

A. (m＋2，n＋1)
B. (m－2，n－1)
C. (m－2，n＋1)
D. (m＋2，n－1)
10. 如图，AB∥CD，∠EBF＝∠FBA，∠EDG＝∠GDC，∠E＝45°，则∠H为（　　）

A. 22° B. 22.5° C. 30° D. 45°
二、填空题
11. 写出一个大于2无理数_____．
12. 五边形的内角和是__________．
13. 如图是玉渊潭公园部分景点分布示意图，在图中，分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系，当表示西桥的点的坐标为，表示中堤桥的点的坐标为时，表示留春园的点的坐标为___.

14. 如图，将三角板的直角顶点放在直尺的一边上，∠1＝30°，∠2＝50°，则∠3=__________°．

15. 等腰三角形的边长分别为6和8，则周长为___________________．
16. 如图，直线11⊥12，在某平面直角坐标系中，x轴∥l1，y轴∥12，点A的坐标为(﹣2，4)，点B的坐标为(4，﹣2)，那么点C在第___象限．

17. 在1～7月份，某种水果的每斤进价与每斤售价的信息如图所示，则出售该种水果每斤利润最大的月份是_____月份．

18. 小明用计算器求了一些正数的平方，记录如下表．
x
26
26.1
26.2
26.3
26.4
26.5
26.6
26.7
26.8
26.9
27
x2
676
681.21
686.44
691.69
696.96
702.25
707.56
712.89
718.24
723.61
729
下面有四个推断：
①＝262；
②一定有6个整数的算术平方根在26.6～26.7之间；
③对于小于26的两个正数，若它们的差等于0.1，则它们的平方的差小于5.21；
④若一个正方形的边长为26.4，那么这个正方形的面积是696.96．
所有合理推断的序号是___．
三、解答题
19. 计算：．
20. 解下列方程：
（1）2x3＝﹣16；
（2）25（x2﹣1）＝24．
21. 完成下面推理填空：
如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G．
求证：ABCD．
证明：∵AF⊥CE
∴∠CGF＝90° （　 　）
∵∠1＝∠D（已知）
∴　 　　 　（　 　）
∴∠4＝∠CGF＝90°（　 　）
∵∠2+∠3+∠4＝180°（平角的定义）
∴∠2+∠3＝90°．
∵∠2与∠C互余（已知），
∴∠2+∠C＝90°（互余的定义）
∴∠C＝∠3（同角的余角相等）
∴ABCD （　 　）

22. 已知点A(3a﹣6，a+1)，试分别根据下列条件，求出点A的坐标，
（1）点A在x轴上；
（2）点A在过点P(3，﹣2)，且与y轴平行的直线上．
23. 如图，在ABC中，AE平分∠BAC，AD是BC边上的高．
（1）在图中将图形补充完整；
（2）当∠B＝28°，∠C＝72°时，求∠DAE的度数；
（3）∠DAE与∠C﹣∠B有怎样的数量关系？写出结论并加以证明．

24. 如图，在正方形网格中，横、纵坐标均为整数的点叫做格点，点A、B、C、O均在格点上，其中O为坐标原点，A(﹣3，3)．
（1）点C的坐标为　 　；
（2）将ABC向右平移6个单位，向下平移1个单位，对应得到A1B1C1，请在图中画出平移后的A1B1C1，并求A1B1C1的面积；
（3）在x轴上有一点P，使得PA1B1的面积等于A1B1C1的面积，直接写出点P坐标．

25. 已知ABC中，∠ABC＝∠ACB，D为线段CB上一点（不与C、B重合），点E为射线CA上一点，∠ADE＝∠AED，设∠BAD＝α，∠CDE＝β．
（1）如图1，
①若∠BAC＝50°，∠DAE＝36°，则α＝　 　，β＝　 　；
②写出α与β的数量关系，并说明理由；
（2）如图2，当E点在CA的延长线上时，其它条件不变，写出α与β的数量关系，并说明理由．

26. 已知，在平面直角坐标系中，AB⊥x轴于点B，点A(a，b)满足+|b﹣3|＝0，平移线段AB使点A与原点重合，点B的对应点为点C．
（1）a＝　 　，b＝　 　，点C坐标为　 　；
（2）如图1，点D(m，n)射线CB上一个动点．
①连接OD，利用OBC，OBD，OCD的面积关系，可以得到m、n满足一个固定的关系式，请写出这个关系式：　 　；
②过点A作直线1∥x轴，在l上取点M，使得MA＝2，若CDM的面积为4，请直接写出点D的坐标　 　．
（3）如图2，以OB为边作∠BOG＝∠AOB，交线段BC于点G，E是线段OB上一动点，连接CE交OG于点F，当点E在线段OB上运动过程中，的值是否发生变化？若变化请说明理由，若不变，求出其值．

27. 设a是4+的整数部分，b是4﹣的小数部分，则a＝ _____，b＝_____．
28. 在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步沿x轴向右走1个单位长度，第2步向右走2个单位长度，第3步向上走1个单位长度，第4步向右走1个单位长度，…，依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位长度：当n被3除，余数为1时，则向右走1个单位长度：当n被3除，余数为2时，则向右走2个单位长度，当走完第6步时，棋子所处位置的坐标是　 　，当走完第7步时，棋子所处位置的坐标是　 　，当走完第2021步时，棋子所处位置的坐标是　 　．
29. 长度为20厘米的木棍，截成三段，每段长度为整数厘米，请写出一种可以构成三角形的截法，此时三段长度分别为　 　，能构成三角形的截法共有　 　种，（只考虑三段木棍的长度）
30. 如图，对于平面直角坐标系xOy中的任意两点A(xA，yA)，B(xB，yB)，它们之间的曼哈顿距离定义如下：|AB|1＝|xA﹣xB|+|yA﹣yB|．已知O为坐标原点，点P(4，﹣5)，Q(﹣2，4)．
（1）|OP|1＝　 　，|PQ|1＝　 　．
（2）已知点T(t，1)，其中t为任意实数．
①若|TP|1＝10，求t的值．
②若P、Q、T三点在曼哈顿距离下是等腰三角形，请直接写出t的值．


2021北京四中初一（下）期中数学
参考答案
一、选择题
1. 【答案】C
【解析】
【分析】直接根据对顶角的概念判断即可得到答案．
【详解】解：A、不符合对顶角概念，不符合题意；
B、不符合对顶角概念，不符合题意；
C、符合对顶角概念，符合题意；
D、不符合对顶角概念，不符合题意．
故选：C．
【点睛】此题考查的是对顶角的概念，掌握其概念是解决此题关键．
2.【答案】D
【解析】
【分析】先计算的值为3，再利用平方根的定义即可得到结果．
【详解】∵=3，
∴的平方根是±．
故选D．
【点睛】此题考查了平方根，以及算术平方根，解决本题的关键是先求得的值.
3. 【答案】B
【解析】
【分析】根据第二象限的点的横坐标是负数，纵坐标是正数解答．
【详解】解：点（-4，2）所在的象限是第二象限．
故选：B．
【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
4. 【答案】D
【解析】
【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．
【详解】解：A、3+4＜8，不能构成三角形；
B、5+6=11，不能构成三角形；
C、4+4=8，不能构成三角形；
D、8+8＞8，能构成三角形．
故选：D．
【点睛】此题主要考查了三角形三边关系，根据第三边的范围是：大于已知的两边的差，而小于两边的和是解决问题的关键．
5. 【答案】C
【解析】
【分析】根据多边形的外角和定理即可求解判断．
【详解】解：∵任何多边形的外角和都是360°，
∴多边形的边数由3增加到2021时，其外角和的度数不变，
故选：C．
【点睛】此题考查多边形的外角和，熟记多边形的外角和是360度，并不随边数的变化而变化是解题的关键．
6. 【答案】B
【解析】
【分析】利用对顶角的定义、平行线的性质等知识分别判断后即可确定正确的选项．
【详解】解：A、相等的两个角不一定是对顶角，故原命题错误，是假命题，不符合题意；
B、过直线外一点有且只有一条直线与已知直线平行，正确，是真命题，符合题意；
C、两条平行线被第三条直线所截，内错角相等，故原命题错误，是假命题，不符合题意；
D、在同一平面内，垂直于同一条直线的两条直线互相平行，故原命题错误，是假命题，不符合题意，
故选：B．
【点睛】本题考查了命题与定理的知识，解题的关键是了解对顶角的定义、平行线的性质等知识，难度不大．
7. 【答案】C
【解析】
【分析】利用平行线的判定方法分别判断即可得出答案．
【详解】解：①当∠DCA=∠CAF时，AB∥CD，符合题意；
②当∠C=∠EDB时，AC∥DB，不合题意；
③当∠BAC+∠C=180°时，AB∥CD，符合题意；
④当∠GDE+∠B=180°时，
又∵∠GDE+∠EDB=180°，
∴∠B=∠EDB，
∴AB∥CD，符合题意；
故选：C．
【点睛】本题考查的是平行线的判定，内错角相等，两直线平行；同位角相等，两直线平行；同旁内角互补，两直线平行，正确掌握平行线的判定是解题关键．．
8. 【答案】C
【解析】
【分析】直接利用立方根以及算术平方根、无理数的定义分析得出答案．
【详解】解：由题意可得：64的立方根为4，4的算术平方根是2，2的算术平方根是，
即．
故选：C．
【点睛】此题主要考查了立方根以及算术平方根、无理数的定义，正确掌握相关定义是解题关键．
9. 【答案】D
【解析】
【详解】圆心由A(－2，1)移到O(0，0)，向右平移2个单位，向下平移1个单位，因此P(m，n)的对应点P′的坐标为(m＋2，n－1)．
10. 【答案】B
【解析】
【分析】过作，过作，利用平行线的性质解答即可．
【详解】解：过作，过作，
，
，
，，
，，
，，，
，
．
故选：B．

【点睛】此题考查平行线的性质，关键是作出辅助线，利用平行线的性质解答．
二、填空题
11.【答案】如（答案不唯一）
【解析】
【分析】首先2可以写成，由于开方开不尽的数是无理数，由此即可求解．
【详解】解：∵2=，
∴大于2的无理数须使被开方数大于4即可，如（答案不唯一）．
【点睛】本题考查无理数定义及比较大小．熟练掌握无理数的定义是解题的关键．
12. 【答案】540°
【解析】
【分析】根据多边形的内角和是（n-2）•180°，代入计算即可．
【详解】解：根据题意得：（5-2）•180°=540°，
故答案为：540°．
【点睛】本题考查的是多边形的内角和的计算，掌握多边形的内角和可以表示成（n-2）•180°是解题的关键．
13. 【答案】（9，-1）
【解析】
【分析】根据表示西桥的点的坐标为，表示中堤桥的点的坐标为建立平面直角坐标系，确定坐标原点的位置，进而可确定表示留春园的点的坐标．
【详解】解：根据题意可建立如下所示平面直角坐标系，

则表示留春园的点的坐标为，
故答案为．
【点睛】此题考查坐标确定位置，解题的关键就是确定坐标原点和x，y轴的位置．
14. 【答案】20
【解析】
【详解】分析：首先根据平行线的性质得出∠5的度数，然后根据三角形外角的性质得出答案．
详解：∵直尺的两边平行， ∴∠5=∠2=50°，
根据三角形外角的性质可得：∠1+∠3=∠5=50°， ∴∠3=50°－30°=20°．

点睛：本题主要考查的是平行线的性质以及三角形外角的性质，属于基础题型．解决这个问题时要综合应用两个性质．
15. 【答案】20或22
【解析】
【分析】由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析．
【详解】①6是腰长时，三角形的三边分别为6、6、8，
能组成三角形，周长=6+6+8=20，
②6是底边长时，三角形的三边分别为6、8、8，
能组成三角形，周长=6+8+8=22，
综上所述，这个等腰三角形的周长是20或22，
故答案为20或22．
【点睛】本题考查了等腰三角形的性质，三角形三边关系，解题的关键在于分情况讨论并利用三角形的三边关系判断是否能组成三角形．
16. 【答案】三
【解析】
【分析】根据题意作出平面直角坐标系，根据图象可以直接得到答案．
【详解】解：如图，

∵点A的坐标为（-2，4），点B的坐标为（4，-2），
∴点A位于第二象限，点B位于第四象限，
∴点C位于第三象限．
故答案是：三．
【点睛】本题考查了坐标与图形性质，解题时，利用了“数形结合”的数学思想，比较直观．
17. 【答案】4
【解析】
【分析】根据图象中的信息即可得到结论．
【详解】由图象中的信息可知，
1月份每斤的利润=10.8-10=0.8元，
2月份每斤的利润=9-7=2元，
3月份每斤的利润＝7.5﹣4.5＝3元，
4月份每斤的利润＝6﹣2.5＝3.5元，
5月份每斤的利润＝4.5﹣2＝2.5元，
6月份每斤的利润＝3﹣1.8＝1.2元，
7月份每斤的利润＝1.5﹣1.2＝0.3元，
故出售该种水果每斤利润最大的月份是4月份，
故答案为4
【点睛】本题考查了象形统计图，有理数大小的比较，正确的把握图象中的信息，理解利润＝售价﹣进价是解题的关键．
18. 【答案】①③④
【解析】
【分析】估计无理数的大小即可逐个排除．
【详解】解：．
．
，故①正确．
当时．
．
．
整数有：708，709，710，711，712共5个．故②错误．
设小于26的两个正数分别是，，则．

．故③正确．
．
正方形边长为26.4，那么这个正方形的面积是696.96．故④正确．
故答案为：①③④．
【点睛】本题考查平方根与平方，平方差公式，通过表格数据对平方根进行估计是求解本题的关键．
三、解答题
19. 【答案】3
【解析】
【分析】根据立方根与平方根的意义以及绝对值的意义计算．
【详解】解：
=
=
【点睛】本题考查了实数混合运算运算，正确理解平方根与立方根的意义是解题的关键．
20. 【答案】（1）；（2）
【解析】
【分析】（1）根据立方根的意义进行计算．
（2）根据平方根的意义进行计算．
【详解】解：（1），
，
．
（2），
，
，
．
【点睛】此题考查了立方根平方根的意义．正确理解平方根立方根的意义是解题的关键．
21. 【答案】垂直定义；AF，DE，同位角相等，两直线平行；两直线平行，同位角相等；内错角相等，两直线平行
【解析】
【分析】根据平行线的判定与性质即可完成推理填空．
【详解】证明：∵AF⊥CE，
∴∠CGF=90° （垂直定义），
∵∠1=∠D（已知），
∴AF∥DE（同位角相等，两直线平行），
∴∠4=∠CGF=90°（两直线平行，同位角相等），
∵∠2+∠3+∠4=180°（平角的定义），
∴∠2+∠3=90°．
∵∠2与∠C互余（已知），
∴∠2+∠C=90°（互余的定义），
∴∠C=∠3（同角的余角相等），
∴AB∥CD （内错角相等，两直线平行）．
故答案为：垂直定义；AF，DE，同位角相等，两直线平行；两直线平行，同位角相等；内错角相等，两直线平行．
【点睛】本题考查了平行线的判定与性质，解决本题的关键是熟练掌握平行线的判定与性质．
22. 【答案】（1）（-9，0）；（2）（3，4）
【解析】
【分析】（1）根据x轴上点的纵坐标为0列方程求出a的值，再求解即可；
（2）根据平行于y轴的直线上的点的纵坐标相同列方程求出a的值，再求解即可．
【详解】解：（1）∵点A（3a-6，a+1）在x轴上，
∴a+1=0，
解得a=-1，
∴3a-6=-3-6=-9，
∴点A的坐标为（-9，0）；
（2）∵点A在过点P（3，-2），且与y轴平行直线上，
∴3a-6=3，
解得a=3，
∴a+1=3+1=4，
∴点A的坐标为（3，4）．
【点睛】本题考查了点的坐标，熟练掌握坐标轴上点的坐标特征以及平行于坐标轴的直线上的点的坐标特征是解题的关键．
23. 【答案】（1）见解析；（2）22°；（3），证明见解析
【解析】
【分析】（1）根据题意画出图形即可；
（2）在中，利用三角形内角和定理可求出的度数，结合角平分线的定义可求出的度数，由是边上的高，可求出的度数，再结合即可求出结论；
（3）根据题意可以用和表示出和，从而可以得到与的关系．
【详解】解：（1）如图，

（2）在中，，，
，
平分，
，
是边上的高，
，
，
．
（3），
理由：在中，，分别是的高和角平分线，
，，，
．
【点睛】本题考查三角形内角和定理，熟练掌握角的平分线的性质、直角三角形的性质是解题的关键．
24. 【答案】（1）；（2）画图见解析，3；（3）或
【解析】
【分析】（1）利用直角坐标系可直接写出点坐标；
（2）分别作出，，的对应点，，即可得到△，用一个矩形的面积分别减去三个三角形的面积去计算△的面积；
（3）设．利用三角形面积关系构建方程求解即可．
【详解】解：（1）点的坐标为，
故答案为：；
（2）如图，△即为所求．

△的面积：；
（3）设．

，，将向右平移6个单位，向下平移1个单位，对应得到△，
，，
∴△的面积，
解得：或7，
或．
【点睛】本题考查作图平移变换，三角形的面积等知识，解题的关键是熟练掌握平移变换的性质，属于中考常考题型．
25. 【答案】（1）①14°，7°；②α＝2β，理由见解析；（2）2β＝180°+α，理由见解析
【解析】
【分析】（1）①直接求α的度数，根据三角形的内角和与等腰三角形的性质求∠ACB和∠AED的度数，再根据外角定理求出β的度数；
②设∠BAC＝x°，∠DAE＝y°，则α＝x°-y°，同理求出∠ACB=和∠AED=，利用外角定理得：β＝∠AED﹣∠ACB，代入可得结论；
（2）设∠BAC＝x°，∠DAE＝y°，根据图形先表示α＝x°-（180°-y°）＝x°-180°+y°，同理得∠ACB和∠AED的度数，在△EDC中利用外角定理列式可得结论．
【详解】解：（1）如图（1），
①∵∠BAC＝50°，∠ACB＝∠ABC，
∴∠ABC＝∠ACB==65°，
∵∠DAE＝36°，∠ADE＝∠AED，
∴∠ADE＝∠AED＝72°，
∵∠AED是△DEC的一个外角，
∴∠AED＝∠EDC+∠ACB，
∴∠EDC＝∠AED-∠ACB＝72°-65°＝7°，
即β＝7°，
α＝∠BAC-∠DAE＝50°-36°＝14°；
故答案为：14°，7°；
②α＝2β，理由：
设∠BAC＝x°，∠DAE＝y°，则α＝x°-y°，
∵∠ACB＝∠ABC，
∴∠ACB=，
∵∠ADE＝∠AED，
∴∠AED=，
∴β＝∠AED﹣∠ACB=，
∴α＝2β；
（2）如图（2），2β＝180°+α，理由是：
设∠BAC＝x°，∠DAE＝y°，
α＝x°-（180°-y°）＝x°-180°+y°，
∵∠ACB＝∠ABC，
∴∠ACB=，
∵∠ADE＝∠AED，
∴∠AED=，
∴∠EDB是△EDC的一个外角，
∴∠EDB＝∠AED+∠ACB，
∴180°-β=，
∴2β＝x°+y°，
∴2β＝180°+α．
【点睛】本题是三角形的综合题，难度适中，考查了三角形的内角和、等腰三角形的性质、外角定理；本题的解题思路为：①先表示两个等腰三角形两个底角的度数，②利用外角定理列式，将α、β代入即可．
26. 【答案】（1）6，3，（0，-3）；（2）①m-2n＝6；②（2，-2）或（4，-1）；（3）不变，理由见解析
【解析】
【分析】（1）利用非负数的性质求解即可．
（2）①如图1，过点分别作轴于点，轴于点，连接，利用面积法求解即可．②如图中，设直线交轴于，连接，，．分两种情形：当点在点的左侧时，设，根据，构建方程求解，当点在点的右侧时，同法可得．
（3）的值不变，值为2．利用平行线的性质，三角形的外角的性质证明即可．
【详解】解：（1），
，，
，，
，且在轴负半轴上，
，
故答案为：6，3，．
（2）①如图1-1，过点分别作轴于点，轴于点，连接．

轴于点，且点，，三点的坐标分别为：，，，
，，，，
，
又


，
，
，
、满足的关系式为．
故答案为：．
②如图中，设直线交轴于，连接，，．

当点在点的左侧时，设，
，
，
解得，
，
当点在点的右侧时，同法可得，
综上所述，满足条件的点的坐标为或．
故答案为：或．
（3）的值不变，值为2．理由如下：
线段是由线段平移得到，
，
，
又，
，
根据三角形外角性质，可得，，


，
．
【点睛】本题属于几何变换综合题，主要考查了非负数，坐标与图形，平行线的性质以及平移的性质，解决问题的关键是作辅助线，运用面积法，角的和差关系以及平行线的性质进行求解．
27. 【答案】6，
【解析】
【分析】估算出的范围，从而得到4+和4-的范围，可得a，b的值．
【详解】解：∵，
∴，
∴，，
∴，
∴a=6，b==，
故答案为：6，．
【点睛】本题主要考查了估算无理数的大小，根据题意进行计算是解决本题的关键．
28. 【答案】A6（6，2），A7（7，2），（2021，673）
【解析】
【分析】设走完第n步，棋子的坐标用An来表示．列出部分A点坐标，发现规律“A3n（3n，n），A3n+1（3n+1，n），A3n+2（3n+3，n）”，根据该规律即可解决问题．
【详解】解：设走完第n步，棋子的坐标用An来表示．
观察，发现规律：A0（0，0），A1（1，0），A2（3，0），A3（3，1），A4（4，1），A5（6，1），A6（6，2），A7（7，2），…，
…，
∴A3n（3n，n），A3n+1（3n+1，n），A3n+2（3n+3，n）．
∵2021=673×3+2，
∴A2021（2021，673）．
故答案为：A6（6，2），A7（7，2），（2021，673）．
【点睛】本题考查了规律型中的点的坐标，解题的关键是发现规律“A3n（3n，n），A3n+1（3n+1，n），A3n+2（3n+3，n）”．本题属于基础题，难度不大，解决该题型题目时，根据棋子的运动情况，罗列出部分A点的坐标，根据坐标的变化发现规律是关键．
29. 【答案】9厘米，9厘米，2厘米（答案不唯一）；8
【解析】
【分析】已知三角形的周长，分别假设三角形的最长边，从而利用三角形三边关系进行验证即可求得不同的截法．
【详解】解：∵木棍的长度为20厘米，即三角形的周长为20厘米，
∴①当三角形的最长边为9厘米时，有4种截法，分别是：9厘米，9厘米，2厘米；9厘米，8厘米，3厘米；9厘米，7厘米，4厘米；9厘米，6厘米，5厘米；
②当三角形的最长边为8厘米时，有3种截法，分别是：8厘米，8厘米，4厘米；8厘米，7厘米，5厘米；8厘米，6厘米，6厘米；
③当三角形的最长边为7厘米时，有1种截法，是：7厘米，7厘米，6厘米；
∴能构成三角形的截法共有4+3+1=8种．
故答案为：9厘米，9厘米，2厘米（答案不唯一）；8．
【点睛】此题主要考查学生对三角形三边关系的理解及运用能力，注意不能构成三角形的情况一定要排除．
30. 【答案】（1）9，15；（2）①8或0；②-5或13或10或-14或2.5
【解析】
【分析】（1）根据曼哈顿距离的定义求解即可．
（2）①根据曼哈顿距离的定义构建方程求解即可．
②由题意，|TP|1=|PQ|1或|TQ|1=|PQ|1或|TP|1=|TQ|1，分这3种情况得到关于t的方程，解方程即可．
【详解】解：（1）由题意，|OP|1=|4-0|+|-5-0|=9，|PQ|1=|4+2|+|-5-4|=15．
故答案为9，15．
（2）①由题意：|t-4|+|1+5|=10，
当t＞4时，t=8，
当t＜4时，t=0，
综上所述，t的值为8或0．
②由题意，|TP|1=|PQ|1或|TQ|1=|PQ|1或|TP|1=|TQ|1，
当|TP|1=|PQ|1时，|t-4|+|1+5|=15，
解得t=-5或13；
当|TQ|1=|PQ|1时，|t+2|+|1-4|=15，
解得t=10或-14，
|TP|1=|TQ|1时，|t-4|+|1+5|=|t+2|+|1-4|，
解得t=2.5，
综上所述，t的值为-5或13或10或-14或2.5．
【点睛】本题考查了新定义，绝对值方程，分类讨论是解题的关键．