2021北京重点校初三（上）期中数学汇编：图形的旋转

2021北京重点校初三（上）期中数学汇编

图形的旋转

一、单选题

1．（2021·北京八中九年级期中）如图，香港特别行政区标志紫荆花图案绕中心旋转°后能与原来的图案互相重合，则的最小值为（       ）

A．45 B．60 C．72 D．144

2．（2021·北京八十中九年级期中）如图，△ABC经过变换得到△AB'C'，其中△ABC绕点A逆时针旋转60°的是（　　）

A． B．

C． D．

3．（2021·北京·北师大实验中学九年级期中）如图，△AOB绕点O逆时针旋转65°得到△COD，若∠COD＝30°，则∠BOC的度数是（　　）

A．30° B．35° C．45° D．60°

二、填空题

4．（2021·北京八十中九年级期中）在平面直角坐标系中，把点A（1，﹣4）绕坐标原点逆时针旋转90°，得到点B，则点B的坐标为 ___．

三、解答题

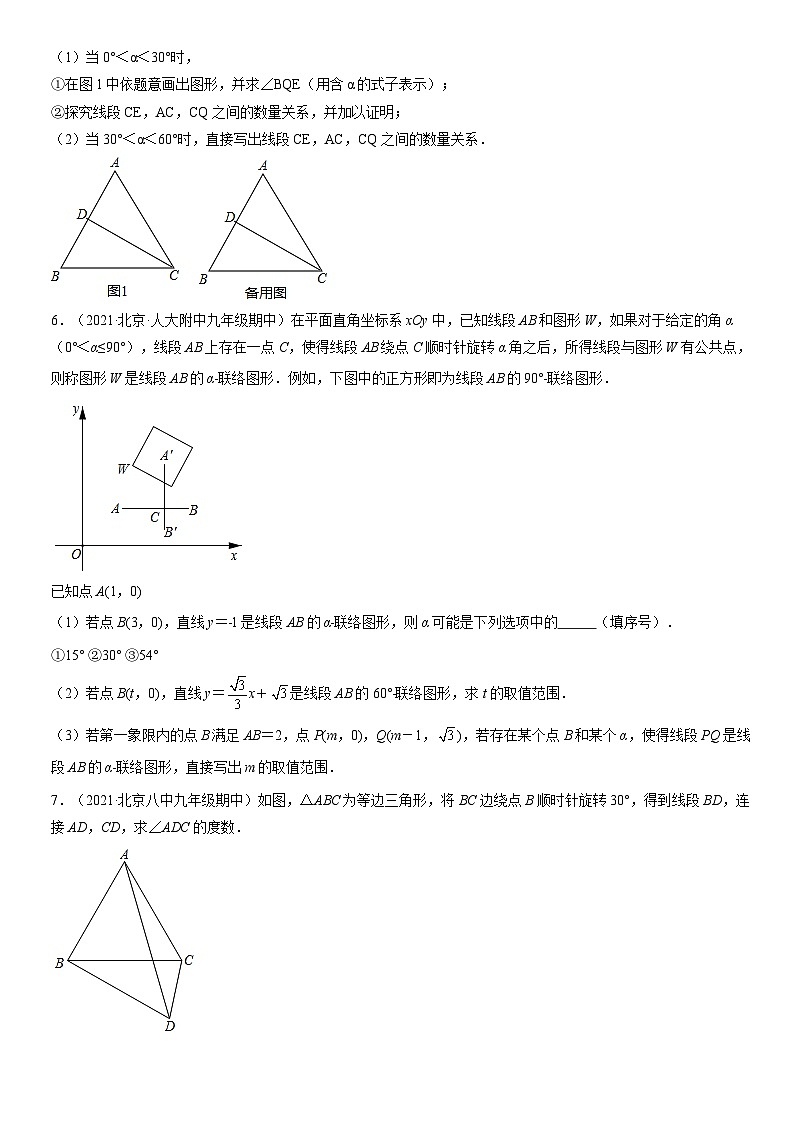
5．（2021·北京一七一中九年级期中）如图1，在等边△ABC中，CD为中线，点Q在线段CD上运动，将线段QA绕点Q顺时针旋转，使得点A的对应点E落在射线BC上，连接BQ，设∠DAQ=α（0°＜α＜60°且α≠30°）．

（1）当0°＜α＜30°时，

①在图1中依题意画出图形，并求∠BQE（用含α的式子表示）；

②探究线段CE，AC，CQ之间的数量关系，并加以证明；

（2）当30°＜α＜60°时，直接写出线段CE，AC，CQ之间的数量关系．

6．（2021·北京·人大附中九年级期中）在平面直角坐标系xOy中，已知线段AB和图形W，如果对于给定的角α（0°＜α≤90°），线段AB上存在一点C，使得线段AB绕点C顺时针旋转α角之后，所得线段与图形W有公共点，则称图形W是线段AB的α﹣联络图形．例如，下图中的正方形即为线段AB的90°﹣联络图形．

已知点A(1，0)

（1）若点B(3，0)，直线y＝﹣1是线段AB的α﹣联络图形，则α可能是下列选项中的           （填序号）．

①15° ②30° ③54°

（2）若点B(t，0)，直线y＝x＋是线段AB的60°﹣联络图形，求t的取值范围．

（3）若第一象限内的点B满足AB＝2，点P(m，0)，Q(m－1，)，若存在某个点B和某个α，使得线段PQ是线段AB的α﹣联络图形，直接写出m的取值范围．

7．（2021·北京八中九年级期中）如图，△ABC为等边三角形，将BC边绕点B顺时针旋转30°，得到线段BD，连接AD，CD，求∠ADC的度数．

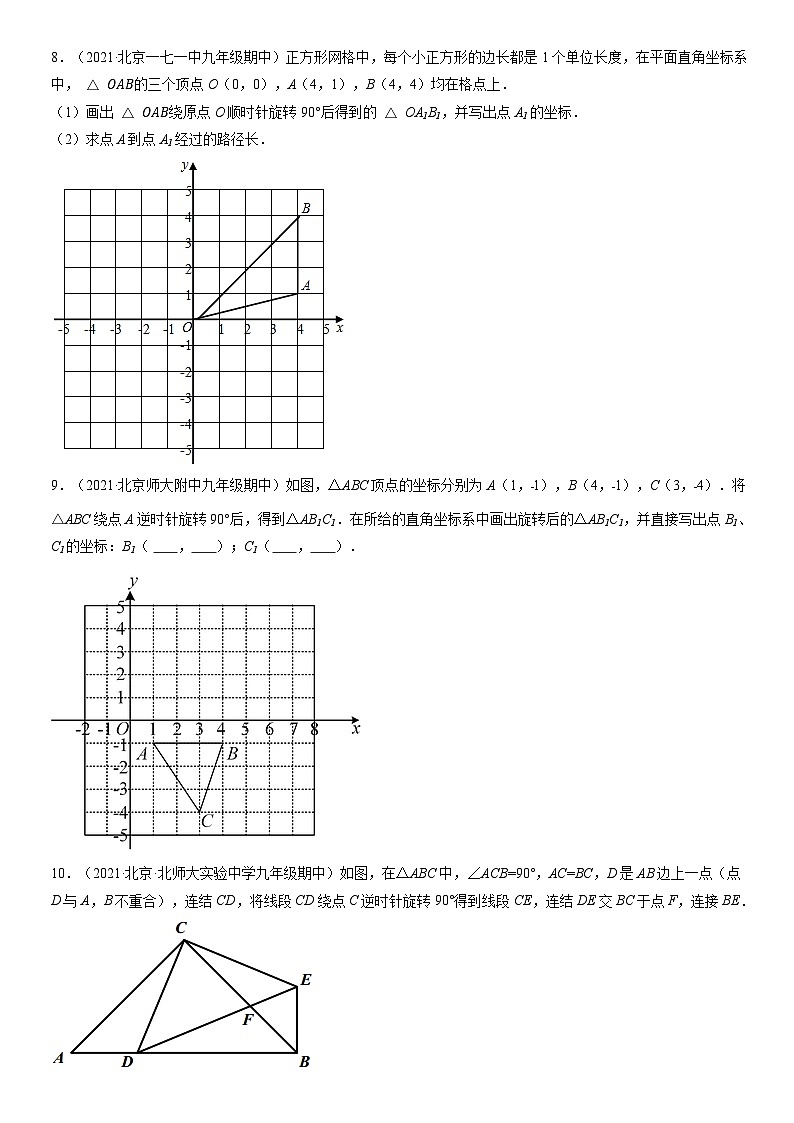
8．（2021·北京一七一中九年级期中）正方形网格中，每个小正方形的边长都是1个单位长度，在平面直角坐标系中，的三个顶点O（0，0），A（4，1），B（4，4）均在格点上．

（1）画出绕原点O顺时针旋转90°后得到的OA1B1，并写出点A1的坐标．

（2）求点A到点A1经过的路径长．

9．（2021·北京师大附中九年级期中）如图，△ABC顶点的坐标分别为A（1，﹣1），B（4，﹣1），C（3，﹣4）．将△ABC绕点A逆时针旋转90°后，得到△AB1C1．在所给的直角坐标系中画出旋转后的△AB1C1，并直接写出点B1、C1的坐标：B1（        ，       ）；C1（       ，       ）．

10．（2021·北京·北师大实验中学九年级期中）如图，在△ABC中，∠ACB=90°，AC=BC，D是AB边上一点（点D与A，B不重合），连结CD，将线段CD绕点C逆时针旋转90°得到线段CE，连结DE交BC于点F，连接BE．

(1)求证：△ACD≌△BCE；

(2)当∠BDE=25°时，求∠BEF的度数．

参考答案

1．C

【分析】

该图形被平分成五部分，因而每部分被分成的圆心角是，并且圆具有旋转不变性，因而旋转的整数倍，就可以与自身重合.

【详解】

该图形被平分成五部分，旋转的整数倍，就可以与自身重合，

故的最小值为.

故选：.

【点睛】

本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角.

2．D

【分析】

分别确定每个选项中的各组对应点，各组对应线段，观察变换前后的位置特征结合轴对称变换与旋转变换的特征逐一分析，从而可得答案.

【详解】

解：选项A体现的是把△ABC绕点A逆时针旋转90°得到 故A不符合题意；

选项B体现的是把△ABC沿某条直线对折得到 故B不符合题意；

选项C体现的是把△ABC沿某条直线对折得到 故C不符合题意；

选项D体现的是把△ABC绕点A逆时针旋转60°得到 故D符合题意；

故选D

【点睛】

本题考查的是轴对称变换，旋转变换，掌握轴对称变换与旋转变换的特征是解题的关键.

3．B

【分析】

由旋转的性质可得∠AOC＝65°，由∠AOB＝30°，即可求∠BOC的度数．

【详解】

解：∵△AOB绕点O逆时针旋转65°得到△COD，

∴∠AOC＝65°，

∵∠AOB＝30°，

∴∠BOC＝∠AOC−∠AOB＝35°.

故选：B．

【点睛】

本题考查了旋转的性质，三角形内角和定理，熟练运用旋转的性质是本题的关键．

4．

【分析】

先作出符合题意的图形，过作轴于 过作轴于 再证明再利用全等三角形的性质可得答案.

【详解】

解：如图， 把点A（1，﹣4）绕坐标原点逆时针旋转90°，得到点B，

过作轴于 过作轴于

则

故答案为：

【点睛】

本题考查的是旋转的性质，图形与坐标，全等三角形的判定与性质，灵活运用以上知识解题是关键.

5．（1）图形见解析；∠BQE=60°+2α；（2）CE+AC=CQ；证明见解析；（3）AC-CE=CQ．

【分析】

（1）①先根据等边三角形的性质的QA=QB，进而得出QB=QE，最后用三角形的内角和定理即可得出结论；

②延长CA到点F，使得AF=CE，连接QF，作QH⊥AC于点H．先判断出△QAF≌△QEC，得出QF=QC，再判断出△QCF是底角为30度的等腰三角形，再构造出直角三角形即可得出结论；

（2）同②的方法即可得出结论．

【详解】

（1）当0°＜α＜30°时，

①画出的图形如图1所示，

∵△ABC为等边三角形，

∴∠ABC=60°．

∵CD为等边三角形的中线，

∴CD是AB的垂直平分线，

∵Q为线段CD上的点，

∴QA=QB．

∵∠DAQ=α，

∴∠ABQ=∠DAQ=α，∠QBE=60°-α．

∵线段QE为线段QA绕点Q顺时针旋转所得，

∴QE=QA．

∴QB=QE．

∴∠QEB=∠QBE=60°-α，

∴∠BQE=180°-2∠QBE=180°-2（60°-α）=60°+2α；

②CE+AC=CQ；证明：

如图2，延长CA到点F，使得AF=CE，连接QF，作QH⊥AC于点H．

∵∠BQE=60°+2α，点E在BC上，

∴∠QEC=∠BQE+∠QBE=（60°+2α）+（ 60°-α）=120°+α．

∵点F在CA的延长线上，∠DAQ=α，

∴∠QAF=∠BAF+∠DAQ=120°+α．

∴∠QAF=∠QEC．

又∵AF=CE，QA=QE，

∴△QAF≌△QEC．

∴QF=QC．

∵QH⊥AC于点H，

∴FH=CH，CF=2CH．

∵在等边三角形ABC中，CD为中线，

点Q在CD上，

∴∠ACQ=∠ACB=30°，

即△QCF为底角为30°的等腰三角形．

∴CH＝CQ•cos∠HCQ＝CQ•cos30°＝CQ．

∴CE+AC=AF+AC=CF=2CH＝CQ．

（2）如图3，当30°＜α＜60°时，

在AC上取一点F使AF=CE，

∵△ABC为等边三角形，

∴∠ABC=60°．

∵CD为等边三角形的中线，

∵Q为线段CD上的点，

∴CD是AB的垂直平分线，

由等边三角形的对称性得QA=QB．

∵∠DAQ=α，

∴∠ABQ=∠DAQ=α，∠QBE=60°-α．

∵线段QE为线段QA绕点Q顺时针旋转所得，

∴QE=QA．

∴QB=QE．

∴∠QEB=∠QBE=60°-α=∠QAF，

又∵AF=CE，QA=QE，

∴△QAF≌△QEC．

∴QF=QC．

∵QH⊥AC于点H，

∴FH=CH，CF=2CH．

∵在等边三角形ABC中，CD为中线，点Q在CD上，

∴∠ACQ=∠ACB=30°，

即△QCF为底角为30°的等腰三角形．

∴CH＝CQ•cos∠HCQ＝CQ•cos30°＝CQ．

∴AC-CE=AC-AF=CF=2CH＝CQ．

【点睛】

此题是几何变换综合题，主要考查了等边三角形的性质，三角形的内角和定理，全等三角形的判定和性质，等腰三角形的判定和性质，锐角三角函数，作出辅助线构造出全等三角形是解本题的关键．

6．（1）②③；（2）；（3）

【分析】

（1）将线段AB绕点A逆时针旋转，使点B落到直线上的C点，过点C作于点D，求出AB，CD的长度，根据直角三角形的性质得；

（2）根据一次函数的性质得，，则，，在中，根据正切得，连接AC，在中，根据正切得，则，根据得，即；

（3）当时，过点Q作于点C，在中，根据正切得，在中，，则，即，当点B在y轴上时，在中，根据余弦得，所以当m=1时，线段AB在直线PQ上，即可得．

【详解】

解：（1）如图所示，将线段AB绕点A逆时针旋转，使点B落到直线上的C点，过点C作于点D，

∵A（1，0），B（3，0），

∴，，

∴，

∴在中，，

如下图，将线段AB绕AB中点逆时针旋转90°，

此时点B刚好落到直线y=-1上的B'点，

即若直线y=- 1是线段AB的α-联络图形，α最大取值为90°，

∴30°≤α≤90°

故答案为：②③；

（2）在中，当时，，

当时，，

，

∴，，

∴，，

∵在中，，

∴，

如图所示，连接AC，

∵A（1，0），

∴OA=1，

∵在中，，

∴，

∴，

∴，

，

即，

∴；

（3）如图所示，当时，过点Q作于点C，

∵，，

∴，，

∵在中，，

∴，

∵在中，，

∴，

∴，

如图所示，当点B在y轴上时，

∵在中，，

∴，

∴当m=1时，线段AB在直线PQ上，

又∵点B在第一象限，

∴m的取值范围是：．

【点睛】

本题考查了旋转，直角三角形的性质，一次函数的性质，正弦，余弦，正切，解题的关键是掌握并灵活运用这些知识点．

7．30°

【分析】

首先证明∠ABD＝90°，求出∠BDC，∠ADB即可解决问题．

【详解】

解：∵△ABC为等边三角形，

∴AB＝BC，∠ABC＝60°．

根据题意可知BD＝BC，∠DBC＝30°．

∴AB＝BD=BC，∠ABD＝90°，

∴∠BDC＝75°，∠BDA＝45°

∴∠ADC＝∠BDC ﹣∠BDA＝30°．

【点睛】

本题考查等边三角形的性质、旋转的性质、等腰三角形的性质，熟练掌握相关知识点性质是解答的关键．

8．（1）作图见解析，点的坐标为；（2）

【分析】

（1）将点、分别绕原点顺时针旋转后得到其对应点，再与点首尾顺次连接即可；

（2）先求出线段的长，再根据扇形的弧长公式结合求解即可．

【详解】

解：（1）如图所示，即为所求．

其中点的坐标为；

（2），，

点A到点A1经过的路径长为．

【点睛】

本题主要考查作图—旋转变换，解题的关键是掌握旋转变换的定义与性质及扇形弧长公式．

9．画图见解析；B1（1，2）；C1（4，1）．

【分析】

图形绕点A逆时针旋转90°，将AB，AC逆时针旋转90°，得到，连接， 利用网格特点和旋转的性质得出点B1、C1的坐标，从而得到△AB1C1．

【详解】

如图所示，△AB1C1为所作，B1点的坐标为（1，2），C1点的坐标为（4，1）．

故答案为（1，2），（4，1）．

【点睛】

本题考察了绕某点画旋转图形以及求点坐标，首先找到旋转的点，根据旋转角度和网格特征，即可得到对应坐标点．

10．(1)见解析；

(2)∠BEF=65°

【分析】

（1）由旋转的性质可得CD=CE，∠DCE=90°=∠ACB，由“SAS”可证△ACD≌△BCE，可得BE=AD，∠CBE=∠CAD=45°，可得结论；

（2）由全等三角形的性质以及三角形内角和定理可求解．

(1)

证明：∵将线段CD绕点C按逆时针方向旋转90°得到线段CE，

∴CD=CE，∠DCE=90°=∠ACB，

∴∠ACD=∠BCE，

∵∠ACB=90°，AC=BC，

∴∠CAB=∠CBA=45°，

在△ACD和△BCE中，

，

∴△ACD≌△BCE（SAS）；

(2)

解：∵△ACD≌△BCE，

∴∠CBE=∠CAD=45°，

∴∠ABE=∠ABC+∠CBE=90°，

∵∠BDE=25°，

∴∠BEF=65°．

【点睛】

本题考查了旋转的性质，全等三角形的判定和性质，等腰三角形的性质，证明三角形全等是解题的关键．