2023年中考数学精选真题实战测试40 菱形 B

2023年中考数学精选真题实战测试40 菱形 B

一、单选题（每题3分，共30分）(共10题；共30分)

1．（3分）（2021·河南）关于菱形的性质，以下说法不正确的是（　　） 

A．四条边相等 B．对角线相等

C．对角线互相垂直 D．是轴对称图形

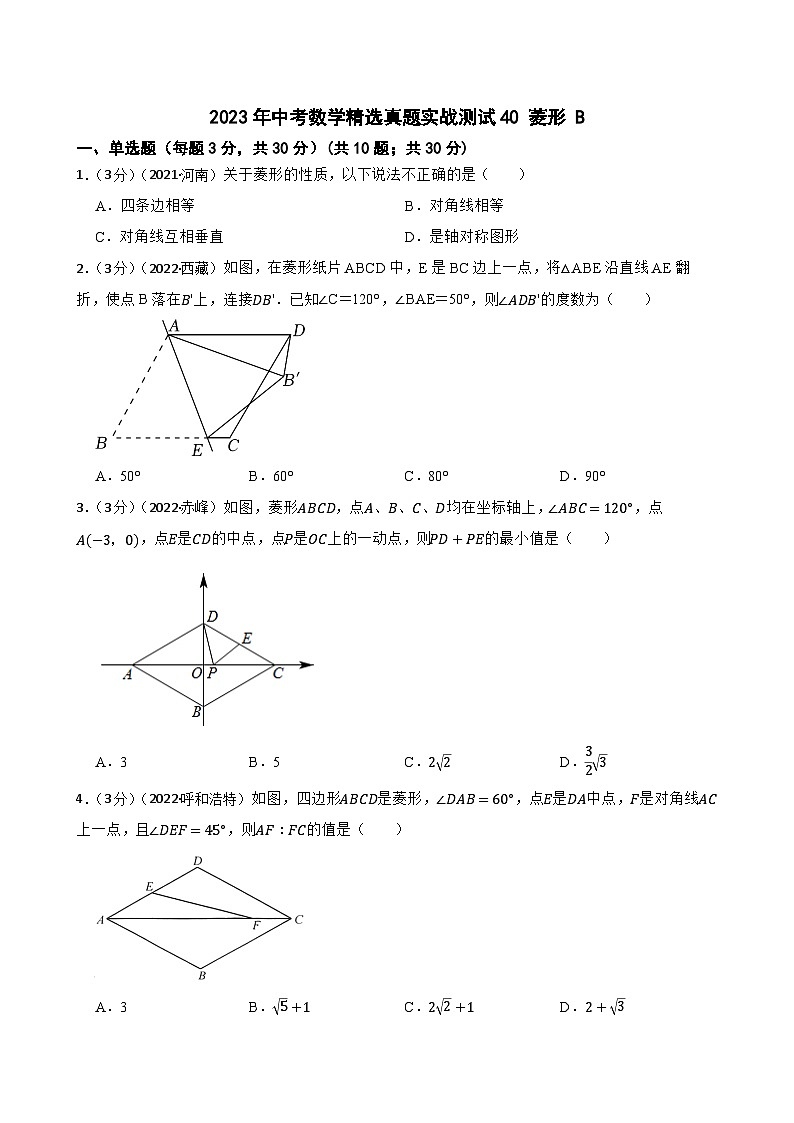
2．（3分）（2022·西藏）如图，在菱形纸片ABCD中，E是BC边上一点，将△ABE沿直线AE翻折，使点B落在上，连接．已知∠C＝120°，∠BAE＝50°，则的度数为（　　）

A．50° B．60° C．80° D．90°

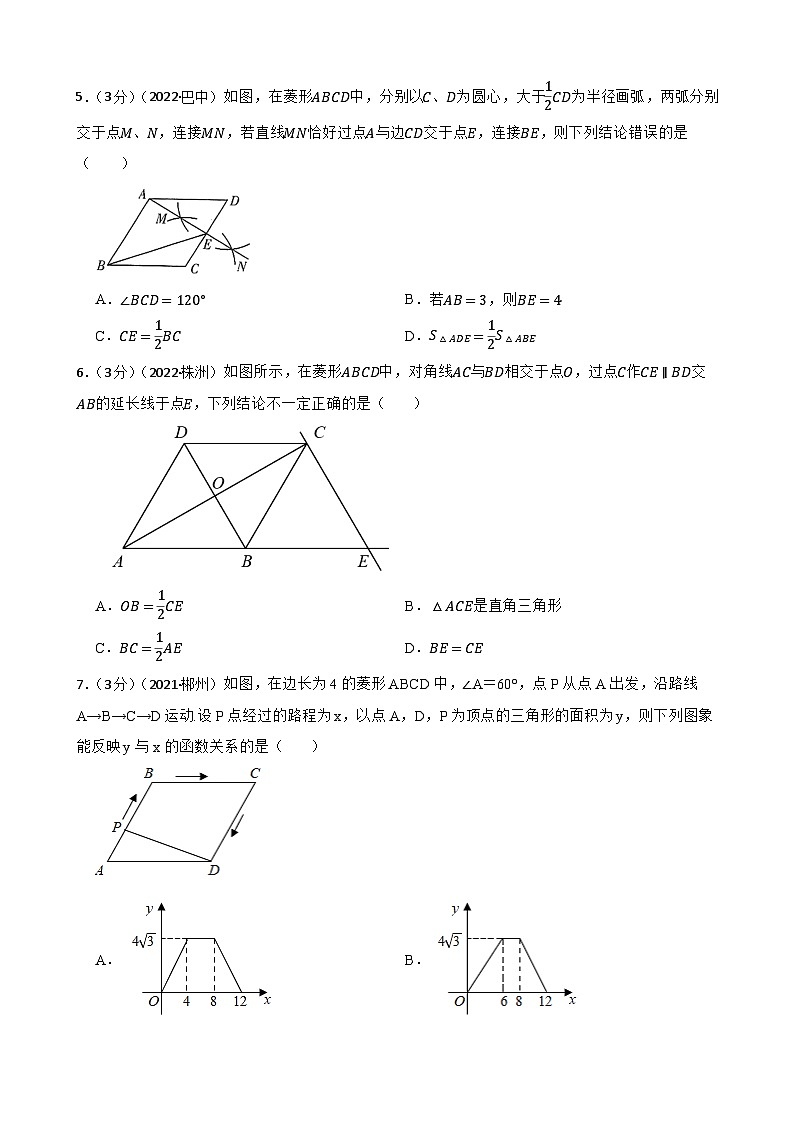
3．（3分）（2022·赤峰）如图，菱形，点、、、均在坐标轴上，，点，点是的中点，点是上的一动点，则的最小值是（　　）

A．3 B．5 C． D．

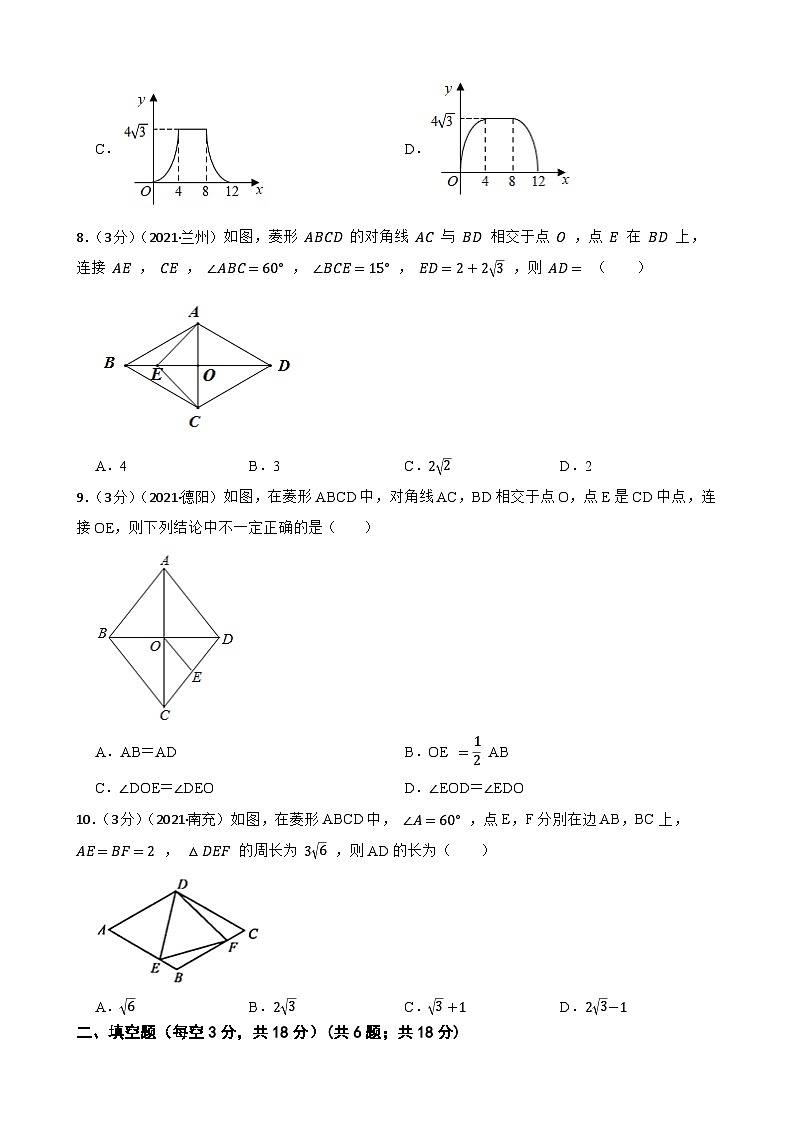
4．（3分）（2022·呼和浩特）如图，四边形是菱形，，点是中点，是对角线上一点，且，则的值是（　　）

A．3 B． C． D．

5．（3分）（2022·巴中）如图，在菱形中，分别以、为圆心，大于为半径画弧，两弧分别交于点、，连接，若直线恰好过点与边交于点，连接，则下列结论错误的是（　　）

A． B．若，则

C． D．

6．（3分）（2022·株洲）如图所示，在菱形中，对角线与相交于点，过点作交的延长线于点，下列结论不一定正确的是（　　）

A． B．是直角三角形

C． D．

7．（3分）（2021·郴州）如图，在边长为4的菱形ABCD中，∠A＝60°，点P从点A出发，沿路线A→B→C→D运动.设P点经过的路程为x，以点A，D，P为顶点的三角形的面积为y，则下列图象能反映y与x的函数关系的是（　　）

A． B．

C． D．

8．（3分）（2021·兰州）如图，菱形 的对角线 与 相交于点 ，点 在 上，连接 ， ， ， ， ，则 （　　） 

A．4 B．3 C． D．2

9．（3分）（2021·德阳）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E是CD中点，连接OE，则下列结论中不一定正确的是（　　） 

A．AB＝AD B．OE AB

C．∠DOE＝∠DEO D．∠EOD＝∠EDO

10．（3分）（2021·南充）如图，在菱形ABCD中， ，点E，F分別在边AB，BC上， ， 的周长为 ，则AD的长为（　　） 

A． B． C． D．

二、填空题（每空3分，共18分）(共6题；共18分)

11．（3分）（2022·常州）如图，将一个边长为的正方形活动框架（边框粗细忽略不计）扭动成四边形，对角线是两根橡皮筋，其拉伸长度达到时才会断裂.若，则橡皮筋　     　断裂（填“会”或“不会”，参考数据：）.

12．（3分）（2022·齐齐哈尔）如图，在四边形ABCD中，AC⊥BD，垂足为O，，要使四边形ABCD为菱形，应添加的条件是　                                                      　．（只需写出一个条件即可）

13．（3分）（2021·贵州）如图，BD是菱形ABCD的一条对角线，点E在BC的延长线上，若 ，则 的度数为　     　度. 

14．（3分）（2021·眉山）如图，在菱形 中， ，对角线 、 相交于点 ，点 在线段 上，且 ，点 为线段 上的一个动点，则 的最小值是　     　.

15．（3分）（2021·苏州）如图，四边形 为菱形， ，延长 到 ，在 内作射线 ，使得 ，过点 作 ，垂足为 ，若 ，则对角线 的长为　     　.（结果保留根号） 

16．（3分）（2022·陕西）如图，在菱形中，.若M、N分别是边上的动点，且，作，垂足分别为E、F，则的值为　     　.

三、解答题（共8题，共72分）(共8题；共72分)

17．（8分）（2022·长沙）如图，在中，对角线AC，BD相交于点O，.

（1）（4分）求证：；

（2）（4分）若点E，F分别为AD，AO的中点，连接EF，，求BD的长及四边形ABCD的周长.

18．（8分）（2022·广元）如图，在四边形ABCD中，ABCD，AC平分∠DAB，AB＝2CD，E为AB中点，连接CE.

（1）（4分）求证：四边形AECD为菱形；

（2）（4分）若∠D＝120°，DC＝2，求△ABC的面积.

19．（8分）（2022·遂宁）如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF.

（1）（4分）求证：△AOE≌△DFE；

（2）（4分）判定四边形AODF的形状并说明理由.

20．（8分）（2022·四川）在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交CE的延长线于点F．

（1）（4分）求证：四边形ADBF是菱形；

（2）（4分）若AB＝8，菱形ADBF的面积为40，求AC的长．

21．（10分）（2022·广州）如图，在菱形ABCD中，∠BAD = 120°，AB = 6，连接BD ．

（1）（4分）求BD的长；

（2）（6分）点E为线段BD上一动点（不与点B，D重合）， 点F在边AD上，且BE=DF，

①当CE丄AB时，求四边形ABEF的面积；

②当四边形ABEF的面积取得最小值时，CE+CF的值是否也最小？如果是，求CE+CF的最小值；如果不是，请说明理由．

22．（10分）（2022·宜昌）已知菱形 中， 是边 的中点， 是边 上一点. 

（1）（6分）如图1，连接 ， . ， . 

①求证： ；

②若 ，求 的长；

（2）（4分）如图2，连接 ， .若 ， ，求 的长. 

23．（10分）（2022·安徽）已知四边形ABCD中，BC＝CD．连接BD，过点C作BD的垂线交AB于点E，连接DE．

（1）（4分）如图1，若，求证：四边形BCDE是菱形；

（2）（6分）如图2，连接AC，设BD，AC相交于点F，DE垂直平分线段AC．

（ⅰ）求∠CED的大小；

（ⅱ）若AF＝AE，求证：BE＝CF．

24．（10分）（2022·安顺）如图1，在矩形中，，，是边上的一点，连接，将矩形沿折叠，顶点恰好落在边上的点处，延长交的延长线于点．

（1）（3分）求线段的长；

（2）（3分）求证四边形为菱形；

（3）（4分）如图2，，分别是线段，上的动点（与端点不重合），且，设，是否存在这样的点，使是直角三角形？若存在，请求出的值；若不存在，请说明理由．

答案解析部分

1．【答案】B

2．【答案】C

3．【答案】A

4．【答案】D

5．【答案】B

6．【答案】D

7．【答案】A

8．【答案】A

9．【答案】C

10．【答案】C

11．【答案】不会

12．【答案】AB=CD或AD∥BC或OA=OC或OB=OD等（只需写出一个条件即可）

13．【答案】64

14．【答案】

15．【答案】

16．【答案】

17．【答案】（1）证明：四边形是平行四边，，

四边形是菱形，

（2）解：点E，F分别为AD，AO的中点，

是的中位线，

，

，

，

四边形是菱形，

，

，

在中，，，

，

菱形形的周长为.

18．【答案】（1）证明：∵ABCD，AC平分∠DAB，

∴∠DAC=∠EAC，∠EAC=∠DCA，

∴∠DAC=∠DCA，

∴DA=DC，

∵AB＝2CD，E为AB中点，

∴，

∵，

∴四边形AECD是平行四边形，

∵DA=DC，

∴四边形AECD是菱形；

（2）解：由（1）知：，

∵∠D＝120°，

∴，

∵E为AB中点，

∴，

∴△BCE是等边三角形，

∴，，

∴，

∴，

∴.

19．【答案】（1）证明：∵E是AD的中点，

∴AE＝DE，

∵DF∥AC，

∴∠OAD＝∠ADF，

∵∠AEO＝∠DEF，

∴△AOE≌△DFE（ASA）.

（2）解：四边形AODF为矩形.

理由：∵△AOE≌△DFE，

∴AO＝DF，

∵DF∥AC，

∴四边形AODF为平行四边形，

∵四边形ABCD为菱形，

∴AC⊥BD，

即∠AOD＝90°，

∴平行四边形AODF为矩形.

20．【答案】（1）证明：∵ ∠BAC＝90°，D是BC的中点，
∴AD=BD=CD，
∵E是AD的中点，即AE=DE，
∵AF∥CD，
∴∠AFE=∠DCE，∠FAE=∠CDE，
∴△AEF≌△DEF(AAS)，
∴AF=CD，
∴AF=BD，
又∵AF∥BD，
∴四边形ADBF是平行四边形，
又AD=BD，
∴ 四边形ADBF是菱形；

（2）解：∵AF∥BC，
∴S△ABD=S△ACD（等底同高），
∵ 四边形ADBF是菱形 ，
∴S△ABD=S△ABF，
∴S△ABC=S△ABD+S△ACD=S△ABD+S△ABF=S菱形ADBF=40，
∵S△ABC=AB×AC=×8×AC=40，

∴AC=10.

21．【答案】（1）解：连接AC，设AC与BD的交点为O，如图，

∵四边形ABCD是菱形，

∴AC⊥BD ， OA=OC，AB∥CD，AC平分∠DAB，

∵∠BAD = 120°，

∴∠CAB=60°，

∴△ABC是等边三角形，

∴BO=AB▪sin60°==，

∴BD=2BO=；

（2）解：如图，过点E作AD的垂线，分别交AD和BC于点M，N，

∵△ABC是等边三角形，

∴AC=AB=6，

由（1）得：BD=；

菱形ABCD中，对角线BD平分∠ABC，AB∥CD，BC=AB=6，

∴MN⊥BC，

∵∠BAD=120°，

∴∠ABC=60°，

∴∠EBN=30°；

∴EN=BE

∵，

∴MN=，

设BE=，则EN=，

∴EM=MN-EN=，

∵S菱形ABCD= AD▪MN=，

∴S△ABD= S菱形ABCD=，

∵BE=DF，

∴DF=，

∴S△DEF=DF ▪EM= =，

记四边形ABEF的面积为s，

∴s= S△ABD - S△DEF =-（），

∵点E在BD上，且不在端点，∴0<BE<BD，即；

①当CE⊥AB时，

∵OB⊥AC，

∴点E是△ABC重心，

∴BE=CE=BO=，

此时 =，

∴当CE⊥AB时，四边形ABEF的面积为；

②作CH⊥AD于H，如图，

∵CO⊥BD，CH⊥AD，而点E和F分别在BD和AD上，

∴当点E和F分别到达点O和点H位置时，CF和CE分别达到最小值；

在菱形ABCD中，AB∥CD，AD=CD，

∵∠BAD=120°，

∴∠ADC=60°，

∴△ACD是等边三角形，

∴AH=DH=3，

∴CH=，

∵，

∴当，即BE=时， s达到最小值，

∵BE=DF，

∴DF=3，

此时点E恰好在点O的位置，而点F也恰好在点H位置，

∴当四边形ABEF面积取得最小值时，CE和CF也恰好同时达到最小值，

∴CE+CF的值达到最小，

其最小值为CO+CH==12．

22．【答案】（1）解：①∵ ， ， 

∴ ，

∵四边形 是菱形，

∴ ， ，

∴ ，

∴ .

②如图，连接 .

∵ 是边 的中点， ，

∴ ，

又由菱形 ，得 ，

∴ 是等边三角形，

∴ ，

在 中， ，

∴ ，

∴ .

（2）解：如图，延长 交 的延长线于点 ， 

由菱形 ，得 ， ，

∴ ， ，

∵ 是边 的中点，

∴ ，

∴ ，

∴ ， ，

∵ ， ，

∴ ， ， ，

∴ ，

∴ ，

∴ ， ，

∴ ，而 为公共角.

∴ ，

∴ ，

又∵ ，

∴ .

23．【答案】（1）证明：

∵DC=BC，CE⊥BD，

∴DO=BO，

∵，

∴，，

∴（AAS），

∴，

∴四边形BCDE为平行四边形，

∵CE⊥BD，

∴四边形BCDE为菱形．

（2）解：（ⅰ）根据解析（1）可知，BO=DO，

∴CE垂直平分BD，

∴BE=DE，

∵BO=DO，

∴∠BEO=∠DEO，

∵DE垂直平分AC，

∴AE=CE，

∵EG⊥AC，

∴∠AEG=∠DEO，

∴∠AEG=∠DEO=∠BEO，

∵∠AEG+∠DEO+∠BEO=180°，

∴．

（ⅱ）连接EF，

∵EG⊥AC，

∴，

∴，

∵

∵AE=AF，

∴，

∴，

，

∴，

∵，

∴，

∴，  

∴，

∴，

，

∴，

，

，

，

∴，

，

∴（AAS），

．

24．【答案】（1）解：如图

四边形 是矩形， ， ，

， ，

将矩形 沿 折叠，顶点 恰好落在 边上的点 处，

，

在 中， ，

，

设 ，则 ，

在 中， ，

，

解得 ，

；

（2）证明： ，

，

四边形 是矩形，

，

，

，

，

，

中， ，

，

，

四边形 为菱形；

（3）解： ，设 ， 是直角三角形

设

由（2）可得

①当 时，如图，

， ，

解得 ；

②当 时，

同理可得

综上所述， 或