2012-2021高考真题分类汇编及详解——不等式选讲

这是一份2012-2021高考真题分类汇编及详解——不等式选讲，文件包含19不等式选讲解析版docx、19不等式选讲原卷版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
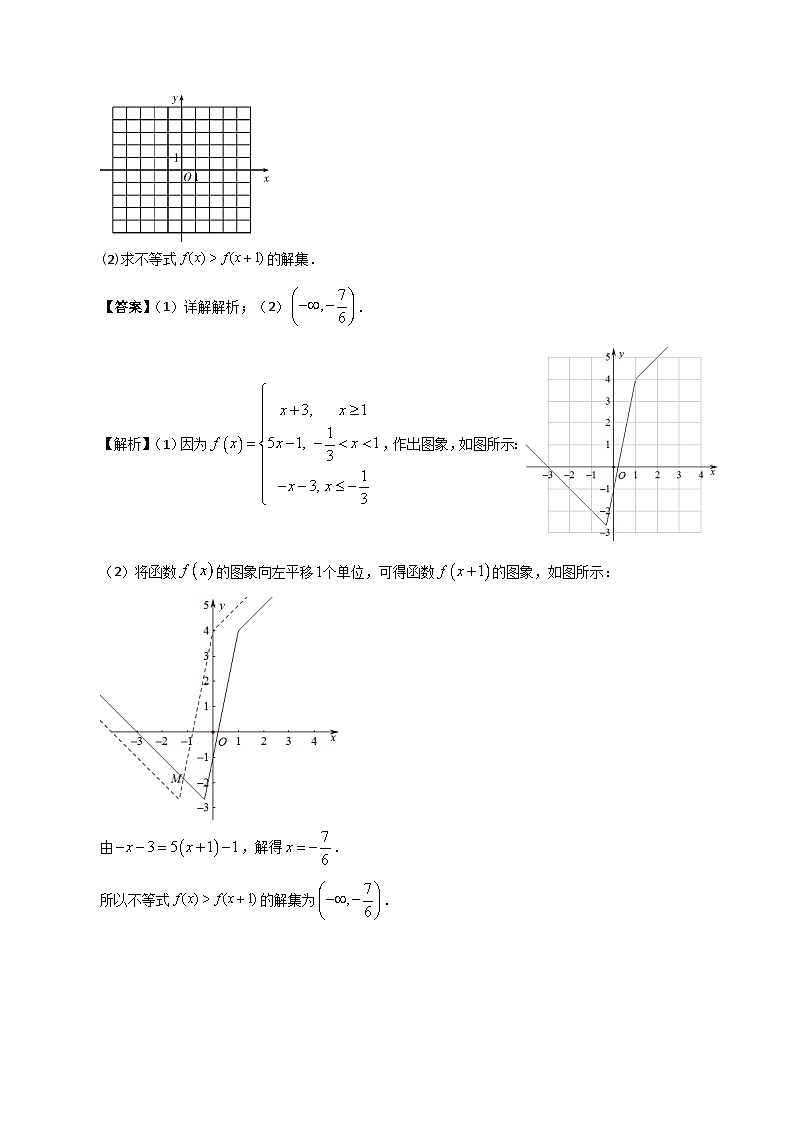
不等式选讲1．(2021年高考全国乙卷理科)已知函数．(1)当时，求不等式的解集;(2)若，求a的取值范围．【答案】（1）．（2）．解析：（1）当时，，表示数轴上的点到和的距离之和，则表示数轴上的点到和的距离之和不小于，故或，所以的解集为．（2）依题意，即恒成立，，故，所以或，解得．所以的取值范围是．【点睛】解绝对值不等式的方法有零点分段法、几何意义法．  2．(2020年高考数学课标Ⅰ卷理科)已知函数．(1)画出的图像；(2)求不等式的解集．【答案】（1）详解解析；（2）．【解析】（1）因为，作出图象，如图所示：（2）将函数的图象向左平移个单位，可得函数的图象，如图所示：由，解得．所以不等式的解集为．  3．(2020年高考数学课标Ⅱ卷理科)已知函数．(1)当时，求不等式的解集；(2)若，求a的取值范围． 【答案】（1）或；（2）．解析：（1）当时，．当时，，解得：；当时，，无解；当时，，解得：；综上所述：的解集为或．（2）（当且仅当时取等号），，解得：或，的取值范围为． 4．(2020年高考数学课标Ⅲ卷理科)设a，b，cR，a+b+c=0，abc=1．(1)证明：ab+bc+ca<0；(2)用max{a，b，c}表示a，b，c中的最大值，证明：max{a，b，c}≥．【答案】（1）证明见解析（2）证明见解析．解析：（1），均不为，则，；（2）不妨设，由可知，，，．当且仅当时，取等号，，即．5．(2019年高考数学课标Ⅲ卷理科)设，且．(1)求的最小值；(2)若成立，证明：或．【答案】【答案】(1)；(2)见详解．【官方解析】（1）由于            故由已知得，当且仅当时等号成立． 所以的最小值为．  （2）由于         故由已知得，当且仅当时等号成立． 因此的最小值为 由题设知，解得或．【解法2】柯西不等式法 (1)，故，当且仅当时等号成立．所以的最小值为．(2)，所以．当且仅当时等号成立．成立．所以成立，所以有或．6．(2019年高考数学课标全国Ⅱ卷理科)已知函数．当时，求不等式的解集；当时，，求的取值范围．【答案】；解析1：”当时，.当时，；当时，.所以，不等式的解集为.因为，所以.当，时，所以，的取值范围是.解析2：当时，原不等式可化为；当时，原不等式可化，即，显然成立，此时解集为；当时，原不等式可化为，解得，此时解集为空集；当时，原不等式可化为，即，显然不成立；此时解集为空集；综上，原不等式的解集为；当时，因为，所以由可得，即，显然恒成立；所以满足题意；当时，，因时， 显然不能成立，所以不满足题意；综上，的取值范围是.  7．(2019年高考数学课标全国Ⅰ卷理科)已知，，为正数，且满足．证明：(1)；(2)．【答案】解：（1）因为，又，故有．所以.（2）因为为正数且，故有所以．8．(2018年高考数学课标Ⅲ卷（理）)【选修4—5：不等式选讲】(10分)设函数．(1)画出的图象；(2)当时，，求的最小值．【答案】【官方解析】（1）的图像如图所示（2）由（1）知，的图像与轴交点的纵坐标为，且各部分所在直线斜率的最大值为，故当且仅当且时，在成立，因此的最小值为．方法2（1），可作出函数的图象如下图（2）依题意可知在上恒成立，在上也恒成立当时，恒成立即在上恒成立所以，且，此时，当时，即恒成立结合，可知即综上可知，所以当，时，取得最小值．9．(2018年高考数学课标Ⅱ卷（理）)[选修4－5：不等式选讲](10分)设函数．(1)当时，求不等式的解集；(2)若，求的取值范围．【答案】解析：（1）当时，可得的解集为．（2）等价于．而，且当时等号成立，故等价于．由可得或，所以的取值范围是．10．(2018年高考数学课标卷Ⅰ（理）)[选修4–5：不等式选讲](10分)已知．(1)当时，求不等式的解集；(2)若时不等式成立，求的取值范围．【答案】解析：（1）当时，，即故不等式的解集为．（2）当时成立等价于当时成立．若，则当时；若，的解集为，所以，故．综上，的取值范围为．11．(2017年高考数学新课标Ⅰ卷理科)[选修4—5:不等式选讲]已知函数,．(1)当时,求不等式的解集;(2)若不等式的解集包含,求的取值范围2017年高考数学新课标Ⅰ卷理科【答案】(1);(2)． 【分析】(1)将代入,不等式等价于,对按,,讨论,得出最值的解集;(2)当时,．若的解集包含,等价于当时,,则在的最小值必为与之一,所以且,得,所以的取值范围为． 【解析】(1)当时,不等式等价于① 当时,①式化为,无解; 当时,①式化为,从而; 当时,①式化为,从而 所以不等式的解集为 (2)当时, 所以的解集包含,等价于当时, 又在的最小值必为与之一,所以,得． 所以的取值范围为． 12．(2017年高考数学课标Ⅲ卷理科)[选修4—5：不等式选讲](10分)已知函数．(1)求不等式的解集；(2)若不等式的解集非空，求的取值范围．解析：（1）因为所以不等式等价于或或由无解；由；由综上可得不等式的解集为．（2）解法一：先求不等式的解集为空集时的取值范围不等式的解集为空集等价于不等式恒成立记，则当时，当时，当时，所以所以不等式的解集为空集时，所以不等式的解集非空时，的取值范围为．解法二：原式等价于存在，使成立，即设由（1）知 当时，，其开口向下，对称轴所以当时，，其开口向下，对称轴为所以当时，，其开口向下，对称轴为所以综上所以的取值范围为．13．(2017年高考数学课标Ⅱ卷理科)[选修4-5：不等式选讲](10分)已知，证明：(1)；(2)．【基本解法】（1）解法一：由柯西不等式得：解法二：解法三：又，所以．当时，等号成立．所以，，即．（2）解法一：由及得所以．解法二：（反证法）假设，则，两边同时立方得：，即，因为，所以，即，矛盾，所以假设不成立，即．解法三：因为，所以：．又，所以: 。所以，，即．14．(2016高考数学课标Ⅲ卷理科)选修4—5:不等式选讲已知函数.(1)当时,求不等式的解集;(2)设函数,当时,,求的取值范围.【解析】(Ⅰ)当时,.解不等式,得.因此,的解集为.(Ⅱ)当时,当时等号成立.所以当时,等价于.①当时,①等价于,无解.当时,①等价于,解得所以的取值范围是.15．(2016高考数学课标Ⅱ卷理科)(本小题满分10分)选修4—5：不等式选讲已知函数，为不等式的解集．（1）求；（2）证明：当时，．方法1（1）当时，由得，解得；当时，恒成立；当时，由，得，解得．所以的解集．（2）由（1）知，当时，，，从而．因此．（方法2）⑴当时，，若；当时，恒成立；当时，，若，．综上可得，．⑵当时，有即， 则，则，即，证毕．16．(2016高考数学课标Ⅰ卷理科)(本小题满分10分)选修4—5：不等式选讲已知函数．（1）画出的图像；（2）求不等式的解集．【答案】    (I)见解析   (II)方法1(I) ，如图所示：(II)由得表达式及图像，当时，得或当时，得或故的解集为；的解集为，解集为．方法2(I) 如上图所示：(II)当，，解得或当，，解得或或当，，解得或  或综上，或或，解集为．17．(2015高考数学新课标2理科)(本小题满分10分)选修4-5不等式选讲设均为正数，且，证明：(1)若，则；(2)是的充要条件．【答案】（Ⅰ）详见解析；（Ⅱ）详见解析．解析：（1）因为，，由题设，，得．因此．（2）（ⅰ）若，则．即．因为，所以，由（Ⅰ）得．（ⅱ）若，则，即．因为，所以，于是．因此，综上，是的充要条件．18．(2015高考数学新课标1理科)(本小题满分10分)选修4—5：不等式选讲已知函数．(1)当时，求不等式的解集；(2)若的图像与轴围成的三角形面积大于6，求的取值范围【答案】（Ⅰ）（Ⅱ）（2，+∞）解析：（Ⅰ）当a=1时，不等式f（x）>1化为|x+1|-2|x-1|＞1，等价于或或，解得，所以不等式f（x）>1的解集为．  （Ⅱ）由题设可得，， 所以函数的图像与轴围成的三角形的三个顶点分别为，，，所以△ABC的面积为．由题设得＞6，解得．所以的取值范围为（2，+∞）．  19．(2014高考数学课标2理科)(本小题满分10)选修4-5：不等式选讲．设函数=(1)证明：2；(2)若，求的取值范围．【答案】解析：（Ⅰ），  仅当时等号成立，所以2．（Ⅱ）=当时，=，解得当时，=，解得综上所述，的取值范围为．20．(2014高考数学课标1理科)选修4—5:不等式选讲若,且． (1)求的最小值;(2)是否存在,使得?并说明理由．【答案】解析:(1)由,得,且当时等号成立, 故,且当时等号成立, ∴的最小值为．                       (2)由,得,又由(1)知,二者矛盾, 所以不存在,使得成立．   21．(2013高考数学新课标2理科)设均为正数，且，证明：(Ⅰ)；(Ⅱ)【答案】证明：(1)由得.由题设得，即.所以，即.(2)因为，故，即.所以.22．(2013高考数学新课标1理科)选修4—5：不等式选讲已知函数=,=．(1)当=2时，求不等式＜的解集；(2)设＞-1,且当∈[，)时，≤,求的取值范围．【答案】（1）　　（2）（-1，]．解析：当=-2时，不等式＜化为，设函数=，=，其图像如图所示，从图像可知，当且仅当时，＜0，∴原不等式解集是． （Ⅱ）当∈[，)时，=，不等式≤化为，∴对∈[，)都成立，故，即≤，∴的取值范围为（-1，]．23．(2012高考数学新课标理科)选修：不等式选讲已知函数．(1)当时，求不等式的解集；(2)若的解集包含，求的取值范围．【答案】（１）{ |≤1或≥8}　　（２）[－3,0]　解析：（1）当时，        或或         或      （2）原命题在上恒成立在上恒成立在上恒成立