2023年北京大兴区初三二模数学试题含答案解析

这是一份2023年北京大兴区初三二模数学试题含答案解析，共14页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
  



                 






  







           
         


                





         












          









     
                            

   





                                


 



          

                                     

 



  
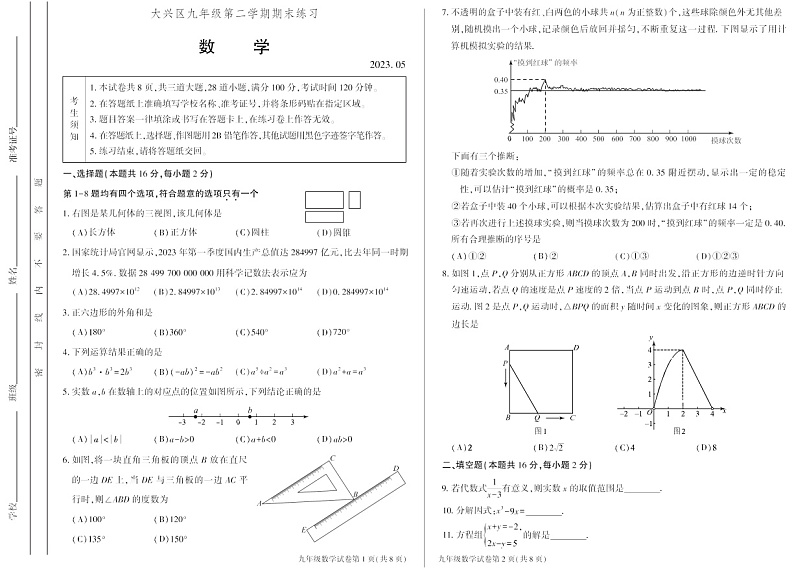
大兴区九年级第二学期二模练习初三数学参考答案及评分标准 一、选择题（本题共 16 分，每小题 2 分） 题号12345678答案ABBCCDAC  二、填空题（本题共 16 分，每小题 2 分）9． x   10． x  x  3 x  3 11． x  1， 12．1 13．B 14．答案不唯一，如 AC=DF，∠A=∠D
15． 103
16．（1）12800；（2）12600
  三、解答题（本题共 68 分，第 17-20 题每小题 5 分，第 21 题 6 分，第 22 题 5 分，第 23-24 题每小题 6 分，第 25 题 5 分，第 26 题 6 分，第 27-28 题，每小题 7 分）
 17．解：原式=2
 2 
2  1  3....................................4 分2
 
=2
 4 ． ……………………………………………………………………….…5
 分2(1  x)＜2  x, ①解：原不等式组为≥ .② 3 2解不等式①，得 x  0 ．.............................................2分解不等式②， 得 x≤3 ．.............................................4分∴ 原不等式组的解集为0  x≤3 ．.....................................5 分解：（1）∵ 函数 y  kx  b(k  0) 的图象平行于函数 y  1 x 的图象，且经过点2, 2 ，     1y       x2
k  1 ，
∴  2
….........................................2 分
2k  b  0.k  1解得 2b  1.∴该函数的表达式为 y  1 x  1 ．..............................3 分2（2） m＞0 ．...................................................5 分  20．（1）补全图形如图所示．           …................................................2 分（2）BC；.....................................................3分一条弧所对的圆周角等于它所对的圆心角的一半．........................5 分  21．（1）∵EF∥AD， ∴∠DAC=∠EFC． ∵∠ACD=∠FCE，CD=CE， ∴△ACD≌△FCE， ∴AD=EF． ∵AD∥EF，AD=EF， ∴四边形 ADFE 是平行四边形．...................................3 分 （2）∵AB=AC，AD⊥BC， ∴BD=CD，
∵CD=2， ∴BD=2． ∵CD=CE， ∴CE=2， ∴DE=4． ∵AE=5， ∴ AD = ， ∴AD=3，AD 3∴sin∠AED= AE = 5 ．∵四边形 ADFE 是平行四边形， ∴AE∥DF， ∴∠EDF=∠AED，3∴sin∠EDF=sin∠AED= 5 ．∵EG⊥DF， ∴∠EGD=90°，EG 3∴sin∠EDF= DE = 5 ．又∵DE=4，12∴ EG= 5 ．.......................................................6分  22．（1）证明：∵   [(m  4)]2  4  4m  m2  8m  16 (m  4)2≥0................................................2 分∴方程总有两个实数根．...........................................3 分（2）解：由求根公式，得x  (m  4)  (m  4)2∴ x1  4 ， x2  m ，...............................................4
分依题意可得 m  1 ．..............................................5 分  解：（1）m=0.10，n=85．.............................................2分（2）七年级，理由如下：因为被抽取的七年级学生成绩的中位数是 81，81<83，所以该生的成绩超过了一半以上被抽取的七年级学生的成绩；因为被抽取的八年级学生成绩的中位数是 85，83<85，所以该生的成绩低于一半被抽取的八年级学生的成绩；所以该名学生是七年级学生．.......................................4 分（3）130．.....................................................6 分  证明：（1）连接 OD． ∵AD 平分∠CAB， ∴∠BAD=∠CAD． ∵OD=OA， ∴∠ODA=∠OAD， ∴∠ODA=∠CAD， ∴OD∥AE， ∴∠E+∠ODE=180°． ∵DE⊥AC． ∴∠E=90°， ∴∠ODE=90°， ∴OD⊥EF． 又∵点 D 在⊙O 上， ∴直线 DE 是⊙O 的切线．.......................................3 分 （2）连接 BC 交 OD 于点 H． ∵AB 为直径， ∴∠ACB=90°， ∴∠BCE=90°． 又∵∠E=90°，∠ODE=90°，
∴四边形 CEDH 为矩形， ∴CH∥EF， ∴∠ABC=∠F，4∴cos∠ABC=cosF= 5 ．BC 4又∵AB=5，cos∠ABC= AB = 5 ，∴BC=4． ∵四边形 CEDH 为矩形， ∴OH⊥BC，1∴CH= 2 BC=2．∵四边形 CEDH 为矩形， ∴DE=CH=2．................................................6 分  解：（1）1；....................................................1 分 由题意可知，抛物线的顶点为（2，1）．则抛物线解析式为 y  a(x  2)2 （1 a  0）．∵ 当 x＝0 时，y＝0， ∴ 0  a(0  2)2  1，解得 a  0.25 ． ∴ 抛物线的解析式为 y  0.25(x  2)2  1 ．..............................3分 （2）<．.......................................................5 分  解：（1）将点（2，1）代入 y  ax2  bx  1a＞0 ，得 4a  2b  1  1b  2a
∴ x   b2a
  2a  1 2a
∴抛物线的对称轴为直线 x  1 ．......................................2分
（2）∵B（3，n） ∴点 B 关于对称轴的对称点坐标为1，n ，∵ a  0 ，∴抛物线开口向上， ∵点 A x0，m，B 3，n 在抛物线上，且 m＜n， ∴ 1＜x0＜3 ， ∵ t≤x0≤t +1 ∴  1＜t 解得1＜t＜2 ．..................................................6 分  27．（1）依题意补全图形，如图 1．..................................1 分

 图 1 图 2 证明：如图 2，过点 A 作 AG⊥BD 于点 G． ∵AC=AD，1∴∠CAG=∠GAD= 2 ∠CAD，∵AG⊥BD， ∴∠ACD+∠CAG=90°． ∵DE⊥AC， ∴∠ACD+∠BDF=90°， ∴∠BDF=∠CAG，1∴∠BDF= 2 ∠CAD．..........................................3 分
（2）如图 2，数量关系：CD= BF． 证明：过点 F 作 FH⊥BC 于点 H． ∵AG⊥BD，∠B=45°， ∴∠BAG=45°． ∵∠FAD=∠BAG+∠GAD， ∴∠FAD=45°+∠GAD． ∵∠AFD=∠B+∠BDF， ∴∠AFD=45°+∠BDF， 又∵∠GAD=∠BDF， ∴∠AFD=∠FAD， ∴DF=AD． ∵FH⊥BC， ∴∠FHD=90°． ∵AG⊥BD， ∴∠AGD=90°， ∴∠FHD=∠AGD． ∵∠BDF=∠GAD， ∴△FHD≌△DGA， ∴FH=GD． 在 Rt△FHB 中，∠B=45°，FH 2∴sinB= BF = 2 ,2∴FH= 2 BF,∵AC=AD，AG⊥CD， ∴CD=2DG， ∴CD=2FH， ∴CD= BF．................................................7 分  
 28．解：（1）① P2
；………………………………………………………………………1
分 ②如图：
 解： ∵r=1， ∴点 A(-1，0），B（1，0）． ∵点 P 为线段 AB 的直点， ∴点 P 在⊙ O 上． 情况 1：连接 CO 交⊙ O 于点 P，此时 CP 最短，连接 CA，∵C（-1，1），A（-1,0）， ∴AC=OA=1，CA⊥AO， ∴ OC = ， ∴ OC = ． ∵CP=CO - OP， ∴ CP =  2-1 ． 情况 2：延长 CO 交⊙ O 于点 P' ，此时CP' 最长． ∵ CP' =CO+ OP' ， ∴ CP' = + 1 ． ∴CP 的取值范围是 2-1≤CP≤ 2+1．....................................5 分 （2）r 的取值范围是 5-1＜r＜6 ．.........................................7分
  解： ∵r=1， ∴点 A(-1，0），B（1，0）． ∵点 P 为线段 AB 的直点， ∴点 P 在以 AB 为直径的⊙ O 上，OP=1．如图，连接 OC，OP．∵C（-1，1），
∴ OC = ． ∴OC>OP ∴ OC-OP≤PC≤OC + OP ∴CP 的取值范围是 2-1≤CP≤ 2+1．