2023年四川省内江市隆昌市第七中学中考三模数学试题(无答案)

隆昌市第七中学2023年中考第三次模拟考试数学试题

出题人：张云刚  审题人：郑兴彬  做题人：周瑜

本试卷分为A卷和B卷两部分．A卷满分100分；B卷满分60分．全卷满分160分，考试时间120分钟．

A卷（共100分）

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的九个选项中，只有一项是符合题目要求的．）

1．如果a与2互为相反数，那么a等于（    ）

A．2  B．  C．  D．

2．2020年是不寻常的一年，据世卫组织统计，截止2020年6月28日全球累计已超过1040万人确诊感染了“新冠”病毒，将数据1040万用科学记数法表示为（    ）

A．  B．  C．  D．

3．如图，一个正方块的六个面分别标有字母A、B、C、D、E、F，从三个方向看到的情况如图所示，则A的对面应该是字母（    ）

A．B  B．C  C．E  D．F

4．若单项式与的和是单项式，则n的值是（    ）

A．3  B．6  C．8  D．9

5．函数中自变量x的取值范围是（    ）

A．  B．且  C．  D．且

6．已知非零实数x满足，则的值为（    ）

A．5  B．7  C．9  D．11

7．按如图所示的程序计算，若开始输入的x的值为，则最后输出的结果是（    ）

A．8  B．64  C．120  D．128

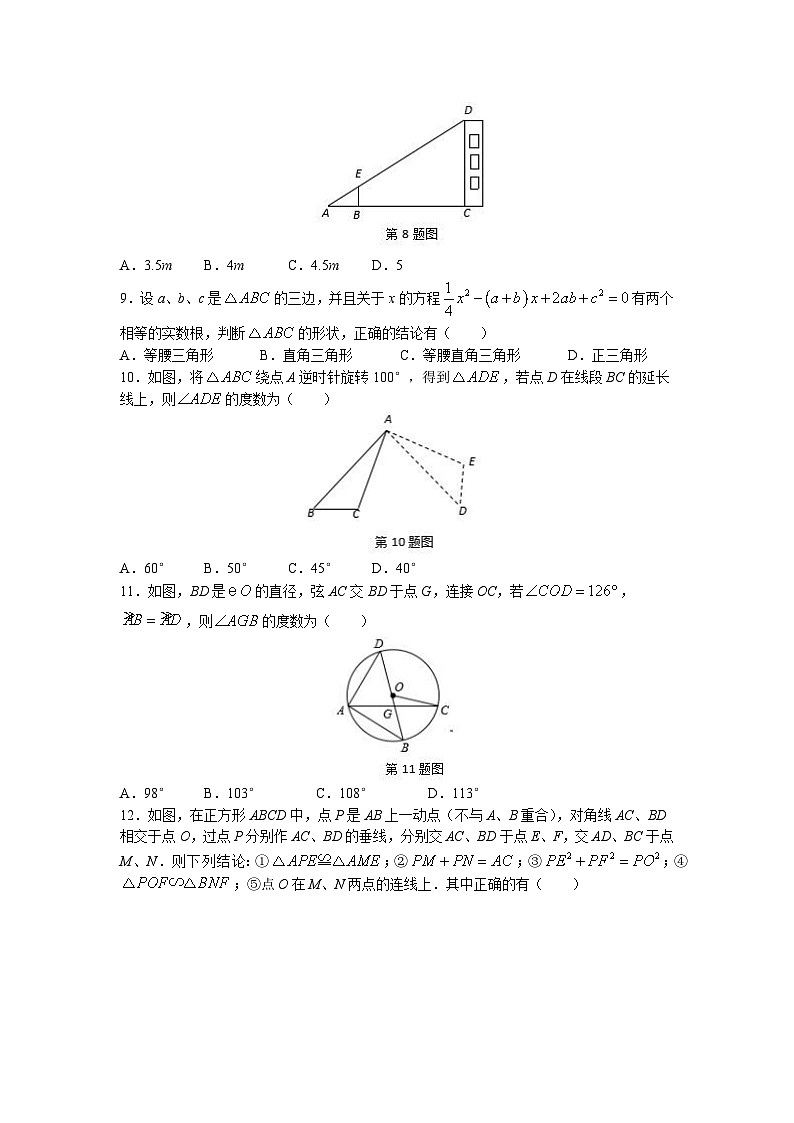
8．如图所示，某校数学兴趣小组利用标杆BE测量建筑物的高度，已知标杆BE高为1.5m，测得，，则建筑物CD的高是（    ）

A．3.5m  B．4m  C．4.5m  D．5

9．设a、b、c是的三边，并且关于x的方程有两个相等的实数根，判断的形状，正确的结论有（    ）

A．等腰三角形  B．直角三角形  C．等腰直角三角形  D．正三角形

10．如图，将绕点A逆时针旋转100°，得到，若点D在线段BC的延长线上，则的度数为（    ）

A．60°  B．50°  C．45°  D．40°

11．如图，BD是的直径，弦AC交BD于点G，连接OC，若，，则的度数为（    ）

A．98°  B．103°  C．108°  D．113°

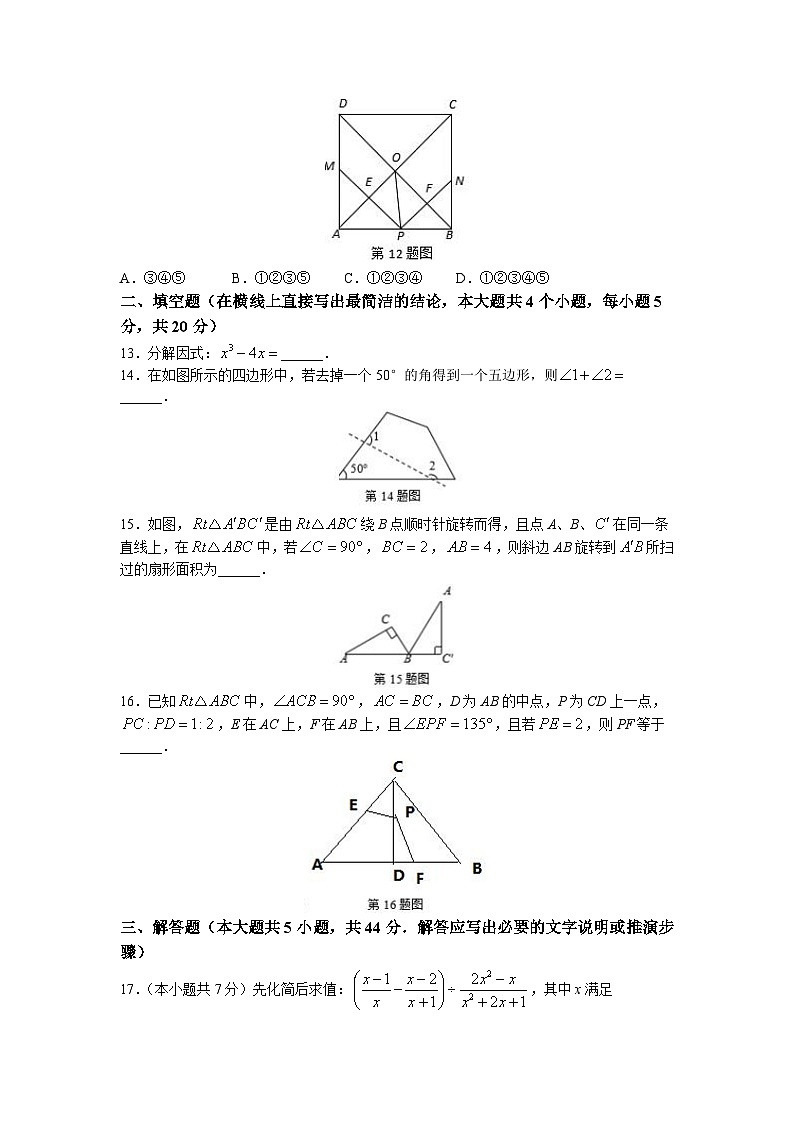
12．如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N．则下列结论：①；②；③；④；⑤点O在M、N两点的连线上．其中正确的有（    ）

A．③④⑤  B．①②③⑤  C．①②③④  D．①②③④⑤

二、填空题（在横线上直接写出最简洁的结论，本大题共4个小题，每小题5分，共20分）

13．分解因式：______．

14．在如图所示的四边形中，若去掉一个50°的角得到一个五边形，则______．

15．如图，是由绕B点顺时针旋转而得，且点A、B、在同一条直线上，在中，若，，，则斜边AB旋转到所扫过的扇形面积为______．

16．已知中，，，D为AB的中点，P为CD上一点，，E在AC上，F在AB上，且，且若，则PF等于______．

三、解答题（本大题共5小题，共44分．解答应写出必要的文字说明或推演步骤）

17．（本小题共7分）先化简后求值：，其中x满足

18．（本小题满分9分）如图，在□ABCD中，对角线AC，BD交于点O，点E、点F在BD上，且，连接AE并延长，交BC于点G，连接CF并延长，交AD于点H．

（1）求证：；【4分】

（2）若AC平分，求证：四边形AGCH是菱形．【5分】

19．（本小题满分9分）为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球；B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图1、图2的统计图．请结合图中的信息解答下列问题：

（1）在这项调查中，共调查了多少名学生？【2分】

（2）请计算本项调查中喜欢“立定跳远”的学生人数______和所占百分比______，并将两个统计图补充完整；【3分】

（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．【4分】

20．（本小题满分9分）第十一届全国少数民族传统体育运动会于2019年9月8日在郑州举行，其中，花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行．如图，钟楼是郑州大学主校区标志性建筑物之一，小刚站在钟楼前C处测得钟楼顶A的仰角为53°，小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°，两人的水平距离EC为4m，已知教学楼三楼所在的高度为10m，根据测量数据，计算钟楼AB的高度（结果精确到1米，参考数据：，，）

21．（本小题满分10分）一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：

已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行．受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完．

（1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？【4分】

（2）如果先进行精加工，然后进行粗加工．

①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；【3分】

②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？【3分】

B卷（共60分）

四、填空题（本大题共4小题，每小题6分，共24分．）

22．已知，那么的值为______．

23．已知，n是关于x的一元二次方程的两个不相等的实数根，且，则q的取值范围是______．

24．如图，以的边AB、AC为边向外作正方形ABEF和正方形ACGD，连接BD、CF、DF，若，，则的值______．

25．对于实数，规定，例如，，那么计算的结果是______．

二、解答题（本大题共3个小题，每小题12分，共36分、解答题必须写出必要的文字说明、证明过程或推演步骤）

26．如图，在中，，点E在斜边AB上，以AE为直径的与BC相切于点D．

（1）求证：AD平分；【4分】

（2）若，．①求AD的值；【4分】②求图中阴影部分的面积．【4分】

27．（本小题满分12分）阅读下列材料：我们知道的几何意义是在数轴上数x对应的点与原点的距离；即；这个结论可以推广为表示数轴上数，对应点之间的距离．绝对值的几何意义在解题中有着广泛地应用．

例1：解方程

容易得出，在数轴上与原点距离为4的点对应的数为，即该方程的解为

例2：解方程

由绝对值的几何意义可知，该方程表示求数轴上与和2的距离之和为5的点对应的x的值，在数轴上，和2的距离为3，满足方程的x对应的点在2的右边或在的左边．若x对应的点在2的右边，如图1可以看出；同理，若x对应的点在的左边，可得，所以原方程的解是或

例3：解不等式

在数轴上找出的解，即到1的距离为3的点对应的数为，4，如图2，在的左边或在4的右边的x的值就满足，所以的解为或

参考阅读材料，解得下列问题：

（1）方程的解为______；【4分】

（2）方程的解为______；【请仿图1画出解题过程4分】

（3）若，求x的取值范围．【请写出必要的过程4分】

28．（本小题满分12分）如图，抛物线交x轴于，两点，与y轴交于点C，连接AC、BC．点P是第一象限内抛物线上的一动点，点P的横坐标为m．

（1）求此抛物线的表达式；【4分】

（2）过点P作，垂足为点N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？【4分】

（3）过点P作轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由．【4分】