2023年重庆市第一中学校中考一模数学试题（解析版）

这是一份2023年重庆市第一中学校中考一模数学试题（解析版），共44页。试卷主要包含了 9的相反数是， 估计的值应为等内容，欢迎下载使用。

重庆一中初2023届22-23学年下期阶段性消化作业（三）
数学试题2023.5
（全卷共四个大题，满分150分，考试时间120分钟）
注意事项：
1．试题的答案书写在答题卷上，不得在试卷上直接作答；
2．作答前认真阅读答题卷上的注意事项；
3．作图（包括作辅助线）请一律用2B铅笔完成；
4．考试结束，由监考人员将试题和答题卷一并收回．
参考公式：抛物线的顶点坐标为，对称轴为直线．
一、选择题：（本大题共10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．
1. 9的相反数是（ ）
A. B. C. 9 D.
【答案】D
【解析】
【分析】根据相反数的概念：只有符号不同的两个数叫做互为相反数可得答案．
【详解】解：9的相反数是，
故选：．
【点睛】本题主要考查了相反数，解题的关键是掌握相反数（只有符号不同的两个数叫做互为相反数）的概念．
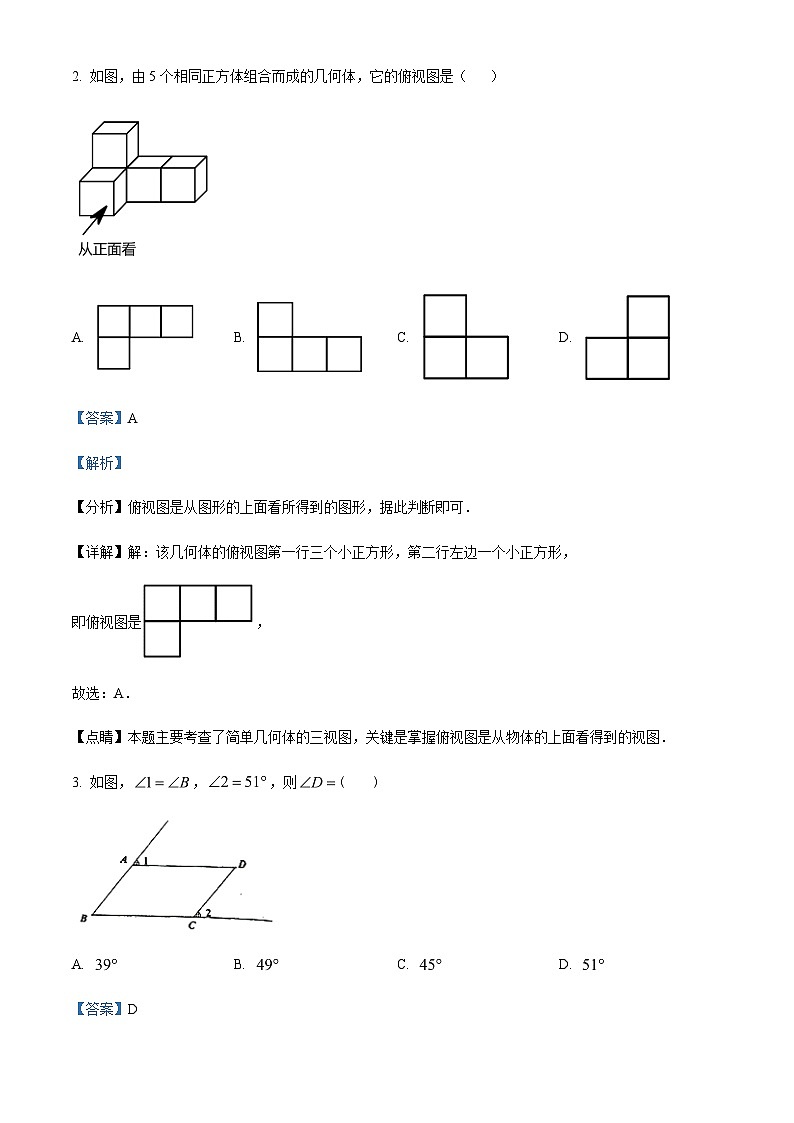
2. 如图，由5个相同正方体组合而成的几何体，它的俯视图是（ ）

A. B. C. D.
【答案】A
【解析】
【分析】俯视图是从图形的上面看所得到的图形，据此判断即可．
【详解】解：该几何体的俯视图第一行三个小正方形，第二行左边一个小正方形，
即俯视图是，
故选：A．
【点睛】本题主要考查了简单几何体的三视图，关键是掌握俯视图是从物体的上面看得到的视图．
3. 如图，，，则(　　)

A. B. C. D.
【答案】D
【解析】
【分析】根据，得出，进而根据两直线平行内错角相等即可求解．
【详解】解：∵，
∴
又∵，
∴，
故选：D．
【点睛】本题考查了平行线的性质与判定，熟练掌握平行线的性质与判定是解题的关键．
4. 反比例函数的图象过，则k的值为（　　）
A. 15 B. 18 C. 21 D. 25
【答案】C
【解析】
【分析】根据反比例函数的图象过，可得，即可求解．
【详解】解：∵反比例函数的图象过，
∴，
解得：．
故选：C．
【点睛】本题考查了反比例函数图象上点的坐标特征，比较简单，考查的是用待定系数法求反比例函数的比例系数，是中学阶段的重点．
5. 如图，和是位似图形，点是位似中心，若，的面积为，则的面积为（　　）

A. 1 B. C. D.
【答案】D
【解析】
【分析】先求出位似比，再直接利用面积比等于位似比的平方即可得出答案．
【详解】解：∵和是位似图形，点O为位似中心，，，
∴，
∵的面积为9，
∴的面积为．
故选：D．
【点睛】此题主要考查了位似变换，掌握相似三角形的性质是解题关键．
6. 如图，每个图形都由同样大小的“△”按照一定的规律组成，其中第1个图形有5个“△”，第2个图形有10个“△”，第3个图形有15个“△”，…，则第8个图形中“△”的个数为（　　）

A. 40 B. 42 C. 44 D. 46
【答案】A
【解析】
【分析】观察图形，找到图形变化的规律，利用规律求解即可．
【详解】解：根据题意可得：
图中有个△，
图中有个△，
图中有个△，
图中有个△，
…，
则第8个图形中有个△，
故选：A．
【点睛】本题是对图形变化规律的考查，解题的关键是仔细观察图形并找到图形的变化规律，难度不大．
7. 估计的值应为（　　）
A. 4和5之间 B. 5和6之间 C. 6和7之间 D. 7和8之间
【答案】C
【解析】
【分析】直接利用二次根式乘法运算法则化简，进而估算无理数大小即可．
【详解】解：，
∵，
∴，
故选：C．
【点睛】此题主要考查了估算无理数的大小，正确进行二次根式的运算是解题的关键．
8. 如图，在矩形中，E、F为上一点，，，连接、，若，则的度数为（　　）

A. B. C. D.
【答案】B
【解析】
【分析】先证明，即可得出，再根据矩形的性质得出，最后根据等边对等角即可求解．
【详解】解：∵，
∴，即，
∵四边形为矩形，
∴，，
∴，
∵，
∴，
∴，
∴，
故选：B．
【点睛】本题主要考查了矩形的性质，和等腰三角形的性质，解题的关键是掌握矩形对边平行且相等，等腰三角形“等边对等角”．
9. 如图，是的直径，为上一点，连接，于点，是的切线，且，若，，则的长为（　　）

A. B. 4 C. D.
【答案】D
【解析】
【分析】连接，根据题意可得，，从而可得，由为的中点可得为的中位线，从而可得，由勾股定理可得，最后由得到，即可得到答案．
【详解】解：如图所示，连接，
，
根据题意可得：，，
，
，
为的中点，
为的中点，
为的中位线，
，
，
，
，
，
，即，
，
故选：D．
【点睛】本题主要考查了圆周角定理，勾股定理，三角形相似的判定与性质，熟练掌握圆周角定理，三角形相似的判定与性质，添加适当的辅助线是解题的关键．
10. 在多项式中，除首尾项a、外，其余各项都可闪退，闪退项的前面部分和其后面部分都加上绝对值，并用减号连接，则称此为“闪减操作”．每种“闪减操作”可以闪退的项数分别为一项，两项，三项．“闪减操作”只针对多项式进行．例如：“闪减操作”为，与同时“闪减操作”为，…，下列说法：
①存在对两种不同的“闪减操作”后的式子作差，结果不含与e相关的项；
②若每种操作只闪退一项，则对三种不同“闪减操作”的结果进行去绝对值，共有8种不同的结果；
③若可以闪退的三项，，满足：
，则的最小值为．
其中正确的个数是（　　）
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】
【分析】①根据“闪减操作”的定义，举出符合条件的式子进行验证即可；
②先根据“闪减操作”的定义进行运算，再分类讨论去绝对值，即可判断；
③根据“闪减操作”的定义和绝对值的几何意义，求出，，的最小值，即可得出结论．
【详解】①“闪减操作”后的式子为，“闪减操作”后的式子为，对这两个式子作差，得：
，
结果不含与e相关的项，故①正确；
②若每种操作只闪退一项，共有三种不同“闪减操作”：
“闪减操作”结果为，
当时，，
当时，，
当时，，
当时，，
“闪减操作”结果为，
当时，，
当时，，
当时，，
当时，，
“闪减操作”结果为，
当时，，
当时，，
当时，，
当时，，
共有12种不同的结果，故②错误；
③∵，在数轴上表示点与和的距离之和，
∴当距离取最小值时，的最小值为，
同理：，在数轴上表示点与和的距离之和，
∴当距离取最小值时，的最小值为，
，在数轴上表示点与和的距离之和，
∴当距离取最小值时，的最小值为，
∴当，，都取最小值时，
，
此时，的最小值为，故③正确；
故选C．
【点睛】本题主要考查了新定义运算，绝对值的几何意义，熟练掌握绝对值的性质是解题的关键．
二、填空题（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上．
11. 计算：___________．
【答案】##
【解析】
【分析】先分别化简负整数指数幂和绝对值，然后再计算．
【详解】解：，
故答案为：．
【点睛】本题考查负整数指数幂及实数混合运算，掌握运算法则准确计算是解题关键．
12. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是______．
【答案】8
【解析】
【分析】根据多边形的内角和定理，多边形的内角和等于（n﹣2）•180°，外角和等于360°，然后列方程求解即可．
【详解】解：设边数为n，由题意得，
180（n－2）=3603，
解得n=8．
所以这个多边形的边数是8．
故答案为：8．
【点睛】本题主要考查了多边形的内角和公式与外角和定理，根据题意列出方程是解题的关键．
13. 已知一个不透明的盒子里装有4个球，其中1个红球，3个白球，这些球除颜色外其它均相同，现从中随机地摸出一个小球，不放回，然后再从剩下的小球中随机摸出一个，则摸出的两个小球恰好都是白球的概率为___________．
【答案】
【解析】
【分析】根据题意，列出表格，数出所求的情况数和符合条件的情况数，再用概率公式求解．
【详解】解：列出表格如下：

红
白1
白2
白3
红

（红，白1）
（红，白2）
（红，白3）
白1
（白1，红）

（白1，白2）
（白1，白3）
白2
（白2，红）
（白2，白1）

（白2，白3）
白3
（白3，红）
（白3，白1）
（白3，白2）

一共有12中情况，摸出的两个小球恰好都是白球的6中，
∴摸出的两个小球恰好都是白球的概率．
故答案为：．
【点睛】本题考查了列表法或树状图法求概率，列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适用于两步或两步以上完成的事件；解题时还要注意是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
14. 一个等腰三角形的顶角为140°，则它一腰上的高与另一腰的夹角为___________．
【答案】
【解析】
【分析】根据题意画出图形，先求出，再根据直角三角形的两锐角互余即可求解．
【详解】解：如图所示，

∵，
∴
∵是上的高，
∴
∴
故答案为：．
【点睛】本题考查了等腰三角形的性质，三角形内角和定理，直角三角形的两锐角互余，熟练掌握等腰三角形的性质是解题的关键．
15. 某口罩厂一月份口罩产量为160万只，由于市场需求逐渐减少，三月份的产量减少到90万只．假设该厂二、三月份的口罩产量的月平均减少率为，则可列方程为___________．
【答案】
【解析】
【分析】根据题意和题目中的数据，可以得到方程，即可解决本题．
【详解】解：根据题意可得：
，
故答案为：．
【点睛】本题主要考查了由实际问题抽象出一元二次方程，解答本题的关键是明确题意，列出相应的方程．
16. 如图，在菱形中，，对角线，交于点O．以为直径在上方作半圆，半圆与交于点E，再以B为圆心，为半径作弧．若，则图中阴影部分的面积为___________．（结果保留）

【答案】
【解析】
【分析】连接点E和中点F，交于点G，易证为等边三角形，求出，再证明为等边三角形，即可求出和，最后根据阴影部分的面积即可求解．
【详解】解：连接点E和中点F，交于点G，
∵四边形为菱形，，
∴，，，
∵，
∴为等边三角形，，
在中，，
∴，
∵，
∴为等边三角形，则，
∵点F为中点，
∴，
∴，
∵，
∴为中位线，则，
∵，
∴，
∴，
∴，
∴阴影部分的面积，
故答案为：．

【点睛】本题主要考查了求不规则则图形的面积，解题的关键是掌握求扇形面积的方法和步骤，得出阴影部分的面积．
17. 若关于x的不等式组有且只有四个整数解，且关于y的分式方程的解为非正数，则符合条件的所有整数a的和为___________．
【答案】
【解析】
【分析】先求出不等式组和分式方程的解，再根据解的情况确定a的范围，即可求解．
【详解】解不等式，得，
解不等式，得，
∴不等式组的解集为，
∵不等式组有且只有四个整数解，
∴，即，
解得，
∵解为非正数，
∴且，即且，
∴符合条件的整数a有，
∴符合条件的所有整数a的和为，
故答案为：．
【点睛】本题考查了解不等式组和解分式方程，根据不等式组的解的情况和分式方程的解的情况确定出a的范围是解题的关键．
18. 一个四位正整数，其中，，，，且，，，均为整数．的千位数字与十位数字之和等于百位数字与个位数字之和，将的千位数字和百位数字组成的两位数记为，十位数字和个位数字组成的两位数记为．记的千位数字与个位数字的乘积为，百位数字与十位数字的乘积为．若被7除余4，则___________，在此条件下，当（为整数）时，最大的四位正整数___________．
【答案】 ①. 6 ②. 8316
【解析】
【分析】（1）根据题意，找出千位数字，百位数字b，十位数字，个位数字，再根据条件列数相关算式，即可解决问题
（2）先通过算式分别表示和，在通过条件化简整式，利用条件找出符合题意的最大的A
【详解】解：（1）由题干可得：千位数字，百位数字b，十位数字，个位数字

可得：
∵，且为整数
∴
（2）


由可得：

∴
等号左边是9的倍数，∴
个位越大，A越大，所以A最大＝8316
【点睛】本题属于数与式中的新定义问题，理解题意，正确掌握整式的化简是解题关键
三、解答题（本大题共2个小题，19题8分，20题10分，共18分），解题时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括作辅助线），请将解答过程书写在答题卡中对应的位置上．
19. 如图，四边形为矩形，为矩形的一条对角线．

（1）用尺规完成以下基本作图：在的左侧作，射线与的延长线交于点E．连接与交于点F；（保留作图痕迹，不写做法，不下结论）
（2）小亮判断点F为线段的中点．他的证明思路是：利用矩形的性质，先证明为等腰三角形，从而得到点B为的中点，再利用三角形全等，得到点F为的中点．请根据小亮的思路完成下面的填空：
证明：∵四边形为矩形
∴，，，
∵，
∴①___________，
∵，
∴，
∵，
∴，
∴，，
∴②___________，
∴，
∵，
∴，
∴③___________，
∵，
∴，
∵，，
∴④___________，
∴，
∴点F为的中点．
【答案】（1）见解析 （2）①，②，③，④
【解析】
【分析】（1）过点A作，交的延长线交于点E．连接与交于点F；
（2）利用矩形的性质，先证明为等腰三角形，从而得到点B为的中点，再利用，得到点F为的中点．
【小问1详解】
解：如图所示，点E和点F即为所求，
【小问2详解】
证明：∵四边形为矩形
∴，，，
∵，
∴，
∵，
∴，
∵，
∴，
∴，，
∴，
∴，
∵，
∴，
∴③，
∵，
∴，
∵，，
∴④，
∴，
∴点F为的中点．
故答案为：，，，．
【点睛】本题主要考查了尺规作图，矩形的性质，等腰三角形的性质，全等三角形的判定和性质，解题的关键是按照题目要求作图，熟练掌握相关知识点并灵活运用．
20. 计算：
（1）
（2）
【答案】（1）
（2）
【解析】
【分析】（1）根据完全平方公式，单项式乘以多项式进行计算即可求解；
（2）根据分式的混合运算进行化简即可求解．
【小问1详解】
解：


；
【小问2详解】
解：


．
【点睛】本题考查了整式的乘法以及分式的混合运算，熟练掌握整式的乘法运算以及分式的运算法则是解题的关键．
四、解答题（本大题共6个小题，每题10分，共60分），解题时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括作辅助线），请将解答过程书写在答题卡中对应的位置上．
21. 某校为了解学生对共青团的认识，组织七、八年级全体学生进行了“团史知识”竞赛，为了解竞赛成绩，现从该校七、八年级中各随机抽取10名学生的竞赛成绩（满分100分，90分及90分以上为优秀）进行整理、描述和分析（成绩得分用x表示，共分成四组：，，，，下面给出了部分信息：
七年级抽取的名学生的竞赛成绩是：，，，，，，，，，
八年级抽取的名学生的竞赛成绩在组中的数据是：，，
七、八年级抽取的学生竞赛成绩统计表：
年级
平均数
中位数
众数
方差
七年级




八年级





根据以上信息，解答下列问题：
（1）图表中___________，___________，___________；
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握团史知识较好？请说明理由（一条理由即可）；
（3）该校七年级有人，八年级有人参加了此次“团史知识”竞赛，估计参加竞赛活动成绩优秀的学生人数是多少？
【答案】（1）
（2）八年级的学生掌握团史知识较好，理由见解析
（3）
【解析】
【分析】（1）根据扇形图信息可求八年级的人数，可确定的值，根据七年级的分数和确定众数的方法可确定的值；
（2）根据众数的情况可得答案（说明理由不唯一）；
（3）根据样本百分比估算总体情况即可求解．
【小问1详解】
解：七、八年级中各随机抽取名学生，
∴八年级组的人数是：（名），组的人数是：（名），组的人数是：（名），组的人数是：（名），
∴八年级中有名，有名，有名，有名，
∴组的百分比为，中位数在组中且组中的数据是：
∴中位数是和的一半，即，
观察七年级的成绩，众数是，
∴，
故答案为：．
【小问2详解】
解：七年级的众数是，八年级的众数是，说明八年级的学生掌握团史知识较好．
【小问3详解】
解：七年级中优秀的学生人数名，八年级中优秀的学生人数名，
该校七年级有人，八年级有人参加了此次“团史知识”竞赛，
估计参加竞赛活动成绩优秀的学生人数是（名）．
【点睛】本题主要考查调查统计的相关知识，掌握中位数，众数，样本百分比的计算方法，根据样本估算总体的方法是解题的关键．
22. 某工厂正在生产某种仪器的部件．
（1）一套仪器由一个A部件和三个B部件构成．用钢材可做60个A部件或300个B部件．现将（钢材全部用于制作这种仪器，应用多少钢材做A部件，才能使生产的A，B部件恰好配套？
（2）甲、乙两个车间接到任务生产一批A部件．若甲车间单独完成，则恰好能在规定工期完成，若乙车间单独完成，则需要比规定工期多用6天．若甲、乙两车间合作4天，剩下的由乙车间单独完成，也正好按照规定工期完成，则生产这批A部件的规定工期为多少天？
【答案】（1）用钢材做A部件
（2）12天
【解析】
【分析】（1）设用钢材做A部件，根据“生产的A，B部件恰好配套”列出方程，解之即可；
（2）设规定的工期为天，根据“若甲、乙两车间合作4天，剩下的由乙车间单独完成，也正好按照规定工期完成”列出方程，解之即可．
【小问1详解】
解：设用钢材做A部件，
由题意可得：，
解得：，
，
∴应用钢材做A部件，钢材做B部件，才能使生产的A，B部件恰好配套．
【小问2详解】
设规定的工期为天，
由题意可得：，
解得：，
经检验：是原方程的解，

∴规定的工期为12天．
【点睛】本题考查了一元一次方程的应用，分式方程的应用，找准等量关系，正确列出相应方程是解题关键．
23. 如图，正方形的边长为，交于点O，一动点M从D点出发，沿以每秒2个单位的速度运动到点A时停止，设运动时间为t秒，．

（1）直接写出y与t的函数关系式，并注明t的取值范围，并在下面的平面直角坐标系中直接画出y的函数图象；
（2）根据所画的y与t的函数图象，写出该函数的一条性质；___________；
（3）已知函数的图象如图所示，结合你所画的函数图象，直接估计当时t的取值范围：___________．（结果保留1位小数，误差不超过）
【答案】（1），函数图象见解析
（2）该函数的最大值为8（答案不唯一）
（3）或
【解析】
【分析】（1）先根据正方形的性质求出，再分两种情况，如图1-1所示，当点M在上，即时，过点M作于N，则是等腰直角三角形，如图2-2所示，当点M在上，即时，过点M作于N，则是等腰直角三角形，两种情况求出的长，再根据三角形面积公式求出对应的函数关系式，最后在坐标系中画出对应的函数图象即可；
（2）根据（1）所画函数图象，写出其一条性质即可；
（3）先求出两函数的交点横坐标，然后根据图象法求解即可．
【小问1详解】
解：∵四边形是正方形，
∴，，
∵正方形的边长为，即，
∴；
如图1-1所示，当点M在上，即时，过点M作于N，则是等腰直角三角形，
∴，
∴；

如图2-2所示，当点M在上，即时，过点M作于N，则是等腰直角三角形，
∴，
∴；
综上所述，；

函数图象如图1-3所示，
【小问2详解】
解：由函数图象可知，该函数的最大值为8；
故答案为：该函数的最大值为8（答案不唯一）；
【小问3详解】
解：联立，解得或（舍去）
联立解得（舍去）或，
∴反比例函数与函数的两个交点的横坐标分别为，，
∴由函数图象可知当或时，，
故答案为：或．

【点睛】本题主要考查了一次函数与反比例函数综合，画一次函数图象，正方形的性质，勾股定理，等腰直角三角形的性质等等，利用数形结合和分类讨论的思想求解是解题的关键．
24. 如图，一条自西向东的道路上有两个公交站点，分别是和，在的北偏东方向上有另一公交站点．经测量，在的北偏西方向上，一辆公交车从出发，沿行驶米到达处，此时在的西南方向．（参考数据：，）

（1）求的距离；（结果保留根号）
（2）该公交车原计划由行驶，其平均速度为米分，但当行驶到点时，接到通知，段道路正在维修，需要沿绕道行驶，为了尽快到达站点，绕道时其平均速度提升到米分．那么原计划所用时间和实际所用时间相比，哪个更少？请说明理由．（结果保留位小数）
【答案】（1）（米）
（2）原计划所用时间较少，理由见解析
【解析】
【分析】（1）过点，作于点，根据题意可得，求得，进而得出，进而得出的长；
（2）根据题意，求得，然后根据路程除以速度，比较两段时间，即可求解．
【小问1详解】
解：如图所示，过点，作于点，

根据题意可得，
在中，，
在中，，
在中，，
∵，
，
∴，
∴（米），
【小问2详解】
解：，
，
行驶所需时间为：分，
沿绕道行驶所需时间为：分，
∵，
∴原计划所用时间较少．
【点睛】本题考查了解直角三角形的应用，方位角问题，构造直角三角形是解题的关键．
25. 如图，抛物线与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，抛物线的对称轴与直线的交点为E．

（1）如图1，求直线的表达式；
（2）如图1，点P是直线上方抛物线上的一动点，过点P作y轴的平行线交直线于点Q，过点P作x轴的平行线交直线于点H，求周长的最大值和此时P点的坐标；
（3）如图2，将抛物线沿射线方向平移4个单位得到新抛物线，新抛物线与坐标轴y轴交于点M．点D与点C关于x轴对称，连接，将沿直线平移得到．平移过程中，在直线上是否存在点N，使得N，，，为顶点的四边形是菱形，若存在，请直接写出N点的坐标，并写出求解其中一个N点坐标的过程．
【答案】（1）
（2），
（3）
【解析】
【分析】（1）根据抛物线解析式，确定A、B、C的坐标，再利用待定系数法确定解析式即可．
（2）根据，得到，继而得到，得到周长等于，设点，则，确定，根据二次函数最值计算即可．
（3）根据抛物线沿射线方向平移4个单位得到新抛物线，结合，得到即将，为向左平移个单位长，再向上平移2个单位长，得到，整理得到如下解析式：
确定M的坐标，从而确定直线的解析式， 根据得到，设平移变换为向右平移个单位长，再向上平移个单位长，根据确定，根据菱形的对角线互相垂直平分，得到N的坐标，代入直线的解析式确定t即可．
小问1详解】
∵，抛物线与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，
令，
∴，
解得；
令，
∴，
∴，
设的解析式为，
∴，
解得，
故直线的解析式为．
【小问2详解】
∵，
∴，
∴，
∴，
∵轴，轴，
∴，
∴，
∴周长等于，
∵，
设点，则，
∴，

故当时，取得最大值，且最大值为，
此时，，
故周长的最大值为，此时P点的坐标是．
【小问3详解】
∵抛物线沿射线方向平移4个单位得到新抛物线，，∴即将，为向左平移个单位长，再向上平移2个单位长，得到，
整理得，
∴M的坐标为，
∵直线的解析式为，抛物线的顶点坐标为，
∴，
设的解析式为，
∴，
解得，
故直线的解析式为．
∵，

∴，设平移变换为向右平移个单位长，再向上平移个单位长，
∵，
∴，
∵菱形的对角线互相垂直平分，轴，，
∴轴，
∴对角线交点坐标为，，
∴，
解得，
∴，
∴，
解得，
∴．
【点睛】本题考查了抛物线与一元二次方程，三角函数的应用，构造二次函数求最值，平移规律，一次函数解析式的确定，菱形的性质，中点坐标公式，熟练掌握三角函数的应用，构造二次函数求最值，平移规律，菱形的性质，中点坐标公式．
26. 如图，在中，，点E为边上一点，连接．

（1）如图1，若，，，求线段BE的长；
（2）如图2，若 ，G为边上一点且，F为上一点且，H为的中点，连接，，，．猜想与之间存在的数量关系，并证明你的猜想；
（3）如图3，当，时，将绕着点E沿顺时针方向旋转90°得到，连接．点P、点Q分别是线段、上的两个动点，连接、．点H为延长线上一点，连接，将沿直线翻折到同一平面内的，连接．在P、Q运动过程中，当取得最小值且，时，请直接写出四边形的面积．
【答案】（1）6 （2）
（3）
【解析】
【分析】（1）如图，过作于，过作于，证明四边形是矩形，，而，可得，而，再利用勾股定理可得答案；
（2）如图，取中点，连接，，证明为等边三角形，可得，证明，，，，，再证明，．
（3）如图，由旋转的性质可得：，，证明关于的对称点在上，可得当三点共线，且时，此时最小，此时，证明三点共线，求解，可得，证明，可得，如图，作，则，设，，可得，解得：，利用可得答案．
【小问1详解】
解：如图，过作于，过作于，

∵，，
∴四边形是矩形，，而，
∴，而，
∴，
∴；
【小问2详解】
如图，取的中点，连接，，
∵，，
∴为等边三角形，
∴，

∵，
∴，，，
∵，
∴，
∴，
∴，，
∵为的中位线，
∴，，，
∴，，
∴，
∴，而，
∴，
∴，
∴．
【小问3详解】
如图，由旋转的性质可得：，，
∴，
∵，则，
∴关于的对称点在上，
当三点共线，且时，最小，
此时，
∴，
∵，，
∴，

∴，，
∴，
∵，结合对称可得：，
∴，
∴三点共线，
∵，
∴，
∴，
由，
∴，
∴，
∴，
如图，作，则，

∴设，，
∴，
解得：，
∴




．
【点睛】本题考查的是矩形的判定与性质，等腰直角三角形的判定与性质，勾股定理的应用，等边三角形的判定与性质，相似三角形的判定与性质，轴对称的性质，锐角三角函数的应用，本题难度大，综合程度高，计算量大，典型的中考压轴题．