
2023年广东省深圳市宝安区中考数学+仿真+模拟试卷(含答案)
展开2023年广东省深圳市宝安区中考数学 仿真 模拟试卷
一、选择题(本大题共10小题,共30.0分)
1. 的算术平方根是( )
A. B. C. D.
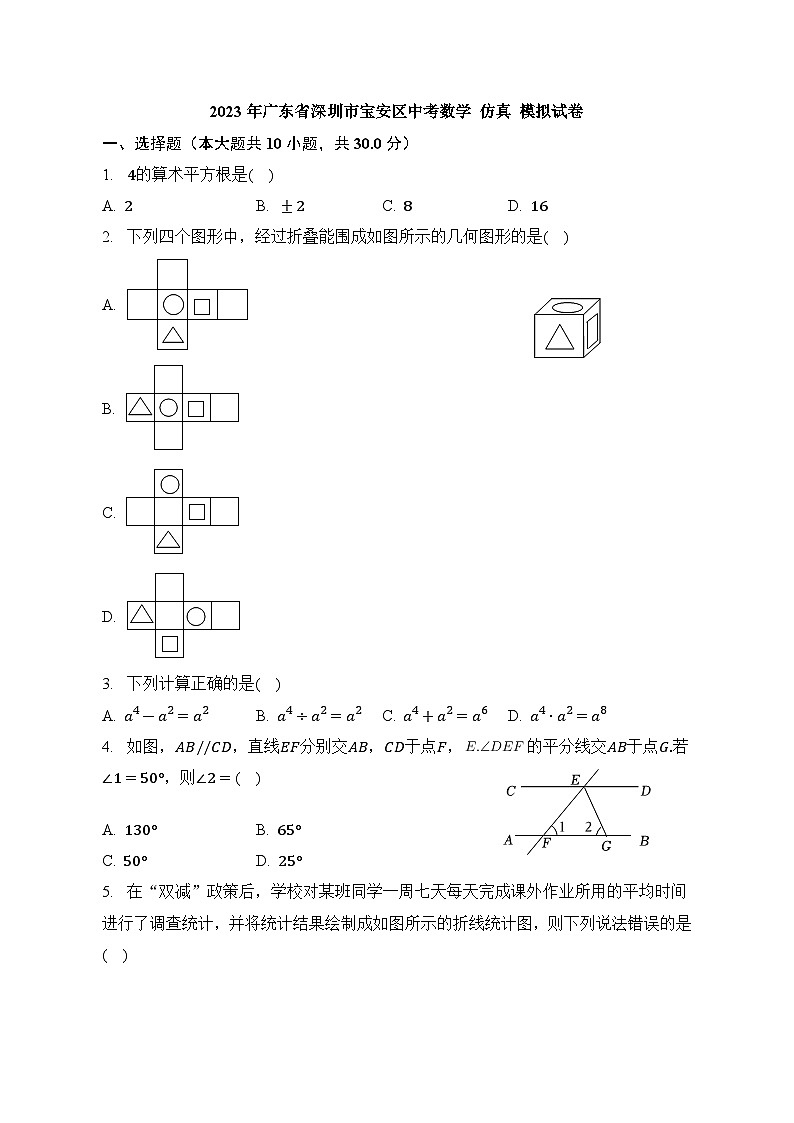
2. 下列四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
3. 下列计算正确的是( )
A. B. C. D.
4. 如图,,直线分别交,于点,的平分线交于点若,则( )
A. B.
C. D.
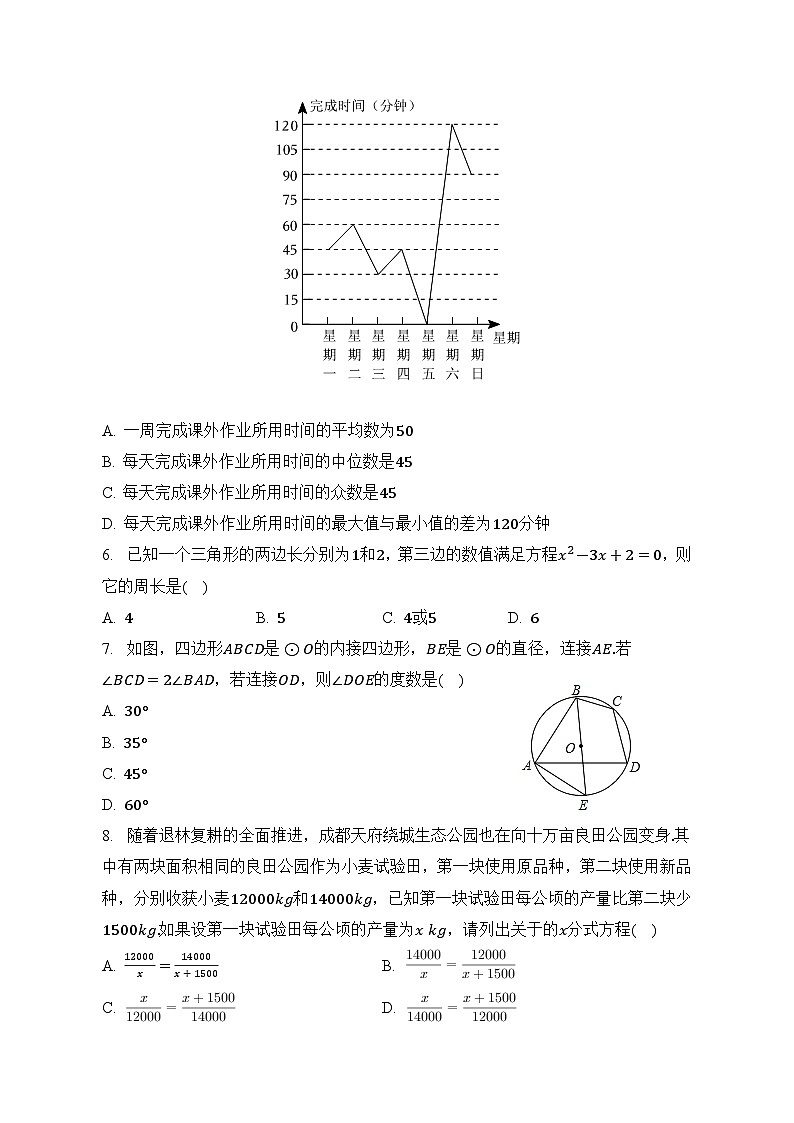
5. 在“双减”政策后,学校对某班同学一周七天每天完成课外作业所用的平均时间进行了调查统计,并将统计结果绘制成如图所示的折线统计图,则下列说法错误的是( )
A. 一周完成课外作业所用时间的平均数为
B. 每天完成课外作业所用时间的中位数是
C. 每天完成课外作业所用时间的众数是
D. 每天完成课外作业所用时间的最大值与最小值的差为分钟
6. 已知一个三角形的两边长分别为和,第三边的数值满足方程,则它的周长是( )
A. B. C. 或 D.
7. 如图,四边形是的内接四边形,是的直径,连接若,若连接,则的度数是( )
A.
B.
C.
D.
8. 随着退林复耕的全面推进,成都天府绕城生态公园也在向十万亩良田公园变身其中有两块面积相同的良田公园作为小麦试验田,第一块使用原品种,第二块使用新品种,分别收获小麦和,已知第一块试验田每公顷的产量比第二块少如果设第一块试验田每公顷的产量为,请列出关于的分式方程( )
A. B.
C. D.
9. 如图,在矩形纸片中,为上一点,将沿翻折至,若点恰好落在上,,,则( )
A.
B.
C.
D.
10. 已知二次函数是常数,图象的对称轴是直线,经过点,,且,,现有下列结论:;;;,其中正确结论的个数是( )
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
11. 年月日,“天空课堂”第三课顺利开讲,感受航天科技魅力,激发青少年探索宇宙的奥秘,其中水球变“懒”实验,当天在新华网上点击率约达到次,数据用科学记数法表示为______ .
12. 在一个不透明的盒子中,装有绿色、黑色、白色的小球共有个,除颜色外其他完全相同,一同学通过多次摸球试验后发现其中摸到绿色球、黑色球的频率稳定在和,盒子中白色球的个数可能是______ .
13. 如图,在平面直角坐标系中,一次函数和函数的图象交于、两点.利用函数图象直接写出不等式的解集是______.
14. 如图,学校有一旗杆为了测量旗杆高度,小明采用如下方案:在点处测得旗杆顶的仰角为,从与点相距的处测得旗杆顶的仰角为若,则旗杆的高度为______ 米结果保留小数点后一位,,
15. 如图,中,于点,,,,若将绕点逆时针方问旋转得到,当点恰好落在上,连接则的长是______ .
三、解答题(本大题共7小题,共55.0分。)
16. 分计算:.
17. 分先化简,再求值:,其中.
18. 分九年级某班班主任王老师为了解学生的体育锻炼情况,对本班部分学生进行了为一个月的跟踪调查,调查结果分为四类,:很好;:较好;:一般;:较差并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
王老师一共调查了多少名同学?
扇形统计图中类学生所对应的圆心角是______ 度,将上面的条形统计图补充完整;
若该校九级有学生名,估计该校学生有多少名学生体育锻炼情况是较好及以上的;
为了共同进步,王老师想从被调查的类和类学生中各随机选取一位同学进行“一帮一”,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
19. 分俄乌战争仍在继续,人们对各种军用装备倍感兴趣,某商家购进坦克模型记作和导弹记作两种模型,若购进种模型件,种模型件,需要元;若购进种模型件,种模型件,需要元.
求购进,两种模型每件分别需多少元?
若销售每件种模型可获利润元每件种模型可获利润元商店用万元购进模型,且购进种模型的数量不超过种模型数量的倍,设总盈利为元,购买种模型件,请求出关于的函数关系式,并求出当为何值时,销售利润最大,并求出最大值.
20. 分在中,,点是边上的一点,连接,作,,连接.
如图,当时,求证:;
如图,当是边的中点时,若,,求四边形的面积.
21. 分如图,抛物线与轴交于点和点,与轴交于点,顶点为,连接,,,直线与抛物线的对称轴交于点.
求抛物线的解析式和直线的解析式;
求四边形的面积;
是第一象限内抛物线上的动点,连接,,当时,求点的坐标.
22. 分如图,在菱形中,,点,分别在边,上,,,连接.
求证:是等边三角形;
如图,把沿翻折得到,连接,若,求的长;
如图,把绕点顺时针旋转得到,连接,是的中点,连接,,判断与的数量关系,并给出证明.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.解:
.
17.解:
;
当时,
原式.
18.解:(1)(1+2)÷15%=20(名),
所以李老师一共调查了20名同学;
(2)C类人数为25%×20=5(人),
所以C类的女生人数为5-2=3(名),
所以D类人数为20-3-10-5=2(名),
其中男生人数为2-1=1(名),
所以扇形统计图中D类学生所对应的圆心角为×360°=36°,
条形统计图补充为:
故答案为:36;
(3)700×(15%+50%)=455(名),
估计该校学生有455名学生体育锻炼情况是较好及以上的;
(4)画树状图为:
共有6种等可能的结果数,其中一位男同学和一位女同学的结果数为3,
所以所选两位同学恰好是一位男同学和一位女同学的概率==.
19.解:设购进,两种模型每件分别需要元,元,
由题意得:,
解得,,
答:,两种模型每件分别需要元,元.
设购买种模型件,购买种模型件,
由题意得,,
解得,,
则购买种模型为件,即件,
则,
,
当取最小值时,最大,
,取整数,
当时,.
答:;当时,利润最大为元.
20.证明:,,
四边形是平行四边形,
,
,
四边形是矩形,
;
解:是边的中点,,,
,
,,
四边形是平行四边形,
四边形是菱形,
,
,
,
四边形的面积是,
即四边形的面积是.
21.解:抛物线过点和,
,
解得,
抛物线的解析式为,
令,得,
解得,,
点的坐标为,
设直线的解析式为,
把点,分别代入,
得,
解得,
直线的解析式为;
如图,设抛物线的对称轴与轴交于点,
抛物线的解析式为,
顶点的坐标为,
;
,
,
如图,过点作轴,交轴于点,交于点.
设点,
点在直线上,
,
,
,
,
解得,,
点的坐标为或.
22.证明:如图,四边形是菱形,
,,
,,
,
是等边三角形;
解:如图,过点作的延长线于点,过点作的延长线于点,
四边形是菱形,
,
,
,,
,,
由翻折可知是等边三角形,
,,
,,
,,
,
,
,,,
,
四边形是矩形,
,,
,
;
,理由如下:
如图,把绕点顺时针旋转得到,延长交于点,连接、,
是的中点,
,
四边形是菱形,
,
,,
≌,
,,
,
由旋转可知是等边三角形,
,,
,
,
≌,
,,
,
,
是等边三角形,
,
,,
.
精品解析:2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷(一): 这是一份精品解析:2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷(一),文件包含精品解析2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷一原卷版docx、精品解析2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷一解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷(一) (原卷及解析版): 这是一份2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷(一) (原卷及解析版),文件包含2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷一原卷版pdf、2022年广东省深圳市宝安区第一外国语学校中考数学仿真试卷一解析版pdf等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
2023年广东省深圳市中考数学仿真模拟试卷(含答案): 这是一份2023年广东省深圳市中考数学仿真模拟试卷(含答案),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












