- 初中数学人教九下第二十八章卷(1) 试卷 0 次下载
- 初中数学人教九下第二十八章卷(3) 试卷 0 次下载
- 初中数学人教九下第二十八章卷(4) 试卷 0 次下载
- 初中数学人教九下第二十九章卷(1) 试卷 0 次下载
- 初中数学人教九下第二十九章卷(2) 试卷 0 次下载
初中数学人教九下第二十八章卷(2)
展开单元测试卷(二)
一、选择题(每小题3分,共 24分)
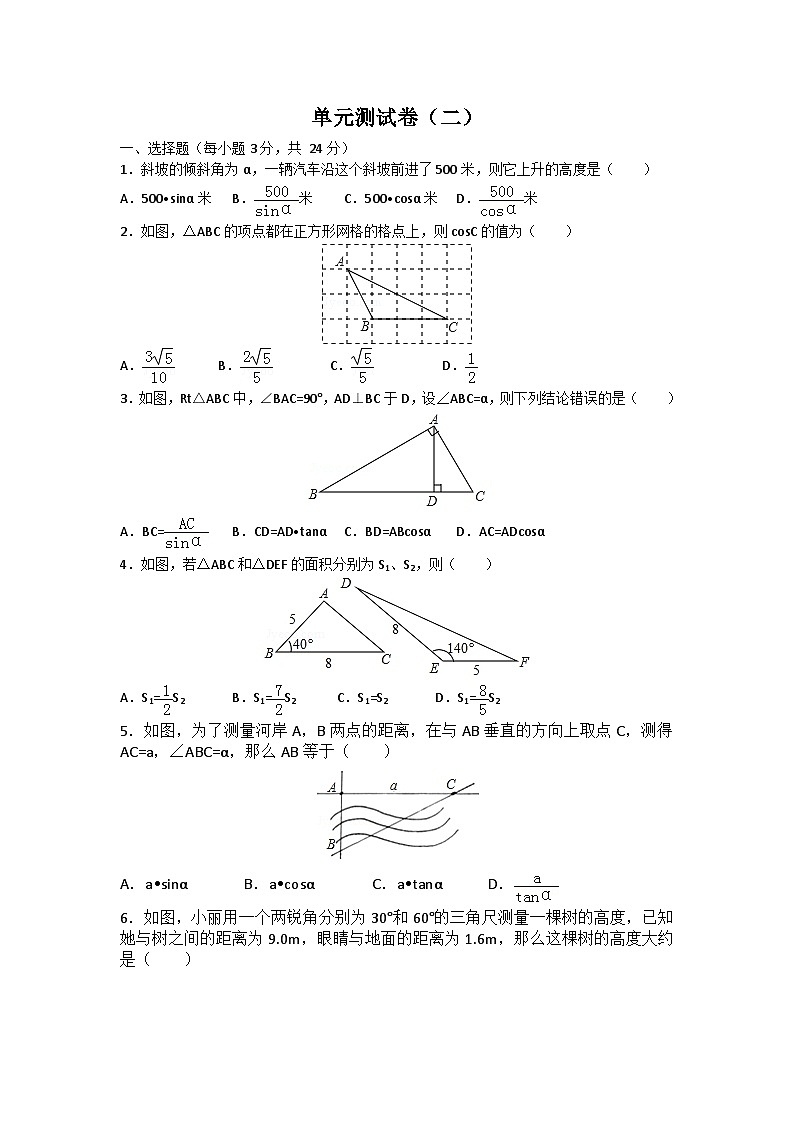
1.斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )
A.500•sinα米 B.米 C.500•cosα米 D.米
2.如图,△ABC的项点都在正方形网格的格点上,则cosC的值为( )
A. B. C. D.
3.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
A.BC= B.CD=AD•tanα C.BD=ABcosα D.AC=ADcosα
4.如图,若△ABC和△DEF的面积分别为S1、S2,则( )
A.S1=S2 B.S1=S2 C.S1=S2 D.S1=S2
5.如图,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于( )
A.a•sinα B.a•cosα C.a•tanα D.
6.如图,小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为9.0m,眼睛与地面的距离为1.6m,那么这棵树的高度大约是( )
A.5.2m B.6.8m C.9.4m D.17.2m
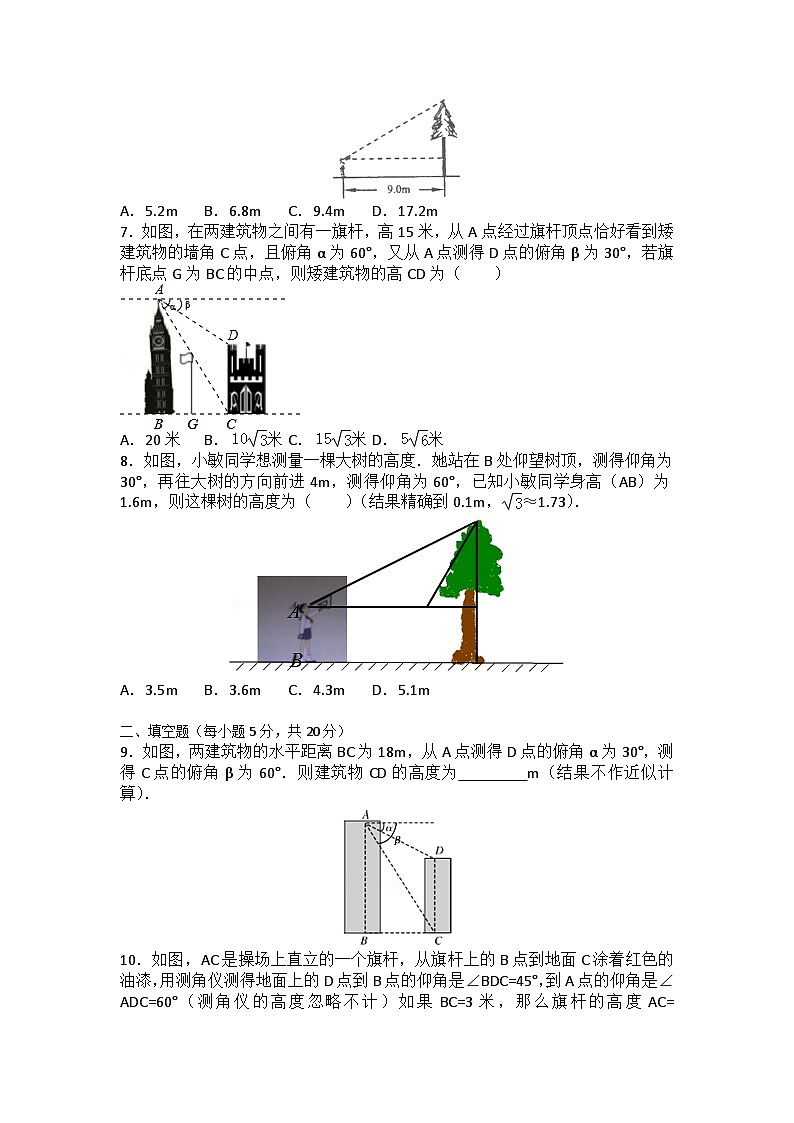
7.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.米 C.米 D.米
8.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m,≈1.73).
A.3.5m B.3.6m C.4.3m D.5.1m
二、填空题(每小题5分,共20分)
9.如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 m(结果不作近似计算).
10.如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,那么旗杆的高度AC= 米.
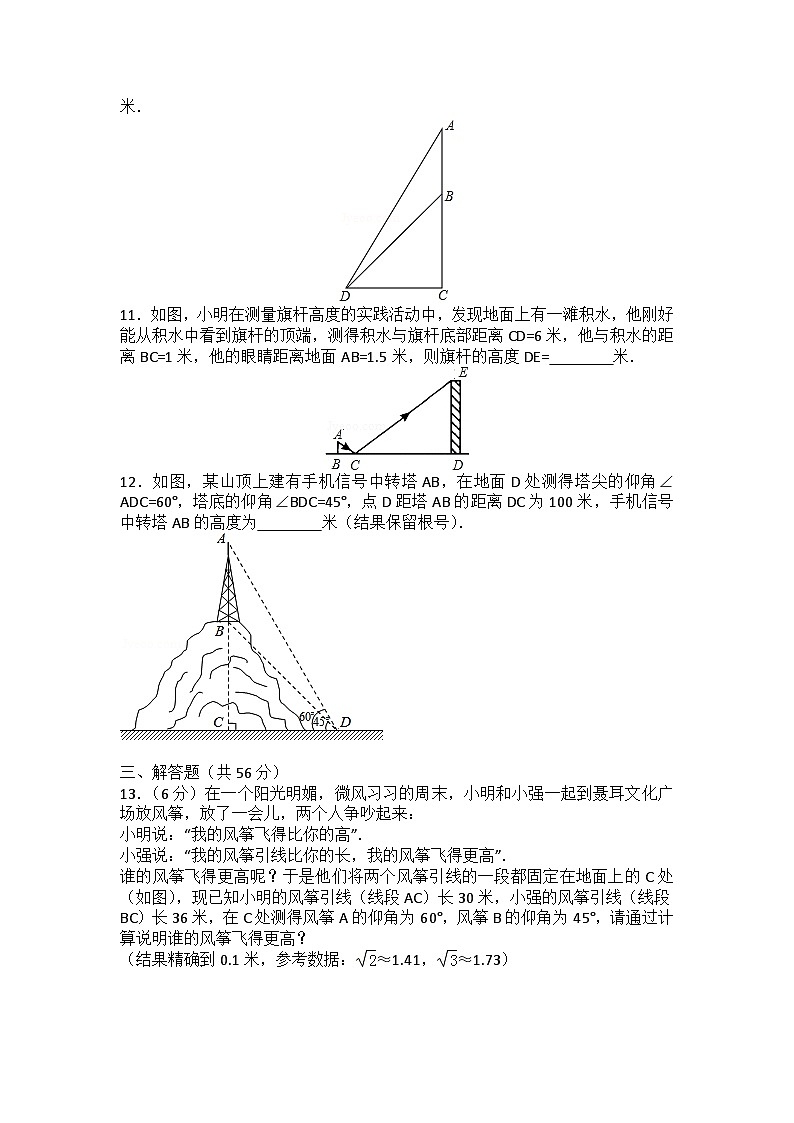
11.如图,小明在测量旗杆高度的实践活动中,发现地面上有一滩积水,他刚好能从积水中看到旗杆的顶端,测得积水与旗杆底部距离CD=6米,他与积水的距离BC=1米,他的眼睛距离地面AB=1.5米,则旗杆的高度DE= 米.
12.如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距塔AB的距离DC为100米,手机信号中转塔AB的高度为 米(结果保留根号).
三、解答题(共56分)
13.(6分)在一个阳光明媚,微风习习的周末,小明和小强一起到聂耳文化广场放风筝,放了一会儿,两个人争吵起来:
小明说:“我的风筝飞得比你的高”.
小强说:“我的风筝引线比你的长,我的风筝飞得更高”.
谁的风筝飞得更高呢?于是他们将两个风筝引线的一段都固定在地面上的C处(如图),现已知小明的风筝引线(线段AC)长30米,小强的风筝引线(线段BC)长36米,在C处测得风筝A的仰角为60°,风筝B的仰角为45°,请通过计算说明谁的风筝飞得更高?
(结果精确到0.1米,参考数据:≈1.41,≈1.73)
14.(8分)如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).
(1)若气球从Q处继续向前移动,方向不变,再过几秒位于B点正上方?
(2)求AB的长(结果保留根号).
15.(6分)在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin20°≈,cos20°≈,tan20°≈)
16.(6分)国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:=1.732,=1.414)
17.(6分)如图,小方在五月一日假期中到郊外放风筝,风筝飞到C 处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度(结果精确到个位)
18.(6分)如图,小山顶上有一信号塔AB,山坡BC的倾角为30°,现为了测量塔高AB,测量人员选择山脚C处为一测量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB(结果保留整数,≈1.73,≈1.41)
19.(8分)天塔是天津市的标志性建筑之一,某校数学兴趣小组要测量天塔的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=112m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
20.(10分)如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
答案解析
1.斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )
A.500•sinα米 B.米 C.500•cosα米 D.米
【考点】T9:解直角三角形的应用﹣坡度坡角问题.
【专题】选择题
【分析】根据题意画出图形,再利用坡角的正弦值即可求解.
【解答】解:如图,∠A=α,AE=500.
则EF=500sinα.
故选A.
【点评】此题主要考查坡度坡角问题,正确掌握坡角的定义是解题关键.
2.如图,△ABC的项点都在正方形网格的格点上,则cosC的值为( )
A. B. C. D.
【考点】T1:锐角三角函数的定义;KQ:勾股定理.
【专题】选择题
【分析】先构建格点三角形ADC,则AD=2,CD=4,根据勾股定理可计算出AC,然后根据余弦的定义求解.
【解答】解:在格点三角形ADC中,AD=2,CD=4,
∴AC===2,
∴cosC===.
故选B.
【点评】本题考查了锐角三角函数的定义:在直角三角形中,一锐角的余弦等于它的邻边与斜边的比值.也考查了勾股定理.
3.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
A.BC= B.CD=AD•tanα C.BD=ABcosα D.AC=ADcosα
【考点】T7:解直角三角形.
【专题】选择题
【分析】在直角三角形中利用锐角三角函数求角边关系即可.
【解答】解:A.在Rt△ABC中,sinα=,
∴BC=,故A正确;
B.∵∠B+∠BAD=90°,∠CAD+∠BAD=90°,
∴∠B=∠CAD=α,
在Rt△ADC中,tanα=,
∴CD=AD•tanα,
故B正确;
C.在Rt△ABD中,
cosα=,
∴BD=AB•cosα,
故C正确;
D.在Rt△ADC中,cosα=,
∴AD=AC•cosα,
故D错误;
故选D.
【点评】本题主要考查了直角三角形角边关系,熟练掌握边角之间的关系:sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边)是解答此题的关键.
4.如图,若△ABC和△DEF的面积分别为S1、S2,则( )
A.S1=S2 B.S1=S2 C.S1=S2 D.S1=S2
【考点】T7:解直角三角形;K3:三角形的面积.
【专题】选择题
【分析】过A点作AG⊥BC于G,过D点作DH⊥EF于H.在Rt△ABG中,根据三角函数可求AG,在Rt△ABG中,根据三角函数可求DH,根据三角形面积公式可得S1,S2,依此即可作出选择.
【解答】解:过A点作AG⊥BC于G,过D点作DH⊥EF于H.
在Rt△ABG中,AG=AB•sin40°=5sin40°,
∠DEH=180°﹣140°=40°,
在Rt△DHE中,DH=DE•sin40°=8sin40°,
S1=8×5sin40°÷2=20sin40°,
S2=5×8sin40°÷2=20sin40°.
则S1=S2.
故选C.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系,关键是作出高线构造直角三角形.
5.如图,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于( )
A.a•sinα B.a•cosα C.a•tanα D.
【考点】T8:解直角三角形的应用.
【专题】选择题
【分析】根据已知角的正切值表示即可.
【解答】解:∵AC=a,∠ABC=α,在直角△ABC中tanα=,
∴AB=.
故选D.
【点评】此题主要考查了解直角三角形的应用,正确记忆三角函数的定义是解决本题的关键.
6.如图,小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为9.0m,眼睛与地面的距离为1.6m,那么这棵树的高度大约是( )
A.5.2m B.6.8m C.9.4m D.17.2m
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【专题】选择题
【分析】三角尺和树构成直角三角形,根据一直角边和三角尺的度数,可将眼睛到树尖的距离求出,加上眼睛与地面的距离即为这棵树的高度.
【解答】解:由图中所示:眼睛到树尖的距离h1=tan30°×9=,
眼睛与地面之间的距离:h2=1.6,
∴这棵树的高度h=h1+h2=3+1.6≈6.8(m).
故选B.
【点评】本题主要是将实际问题与解直角三角形联系起来,使求解过程变得简单.
7.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.米 C.米 D.米
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】根据点G是BC中点,可判断EG是△ABC的中位线,求出AB,在Rt△ABC中求出BC,在Rt△AFD中求出DF,继而可求出CD的长度.
【解答】解:∵点G是BC中点,EG∥AB,
∴EG是△ABC的中位线,
∴AB=2EG=30米,
在Rt△ABC中,∠CAB=30°,
则BC=ABtan∠BAC=30×=10米.
如图,过点D作DF⊥AF于点F.
在Rt△AFD中,AF=BC=10米,
则FD=AF•tanβ=10×=10米,
综上可得:CD=AB﹣FD=30﹣10=20米.
故选:A.
【点评】本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.
8.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m,≈1.73).
A.3.5m B.3.6m C.4.3m D.5.1m
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【专题】12 :应用题.
【分析】设CD=x,在Rt△ACD中求出AD,在Rt△CED中求出ED,再由AE=4m,可求出x的值,再由树高=CD+FD即可得出答案.
【解答】解:设CD=x,
在Rt△ACD中,CD=x,∠CAD=30°,
则tan30°=CD:AD=x:AD
故AD=x,
在Rt△CED中,CD=x,∠CED=60°,
则tan60°=CD:ED=x:ED
故ED=x,
由题意得,AD﹣ED=x﹣x=4,
解得:x=2,
则这棵树的高度=2+1.6≈5.1m.
故选D.
【点评】本题考查了解直角三角形的应用,解答本题关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度.
9.如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 12 m(结果不作近似计算).
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】首先过点D作DE⊥AB于点E,可得四边形BCDE是矩形,然后分别在Rt△ABC与Rt△ADE中,利用正切函数的知识,求得AB与AE的长,继而可求得答案.
【解答】解:过点D作DE⊥AB于点E,
则四边形BCDE是矩形,
根据题意得:∠ACB=β=60°,∠ADE=α=30°,BC=18m,
∴DE=BC=18m,CD=BE,
在Rt△ABC中,AB=BC•tan∠ACB=18×tan60°=18(m),
在Rt△ADE中,AE=DE•tan∠ADE=18×tan30°=6(m),
∴DC=BE=AB﹣AE=18﹣6=12(m).
故答案为:12.
【点评】本题考查俯角的知识.此题难度不大,注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想的应用.
10.如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,那么旗杆的高度AC= 3 米.
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【专题】12 :应用题.
【分析】在Rt△BDC中,根据∠BDC=45°,求出DC=BC=3米,在Rt△ADC中,根据∠ADC=60°即可求出AC的高度.
【解答】解:在Rt△BDC中,
∵∠BDC=45°,
∴DC=BC=3米,
在Rt△ADC中,
∵∠ADC=60°,
∴AC=DCtan60°=3×=3(米).
故答案为:3.
【点评】本题考查了解直角三角形的应用,解题的关键是根据仰角构造直角三角形,解直角三角形,难度一般.
11.如图,小明在测量旗杆高度的实践活动中,发现地面上有一滩积水,他刚好能从积水中看到旗杆的顶端,测得积水与旗杆底部距离CD=6米,他与积水的距离BC=1米,他的眼睛距离地面AB=1.5米,则旗杆的高度DE= 9 米.
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】先根据光的反射定律得出∠ACB=∠ECD,再得出Rt△ACB∽Rt△ECD,根据相似三角形对应边成比例即可得出结论.
【解答】解:根据光的反射定律,∠ACB=∠ECD,
∵∠ACB=∠EDC,CD=6米,AB=1.5米,BC=1米,
∴Rt△ACB∽Rt△ECD,
∴=,即=,解得DE=9.
故答案为:9.
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,熟知相似三角形的对应边成比例是解答此题的关键.
12.如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距塔AB的距离DC为100米,手机信号中转塔AB的高度为 米(结果保留根号).
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】先在Rt△BCD中,根据∠BDC=45°,得出BC=CD=100;再在Rt△ACD中,根据正切函数的定义,求出AC=100,然后由AB=AC﹣BC即可求解.
【解答】解:由题意可知,△ACD与△BCD都是直角三角形.
在Rt△BCD中,∵∠BDC=45°,
∴BC=CD=100.
在Rt△ACD中,∵∠ADC=60°,CD=100,
∴tan∠ADC=,即,
∴,
∴AB=AC﹣BC=.
答:手机信号中转塔的高度为米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,难度适中,解答本题的关键是借助仰角构造直角三角形并解直角三角形.
13.在一个阳光明媚,微风习习的周末,小明和小强一起到聂耳文化广场放风筝,放了一会儿,两个人争吵起来:
小明说:“我的风筝飞得比你的高”.
小强说:“我的风筝引线比你的长,我的风筝飞得更高”.
谁的风筝飞得更高呢?于是他们将两个风筝引线的一段都固定在地面上的C处(如图),现已知小明的风筝引线(线段AC)长30米,小强的风筝引线(线段BC)长36米,在C处测得风筝A的仰角为60°,风筝B的仰角为45°,请通过计算说明谁的风筝飞得更高?
(结果精确到0.1米,参考数据:≈1.41,≈1.73)
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】在Rt△ACD和Rt△BCE中,分别解直角三角形,求得AD和BE的高度,比较即可.
【解答】解:分别过A,B作地面的垂线,垂足分别为D,E,
在Rt△ACD中,
∵sin∠ACD=,
∴AD=AC•sin∠ACD=30×sin60°=15≈26.0(米).
在Rt△BCE中,
∵sin∠BCE=,
∴BE=BC•sin∠BCE=36×sin45°=18≈25.4(米).
∵26.0>25.4,
∴小明的风筝飞得更高.
【点评】本题考查了解直角三角形的应用,要求学生能借助仰角构造直角三角形并解直角三角形.
14.如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).
(1)若气球从Q处继续向前移动,方向不变,再过几秒位于B点正上方?
(2)求AB的长(结果保留根号).
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】(1)首先过点B作BH⊥PQ,垂足为H,即可得出QH=HB=90m,进而利用平移速度得出答案;
(2)首先过点P作PE⊥AB,垂足为E,利用tan60°===,进而得出AE的长,再利用PH=BE进而得出AB的长.
【解答】解:(1)过点B作BH⊥PQ,垂足为H,
∵一热气球在距地面90米高的P处,
∴HB=90m,
∵∠HQB=45°,
∴∠2=45°,
∴QH=HB=90m,
∴90÷9=10(秒),
答:气球从Q处继续向前移动,方向不变,再过10秒位于B点正上方;
(2)过点P作PE⊥AB,垂足为E,
∵一热气球在距地面90米高的P处,
∴PE=90m,
∵∠QPA=60°,
∴∠1=60°,
∴tan60°===,
∴AE==30,
∵气球以每秒9米的速度沿AB方向移动,5秒到达Q处,
∴PQ=5×9=45(m),
∴PH=45+90=135(m),
∴BE=135(m),
∴AB=BE﹣AE=(135﹣30)m,
答:AB的长为(135﹣30)m.
【点评】此题主要考查了仰角与俯角的应用,根据题意得出直角三角形利用已知角度得出HQ的长是解题关键.
15.在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin20°≈,cos20°≈,tan20°≈)
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】设AB=x,则BC=x,DB=20+x,在Rt△△ABD中利用20°的锐角三角函数值即可求出BC的长,又因为AM=AB+BM,问题得解.
【解答】解:由题意得∠ABC=90°
∵∠ACB=45°
∴∠CAB=90°﹣∠ACB=90°﹣45°=45°
∴AB=BC
设AB=x,则BC=x,DB=20+x
在Rt△ABD中
∵tan∠ADB=
∴tan20°=,
∵tan20°≈,
∴,
x=11.25
∵BM=CE=1.5
∴AM=11.25+1.5=12.75
答:教学楼的高AM是12.75米.
方法二
解:设BD为x,则BC=x﹣20
∵∠ACB=45°,∠ABC=90°
∴∠CAB=45°
∴AB=BC=x﹣20
在Rt△ABD中
∵tan∠ADB=,
∴tan20°=,
∵tan20°=,
∴,
x=31.25
∴BC=31.25﹣20=11.25
∵BM=CE=1.5
∴AM=11.25+1.5=12.75.
答:教学楼的高AM约为12.75米.
【点评】本题考查了解直角三角形的应用,构造仰角所在的直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.
16.国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:=1.732,=1.414)
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】设CF=x,在Rt△ACF和Rt△BCF中,分别用CF表示AC、BC的长度,然后根据AC﹣BC=1200,求得x的值,用h﹣x即可求得最高海拔.
【解答】解:设CF=x,
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x,
=tan30°,
即AC=x,
∵AC﹣BC=1200米,
∴x﹣x=1200,
解得:x=600(+1),
则DF=h﹣x=2001﹣600(+1)≈362(米).
答:钓鱼岛的最高海拔高度约362米.
【点评】本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形求出AC、BC的长度,难度一般.
17.如图,小方在五月一日假期中到郊外放风筝,风筝飞到C 处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度(结果精确到个位)
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】易得DE=AB,利用BC长和60°的正弦值即可求得CD长,加上DE长就是此时风筝离地面的高度.
【解答】解:依题意得,∠CDB=∠BAE=∠ABD=∠AED=90°,
∴四边形ABDE是矩形,(1分)
∴DE=AB=1.5,(2分)
在Rt△BCD中,,(3分)
又∵BC=20,∠CBD=60°,
∴CD=BC•sin60°=20×=10,(4分)
∴CE=10+1.5≈19米,(5分)
答:此时风筝离地面的高度约为19米.
【点评】考查仰角的定义,能借助仰角构造直角三角形并解直角三角形是仰角问题常用的方法.
18.如图,小山顶上有一信号塔AB,山坡BC的倾角为30°,现为了测量塔高AB,测量人员选择山脚C处为一测量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB(结果保留整数,≈1.73,≈1.41)
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【专题】12 :应用题.
【分析】先判断△ACE为等腰三角形,在Rt△AEF中表示出EF、AF,在Rt△BEF中求出BF,根据AB=AF﹣BF即可得出答案.
【解答】解:依题意可得:∠AEB=∠EAB=30°,∠ACE=15°,
又∵∠AEB=∠ACE+∠CAE
∴∠CAE=15°,
即△ACE为等腰三角形,
∴AE=CE=100m,
在Rt△AEF中,∠AEF=60°,
∴EF=AEcos60°=50m,AF=AEsin60°=50m,
在Rt△BEF中,∠BEF=30°,
∴BF=EFtan30°=50×=m,
∴AB=AF﹣BF=50﹣=≈58(米).
答:塔高AB大约为58米.
【点评】本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度,难度一般.
19.天塔是天津市的标志性建筑之一,某校数学兴趣小组要测量天塔的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=112m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【分析】首先根据题意得:∠CAD=45°,∠CBD=54°,AB=112m,在Rt△ACD中,易求得BD=AD﹣AB=CD﹣112;在Rt△BCD中,可得BD=CD•tan36°,即可得CD•tan36°=CD﹣112,继而求得答案.
【解答】解:根据题意得:∠CAD=45°,∠CBD=54°,AB=112m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD﹣AB=CD﹣112(m),
∵在Rt△BCD中,tan∠BCD=,∠BCD=90°﹣∠CBD=36°,
∴tan36°=,
∴BD=CD•tan36°,
∴CD•tan36°=CD﹣112,
∴CD=≈≈415(m).
答:天塔的高度CD约为:415m.
【点评】本题考查了仰角的知识.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.
20.如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
【考点】TA:解直角三角形的应用﹣仰角俯角问题.
【专题】12 :应用题.
【分析】(1)根据猫头鹰从C点观测F点的俯角为53°,可知∠DFG=90°﹣53°=37°,在△DFG中,已知DF的长度,求出DG的长度,若DG>3,则看不见老鼠,若DG<3,则可以看见老鼠;
(2)根据(1)求出的DG长度,求出AG的长度,然后在Rt△CAG中,根据=sin∠ACG=sin37°,即可求出CG的长度.
【解答】解:(1)能看到;
由题意得,∠DFG=90°﹣53°=37°,
则=tan∠DFG,
∵DF=4米,
∴DG=4×tan37°≈4×0.75=3(米),
故能看到这只老鼠;
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又=sin∠ACG=sin37°,
则CG=≈=9.5(米).
答:要捕捉到这只老鼠,猫头鹰至少要飞约9.5米.
【点评】本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形并解直角三角形,利用三角函数求解相关线段,难度一般.
初中数学人教九下第二十八章卷2: 这是一份初中数学人教九下第二十八章卷2,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学人教九下第二十八章卷1: 这是一份初中数学人教九下第二十八章卷1,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学人教九下第二十八章达标检测卷: 这是一份初中数学人教九下第二十八章达标检测卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












