数学人教版7年级下册期末复习专题卷 01

·人教版·

数学

数学人教版7年级下册期末复习专题卷

01 相交与平行

一、单选题

1．如图，由下列已知条件推出的结论中，正确的是（    ）

A．由，可以推出

B．由，可以推出

C．由，可以推出

D．由是的余角，分别平分和，可以推出

2．将直尺和直角三角板按如图所示方式摆放，已知，则的大小是（   ）

A． B． C． D．

3．在下列命题中，为真命题的是（   ）

A．相等的角是对顶角 B．平行于同一条直线的两条直线互相平行

C．同旁内角互补 D．垂直于同一条直线的两条直线互相垂直

4．如图，，，，则的度数是（　　）

A．  B．  C．  D．

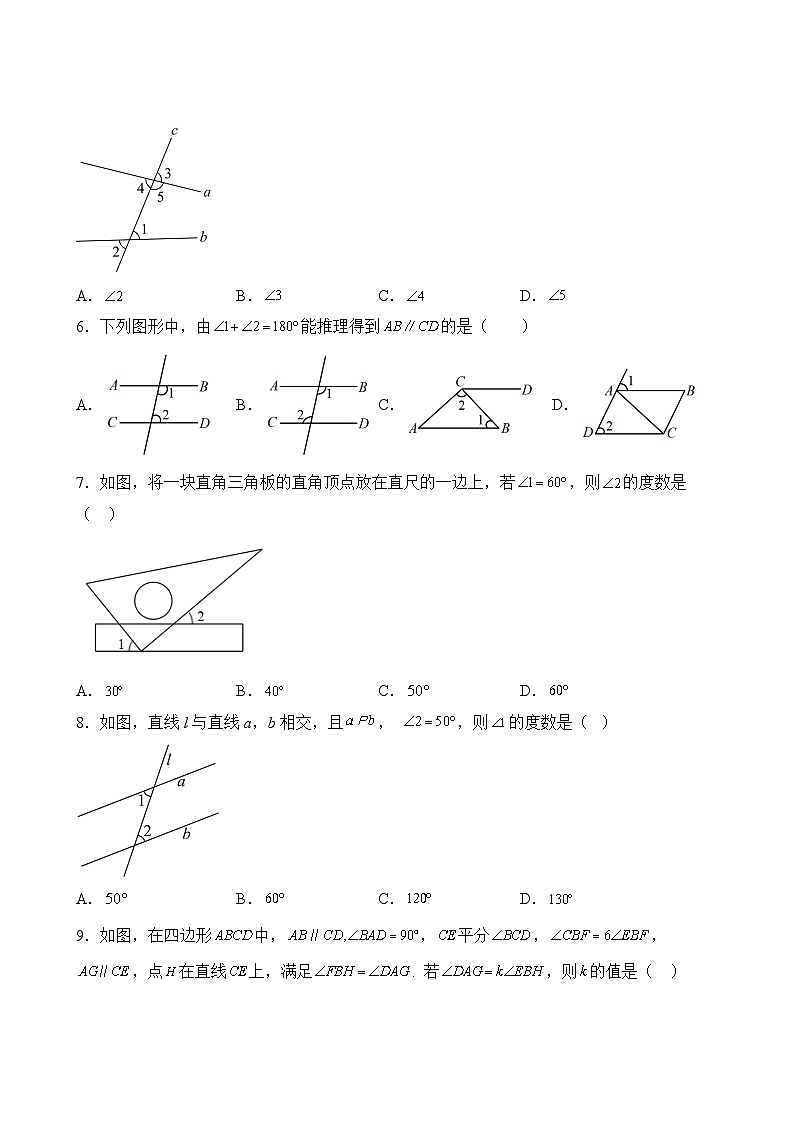
5．如图，直线a，b被直线c所截，则的同位角是（   ）

A． B． C． D．

6．下列图形中，由能推理得到的是（　　）

A． B． C． D．

7．如图，将一块直角三角板的直角顶点放在直尺的一边上，若，则的度数是（    ）

A． B． C． D．

8．如图，直线l与直线a，b相交，且， ，则的度数是（   ）

A． B． C． D．

9．如图，在四边形中，，平分，，，点在直线上，满足. 若，则的值是（    ）

A．和 B．和 C．和 D．和

10．数学课上老师用双手形象的表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）．从左至右依次表示（     ）

A．同位角、内错角、同旁内角 B．同旁内角、同位角、内错角

C．同位角、对顶角、同旁内角 D．同位角、内错角、对顶角

11．如图，点在的延长线上，下列条件中不能判定的是（        ）

A． B． C． D．

12．如图，把一块含有角的直角三角板的两个顶点放在直尺的对边上，如果，那么的度数是（　　）

A． B． C． D．

13．如图，直线，且a，b被直线c所截．若，则∠2的大小为（    ）

A． B． C． D．

二、填空题

14．如图，下列条件：①；②；③；④，能判定的是_____（填写正确答案的序号）．

15．如图，已知在中，，，则的度数为____________．

16．如图，直线，将一个直角的顶点放在直线上，若，则_____．

17．将一个直角三角板和一把直尺如图放置，如果，那么的度数为______．

18．某兴趣小组利用几何图形画出螳螂的简笔画，如图，已知，，，则________°．

19．如图，点B、C、E在同一条直线上，请你写出一个能使成立的条件：______．（只写一个即可，不添加任何字母或数字）

20．将一副三角板中的两块直角三角尺的直角顶点按如图方式叠放在一起，其中，，，当，且点在直线的上方时，若这两块三角尺有两条边平行，则______

21．如图，将三角形沿方向平移得到三角形，若三角形的周长为，则四边形的周长为________．

22．如图，，，则____．

23．沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反，若汽车第一次是右拐，则第二次应该是右拐______ 度

24．如图，请添加一个条件，使得，则符合要求的其中一个条件可以是______________.

25．推理填空：如图，已知，，可推得．理由如下：

∵（已知），且（　          　）

∴（等量代换）

∴（　                  　）

∴（                         ）

又∵（已知），

∴（等量代换）

∴（　                   　）

26．如图，，，于，则的度数是______度．

27．如图，直线分别与直线，相交于点G，H，且．点M在直线，之间，连接，，射线是的平分线，在的延长线上取点N，连接，若，，则的度数为_____．

28．如图于点D，将绕点A逆时针旋转，使，则的最小值为___．

三、解答题

29．如图，已知两条射线，动线段的两个端点A、B分别在射线、上，且，F在线段上，平分，平分．

(1)证明：；

(2)若平行移动，那么与的度数比是否随着位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；

(3)在平行移动的过程中，若，求．

30．如图，直线与相交于点，，．

(1)图中的余角有________；（把符合条件的角都填出来）

(2)，求的度数．

31．已知：如图，，，，求的度数

32．已知：点为直线上一点，过点作射线，．

(1)如图1，求的度数；

(2)如图2，过点作射线，使，作的平分线，求的度数：

(3)如图3，在（2）的条件下，作射线，若与互余，请画出图形，并求的度数．

33．如图，已知，，点P是射线上一动点（与点A不重合），，分别平分和，分别交射线于点C，D．

(1)求的度数；

(2)当点P运动时，的比值是否随之变化？若不变，请求出这个比值；若变化，请找出变化规律；

(3)当点P运动到某处时，，求此时的度数．

34．如图，已知，，．求证：．

证明：∵，（已知），

又∵ （ ），

∴ （ ）．

∴ （ ）．

∴（ ）．

∵，（已知）

∴．

∴（ ）．

35．如图，，平分．

(1)求证：；

(2)求的度数．

36．如图，在四边形中，E、F分别是、延长线上的点，连接，分别交、于点G、H．若，，试说明．请根据题意填空：

解：因为（已知）

（ ）

所以（ ）

所以   （ ）

所以（ ）

因为（已知）

所以 ．

所以（ ）

37．已知，分别与交于，点是上的定点，点是直线上一动点（点不与点重合），

(1)如图1，若，，求的度数．

(2)点在运动的过程中，探究，和的数量关系，并说明理由．

38．如图，已知，，试证明．完成以下解答过程中的空缺部分；

解：∵（已知）

∴（       ）

∴  （等量代换）

∴（        ）

∴（      ）

∵（已知）

∴（        ）

∴___________（内错角相等，两直线平行）

39．如图，，，试判断与的大小关系，并说明理由．

解：相等，理由如下：

（已知），（邻补角定义），

（____________________），

（____________________），

（____________________），

又（已知），

________（等量代换），

（____________________），

（____________________）．

40．请把下列的证明过程补充完整；

如图，点、在上，点、分别在、上，，．求证：．

证明：（已知），

__________（同位角相等，两直线平行）

（_________________），

（已知），

__________（同角的补角相等），

（_______________），

（_______________），

（垂直定义）．

41．完成下面的证明．

已知：如图，，．求证：．

证明：∵（已知），

∴ （  ）．

∴ （  ）．

∵（已知），（  ）．

∴（等量代换）．

∴（同位角相等，两直线平行），

∴（ ）．

∴（等量代换）．

参考答案

1．D

2．C

3．B

4．B

5．B

6．A

7．A

8．A

9．C

10．A

11．C

12．D

13．C

14．①②/②①

15．/120度

16．/40度

17．/度

18．20

19．（答案不唯一）

20．或

21．26

22．/128度

23．70

24．（或答案不唯一）

25．对顶角相等；同位角相等，两直线平行；内错角相等，两直线平行

26．30

27．/45度

28．/25度

29．（1）∵，

∴，

∵，

∴，

∴，

∴，

∵，

∴，

∴；

（2）不变，理由如下；

∵，

∴，，

∵平分，

∴，

∴；

（3）∵，

∴，

即，

∵由（1）得，

∴，

∴，

∵平分，平分，

∴，，

∴，

∵，

∴，

∵，，

∴，

∴．

30．（1）解：∵，

∴，

∵，

∴，

又，

∴，

∴的余角有，，；

（2）解：设，则，

∵，都是的余角，

∴，

∵，

∴，

∴，

即．

31．解∶过点C作，

∵，

∴，，

∴，

又，，

∴，，

∴．

32．（1）∵，

∴；

（2）由（1）得，

∵，

∴，

∵是的平分线，

∵，

∴；

（3）由（2）知，

∵与互余，

∴，

∴，

①当射线在内部时，如图（图3）1，

；

②当射线在外部时，如（图3），

．

综上所述，的度数为或．

33．（1）解：∵，

∴，

∵，分别平分和，

∴．

（2）解：不变．理由如下：

∵ ，

∴，，

又∵ 平分，

∴ ，

即的比值是2．

（3）解 ：∵，

∴，

∵，

∴ ，

∴，

∴ ，

∴ ．

34．解：∵，（已知），

又∵（对顶角相等），

∴（等量代换）．

∴（内错角相等，两直线平行）．

∴（两直线平行，同位角相等）．

∵，（已知）

∴．

∴（内错角相等，两直线平行）．

35．（1）∵，

∴，

∵，

∴，

∴．

（2）∵，

∴，

∵平分，

∴，

又∵，

∴，

∴．

36．解：因为（已知），

（对顶角相等），

所以（等量代换），

所以（同位角相等，两直线平行），

所以（两直线平行，同位角相等），

因为（已知），

所以，

所以（内错角相等，两直线平行），

故答案为：对顶角相等；等量代换；；；同位角相等，两直线平行；两直线平行，同位角相等；；内错角相等，两直线平行．

37．（1）解：如图所示，过点作，，，

∵，

∴，

∴，

∴，

∴，

∴的度数为．

（2）解：①如图所示，点在点的左边时，

由（1）的证明可知，过点作，得，

∴，且，，

∴；

②如图所示，点在点的右边时，过点作，得，

∴，

∵（对顶角相等），

∴，

∵，，

∴；

综上所示，点在点的左边时，；点在点的右边时，．

38．解：∵（已知）

∴（对顶角相等）

∴（等量代换）

∴（同旁内角互补，两直线平行）

∴（两直线平行，同位角相等）

∵（已知）

∴（等量代换）

∴（内错角相等，两直线平行）

39．解：（已知），（邻补角定义），

（同角的补角相等），

（内错角相等，两直线平行），

（两直线平行，内错角相等），

又（已知），

（等量代换），

（同位角相等，两直线平行），

（两直线平行，同位角相等）．

故答案为：同角的补角相等；内错角相等，两直线平行；两直线平行，内错角相等；；同位角相等，两直线平行；两直线平行，同位角相等

40．（已知），

（同位角相等，两直线平行）

（两直线平行，同旁内角互补），

（已知），

（同角的补角相等），

（内错角相等，两直线平行），

（两直线平行，同位角相等），

（垂直定义）．

41．∵（已知），

∴（内错角相等，两直线平行），

∴（两直线平行，内错角相等），

∵（已知），（对顶角相等），

∴（等量代换），

∴（同位角相等，两直线平行），

∴（两直线平行，同位角相等）．

∴（等量代换），

故答案为：；内错角相等，两直线平行；；两直线平行，内错角相等；对顶角相等；两直线平行，同位角相等．