

2023年河南省郑州市+中招第二次适应性测试数学试题(含答案)
展开郑州市2023年中招第二次适应性测试数学试题卷
一、选择题(每小题3分,共30分)
1. -3的绝对值是( )
A.-3 B. C.3 D.±3
2. 2023年3月30日郑州市人民公园第二十六届郁金香花展盛大开幕,据了解,本次花展共展出郁金香31个品种10万余株,采取全园分布,让游人闻着浓郁的花香,漫步于花田小径间,体验“人在花中走,如在画中游”的美妙感受.数据“10万”用科学记数法表示为( )
A.10×104 B.10×105 C.1×104 D.1×105
3. 郑州是华夏文明的重要发祥地,是三皇五帝活动的腹地,是中华文明的轴心区,市政府开展了“游郑州 知华夏”活动.将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“郑”字所在面相对的面上的汉字是( )
A.知 B.华 C.夏 D.游
4. 某校开展了丰富多彩的学雷锋志愿服务活动,为了了解同学们所做志愿者服务活动的情况,数学兴趣小组的同学在全校范围内随机抽查了部分同学,将收集的数据绘制成了如图所示的扇形统计图,若该校有2 000名学生,则参加爱心捐助活动的学生人数为( )
A.200 B.300 C.400 D.500
第4题图 第5题图
5. 如图,一副三角尺按如图所示的方式放置,若AB∥CD,则∠α的度数为( )
A.75° B.90° C.105° D.120°
6. 一元二次方程x2-2x+3=0的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.只有一个实数根
7. 凸透镜成像的原理如图所示,AG∥l∥HC.若缩小的实像是物体的,则物体到焦点F1的距离与焦点F2到凸透镜的中心线GH的距离之比为(焦点F1和F2关于O点对称)( )
A. B. C.2 D.
8. 如图,已知点A(2,a)在反比例函数的图象上,过点A作AB⊥x轴,垂足为B,连接OA,将△AOB沿OA翻折,点B的对应点B′恰好落在(k≠0)的图象上,则k的值为( )
A. B.- C.2 D.-2
9. 如图,在平面直角坐标系中,边长为2的等边三角形AOP在第二象限,OA与x轴重合,将△AOP绕点O顺时针旋转60°,得到△A1OP1,再作△A1OP1关于原点O的中心对称图形,得到△A2OP2,再将△A2OP2绕点O顺时针旋转60°,得到△A3OP3,再作△A3OP3关于原点O的中心对称图形,得到△A4OP4,以此类推……,则点P2023的坐标是( )
A.(1,) B.(-1,-) C.(2,0) D.(-2,0)
10. 已知抛物线y=x2-2mx+m2-9(m为常数)与x轴交于点A,B,点P(m+1,y1),Q(m-3,y2)为抛物线上的两点,则下列说法不正确的是( )
A.y有最小值为m2-9 B.线段AB的长为6
C.当x<m-1时,y随x的增大而减小 D.y1<y2
二、填空题(每小题3分,共15分)
11. 写出一个比0大且比3小的无理数:____________.
12. 方程的解为____________.
13. 对一批运动鞋进行抽检,统计合格的运动鞋的数量,得到合格运动鞋的频数表如下:
估计出厂的1 500双运动鞋中,次品大约有__________双.
14. 某校无人机社团的同学用无人机测量学校旗杆的高度,组员操作无人机飞至离地面高度为25米的A处时,测得旗杆BC的顶端B的俯角为45°,然后操控无人机水平方向飞行20米至旗杆另一侧D处时,测得旗杆BC的顶端B的俯角为30°,已知A,B,C,D在同一平面内,则旗杆的高度为____________米.
第14题图 第15题图
15. 黄金分割比是让无数科学家、数学家、艺术家为之着迷的数字.黄金矩形的长宽之比为黄金分割比,即矩形的短边为长边的倍.黄金分割比能够给画面带来美感,令人愉悦,在很多艺术品以及大自然中都能找到它.比如蜗牛壳的螺旋中就隐藏了黄金分割比.如下图,用黄金矩形ABCD框住整个蜗牛壳,之后作正方形ABFE,得到黄金矩形CDEF,再作正方形DEGH,得到黄金矩形CFGH……,这样作下去,我们以每个小正方形边长为半径画弧线,然后连接起来,就是黄金螺旋.已知,则阴影部分的面积为_________.
三、解答题(本大题共8个小题,满分75分)
16. (1)(5分)计算: ;
(2)(5分)解不等式组:.
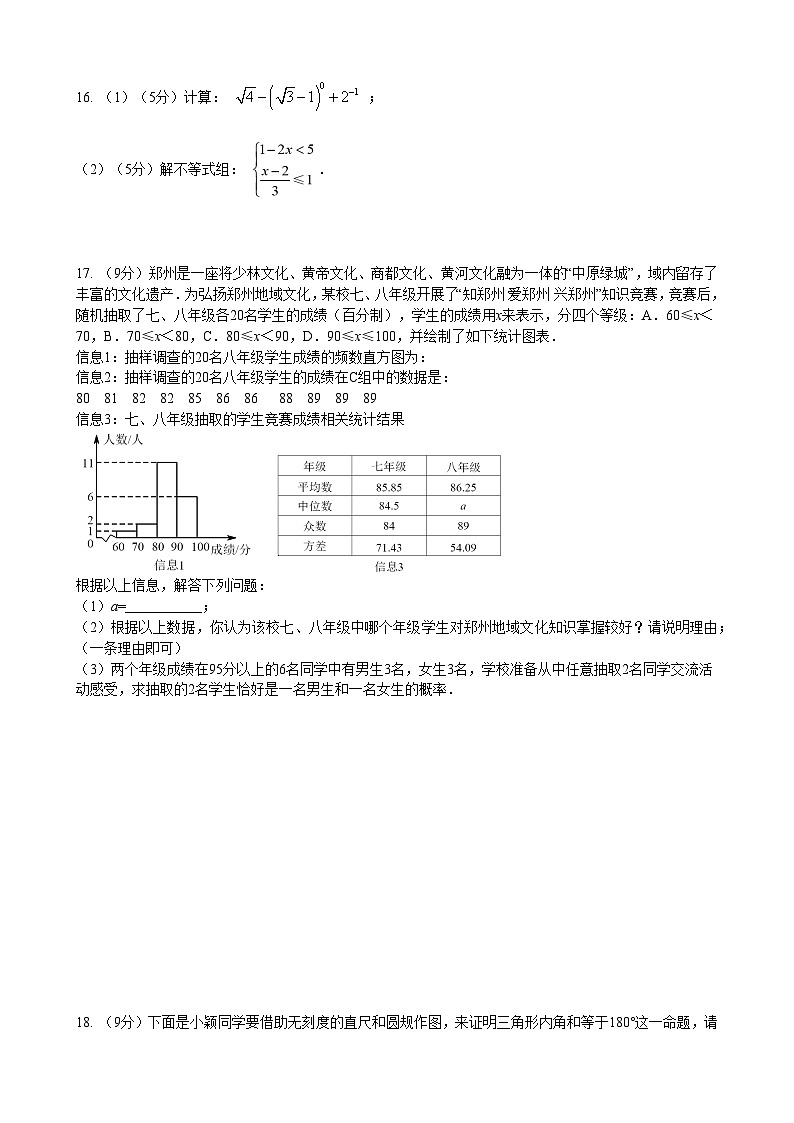
17. (9分)郑州是一座将少林文化、黄帝文化、商都文化、黄河文化融为一体的“中原绿城”,域内留存了丰富的文化遗产.为弘扬郑州地域文化,某校七、八年级开展了“知郑州 爱郑州 兴郑州”知识竞赛,竞赛后,随机抽取了七、八年级各20名学生的成绩(百分制),学生的成绩用x来表示,分四个等级:A.60≤x<70,B.70≤x<80,C.80≤x<90,D.90≤x≤100,并绘制了如下统计图表.
信息1:抽样调查的20名八年级学生成绩的频数直方图为:
信息2:抽样调查的20名八年级学生的成绩在C组中的数据是:
80 81 82 82 85 86 86 88 89 89 89
信息3:七、八年级抽取的学生竞赛成绩相关统计结果
根据以上信息,解答下列问题:
(1)a=___________;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生对郑州地域文化知识掌握较好?请说明理由;(一条理由即可)
(3)两个年级成绩在95分以上的6名同学中有男生3名,女生3名,学校准备从中任意抽取2名同学交流活动感受,求抽取的2名学生恰好是一名男生和一名女生的概率.
18. (9分)下面是小颖同学要借助无刻度的直尺和圆规作图,来证明三角形内角和等于180°这一命题,请你帮她补充完整.
19. (9分)“九年磨一剑,六月试锋芒”,为助力中考,有效缓解学生的考前压力,某中学九年级学生开展了考前减压团体拓展活动.学校准备了“能量传输”类与“鱼跃龙门”类共15个小项目,其中“能量传输”类项目比“鱼跃龙门”类项目数的2倍少3个.
(1)“能量传输”类项目和“鱼跃龙门”类项目各有多少个?
(2)“能量传输”和“鱼跃龙门”两类项目的平均用时分别是6分钟、8分钟(项目转场时间忽略不计),由于时间的限制,在实际拓展活动时,两种类型的项目只能开展10个,且“鱼跃龙门”类项目数多于“能量传输”类项目数的一半,活动应该怎么设计能使得所用的时间最少?
20. (9分)生命在于运动.体育运动伴随着我们每一天,科学的体育运动不仅能强健体魄,更能愉悦身心.但与此同时我们也可以看到,因为不遵循运动规律而导致身体损伤的事情时有发生,我们越来越重视科学运动.衡量科学运动的重要指标之一就是心率.研究发现,运动过程中影响心率的主要因素有年龄、性别、运动强度、运动时间、运动类型、运动项目、情绪等.数学兴趣小组在分析了以上因素后,用统计和函数的知识,深入研究了在慢跑和跳绳过程中,心率与时间的关系如下表:
计算机将慢跑时的平均心率与跳绳时的平均心率与时间的关系拟合成一次函数的图象如图1:
计算机将慢跑时的平均心率与时间的关系拟合成的另一种函数的图象如图2:
(1)根据图1中的信息,你发现在哪项运动中心率随时间的变化更快?请说明理由;
(2)甲同学慢跑运动后的心率为158次/分,根据图1中的信息请你估算甲同学运动的时间;
(3)有同学认为,计算机将慢跑时的平均心率与时间的关系拟合成的一次函数关系与实际的测量结果误差比较大,所以又借助计算机将其拟合为另一种函数关系,如图2,请你根据实际情况说明他的分析是否合理?并说明理由.
21. (9分)如图,在Rt△ABC中,∠A=90°,点D在斜边BC上,直角边AC恰好与以BD为直径的半圆相切于点E,连接DE,过点O作OF∥DE,交AB 于点F.
(1)请判断四边形BOEF的形状,并说明理由;
(2)若AE=6,sin∠C=,求AB的长.
22. (10分)如图,正方形ABCD,AB=4,动点E从点A出发沿AD向点D运动,连接BE,以BE为边在其右侧作正方形BEFG,EF与CD相交于点H.
(1)在点E的运动过程中,点G的位置也随之改变,则点G始终在直线DC上吗?如果在,请给出证明,如果不在,请说明理由;
(2)当点E在AD边上运动时,△BHG的面积如何变化?请写出研究过程.
23. (10分)如图,抛物线y=-x2+bx+c与x轴,y轴分别交于A,B两点,点B坐标为(0,5),抛物线的顶点为C,点B关于对称轴直线x=2的对称点为点D.
(1)求该抛物线的表达式;
(2)当-1<x<4时,求函数值y的取值范围;
(3)将抛物线在点D下方的图象沿着直线BD向上翻折,抛物线的其余部分保持不变,得到一个新图象,当直线y=x+n与新图象有2个公共点时,请直接写出n的值.
2023年中招第二次适应性测试
数学 评分参考
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.C 2.D 3.B 4.D 5.C 6.C 7.A 8.B 9.A 10.A
二、填空题(每小题3分,共15分)
11.(答案不唯一,写出一个即可)12.x=1;13. 75;14.;15.
三、解答题(本大题共8个小题,满分75分)
16.(1)解:原式=…………………………………………………………3分
=………………………………………………………………5分
(2)
由①得, ……………………………………………………………2分
由②得, …………………………………………………………4分
∴ 不等式组的解集为……………………………………………………………5分
17.解(1)87.……………………………………………………………………………………3分
(2)我认为八年级学生对郑州地域文化知识掌握较好.因为八年级学生竞赛成绩的平均数比七年级的高,而且方差比七年级的小.(答案不唯一,只要合理即可)……………6分
(3)将3名男生分别记为男1,男2,男3,3名女生分别记为女1,女2,女3,然后列表如下:
男1
男2
男3
女1
女2
女3
男1
(男2,男1)
(男3,男1)
(女1,男1)
(女2,男1)
(女3,男1)
男2
(男1,男2)
(男3,男2)
(女1,男2)
(女2,男2)
(女3,男2)
男3
(男1,男3)
(男2,男3)
(女1,男3)
(女2,男3)
(女3,男3)
女1
(男1,女1)
(男2,女1)
(男3,女1)
(女2,女1)
(女3,女1)
女2
(男1,女2)
(男2,女2)
(男3,女2)
(女1,女2)
(女3,女2)
女3
(男1,女3)
(男2,女3)
(男3,女3)
(女1,女3)
(女2,女3)
总共有30种等可能的结果,而恰好是一名男生和一名女生的结果数有18种,所以,一名男生一名女生的概率为.…………………………………………………………9分
18.证明:如图,………………………………………………………………………4分
∵∠DAE=∠B,
∴AE//BC.
∴∠EAC=∠C.
∵∠BAC+∠EAC+∠DAE=180°,
∴∠BAC+∠C+∠B=180°.
即三角形三个内角的和等于180°………………………9分
(注:若尺规作图不正确,但证明正确,给5分.)
19.解(1)设“能量传输”类项目x个,“鱼跃龙门”类项目y个,
由题意可得: ....………......................................………...……….....………3分
解得
答:“能量传输”类项目9个,“鱼跃龙门”类项目6个...................…..….....………5分
(2)设实际拓展活动所用时间为y,开展了a个“能量传输”类项目,则“鱼跃龙门”类项目()个.
由题意得:
,即………..........................................................……......…….....……6分
即………...........................……....……….....……7分
∵﹣2<0,∴y随着a的增大而减小.
∵a为正整数,∴当a=6时,y值最小.
即当实际拓展活动中,开展6个“能量传输”类项目,4个“鱼跃龙门”类项目,能使所用的时间最少........................……….....…………….....…...…….....……...................……9分
20.解:(1)跳绳这项运动中心率随时间的变化更快,理由不唯一,可以从表格或k的值等方面说明.……….......................................................……......……..........……......…….....……3分
(2)当y1=158时,158=0.35x+109,
解得x=140.
即甲同学运动的时间大约为140秒..........................……......……..........…….....……6分
(3)随着慢跑运动时间的增加,心率不会一直增加,也不会出现明显的下降,但心率增加的速度会减慢,所以用图2中函数拟合更合理(理由充分即可)........................……9分
21.解:(1)四边形BOEF是菱形,理由如下:.....................……....…..........…….....……1分
∵与AC相切,∴∠OEC=90°.
∵∠A=90°,∴OE//AB.∴∠BFO=∠FOE.
∵OF∥DE,∴∠BOF=∠ODE,∠FOE=∠OED.
∵OD=OE,∴∠ODE=∠OED.∴∠BFO=∠BOF.
∴BF=BO.....................……......................…..................…...................……..........…….....……3分
∴BF=OE.
∵BF//OE,∴四边形BOEF是平行四边形............................……..........…….....……4分
∵BF=BO,
∴四边形BOEF是菱形...............…..................…...................…….........…..........…….....……5分
(2)∵四边形BOEF是菱形,∴EF//BC.
∴∠C=∠FEA.∴在Rt△AEF中sin∠AEF=
即cos∠AEF==
∴EF=10.∴AF=8,BF=10.
∴AB=18....................................................................................................................................9分
22.(1)如图,连接CG,
∵四边形ABCD和四边形BEFG为正方形,∴∠ABC=∠EBG=90°,AB=AC,BE=BG.
∴∠ABC﹣∠EBC=∠EBG﹣∠EBC.即∠ABE=∠CBG.
∴△ABE≌CBG(SAS).
∴∠BCG=∠A=90°.
∵∠BCD=90°,∴∠BCD+∠BCG=180°.
即D,C,G三点共线,
∴点G始终在直线DC上················································································5分
(2)设AE=x,
∵△ABE∽△DEH,∴
∴∴
∴
由(1)可知,CG=AE,∴
∴
∵x>0且当点E从点A运动到点D时,x在逐渐增大,
∴S△BHG的面积随x的增大而增大.
即当点E从点A运动到点D时,S△BHG的面积逐渐增大.········································10分
23.解:(1)将B(0,5)代入y= -x2+bx+c中得c=5,
∵对称轴x==2,即,∴b=4.
∴抛物线的表达式为y= -x2+4x+5.....……….....………......................................…….....……3分
(2)当x=-1时,y=-1-4+5=0;当x=4时,y=5;当x=2时,y=-4+8+5=9,
∴当-1<x<4时,y的取值范围为0<y≤9…….....………..........................……….....……6分
(3)①当直线y=x+n过点D时:
∵B,D两点关于对称轴直线x=2对称,B(0,5),
∴点D的坐标为(4,5).
将点D(4,5)代入直线y=x+n中得5=4+n,
∴n=1.
②当直线y=x+n与抛物线y= -x2+4x+5相切时,
令x+n= -x2+4x+5,即 -x2+3x+5-n=0.
当解得
综上:n=1或..………..............................................................................…….....……10分
2023年河南郑州市中考第二次适应性测试数学试题及答案: 这是一份2023年河南郑州市中考第二次适应性测试数学试题及答案,共11页。
郑州市2023年中招第一次适应性测试数学试卷(pdf版含答案): 这是一份郑州市2023年中招第一次适应性测试数学试卷(pdf版含答案),共10页。
2023年河南省郑州市中考第一次适应性测试数学试题: 这是一份2023年河南省郑州市中考第一次适应性测试数学试题,共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













