各版本通用 中考第二轮复习题型专题训练（一）

这是一份各版本通用 中考第二轮复习题型专题训练（一），共16页。试卷主要包含了一次函数旋转题型，反比例函数中一次函数旋转题型等内容，欢迎下载使用。
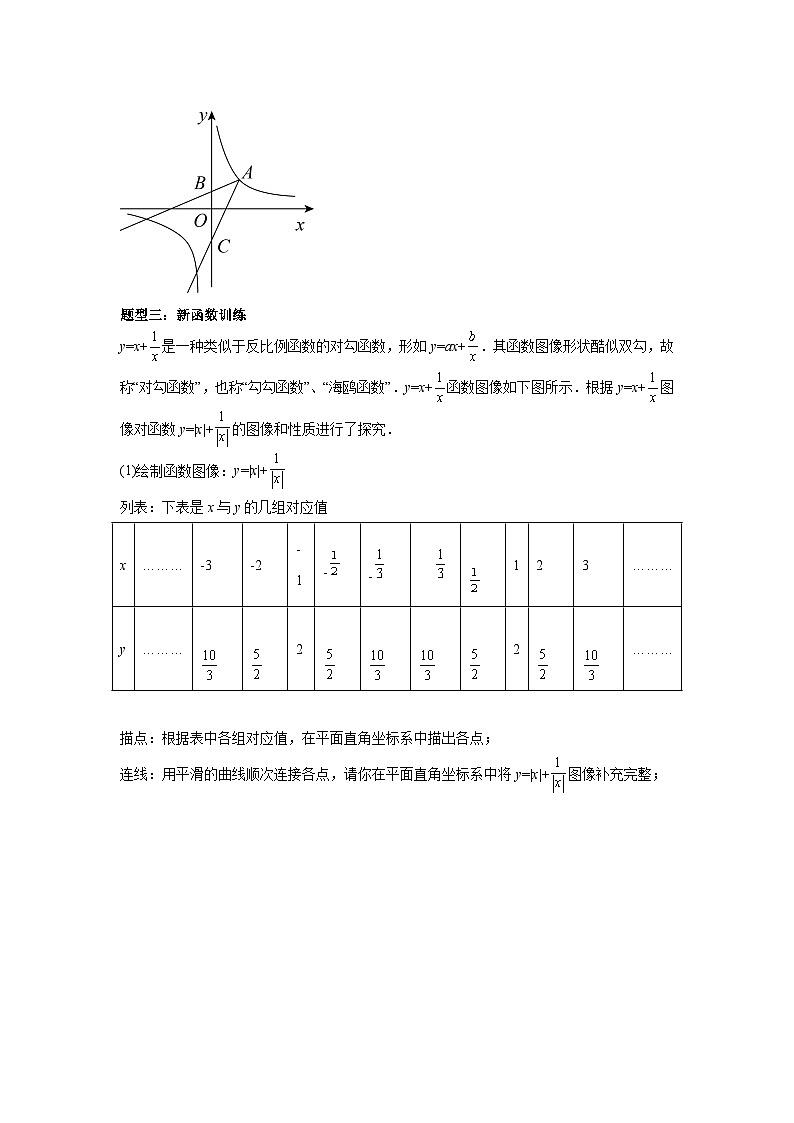
中考第二轮复习题型专题训练（一）题型一、一次函数旋转题型 1.如图一次函数的图象与x轴、y轴分别交于点A、B，把直线绕点B顺时针旋转交x轴于点C．则线段的长为______．2.如图，在平面直角坐标系中，直线y=x+6与x轴，y轴分别交于点D，点E，点F为直线y=x+6上一点，横坐标为-4．把直线DE绕F点顺时针旋转，与x轴负半轴，y轴正半轴分别交于点A，点C，若S△ADF=S△FEC，则直线AC的解析式为______．3.已知一次函数y＝x＋1的图像与y轴交于点A，将该函数图像绕点A旋转45°，旋转后的图像对应的函数关系式是_____． 题型二、反比例函数中一次函数旋转题型 如图，已知点A的横坐标与纵坐标相等，点B（0，2），点A在反比例函数y的图象上．作射线AB，再将射线AB绕点A按逆时针方向旋转，交y轴于C点，则△ABC面积为_____．题型三：新函数训练y=x+是一种类似于反比例函数的对勾函数，形如y=ax+．其函数图像形状酷似双勾，故称“对勾函数”，也称“勾勾函数”、“海鸥函数”．y=x+函数图像如下图所示．根据y=x+图像对函数y=|x|+的图像和性质进行了探究．(1)绘制函数图像：y=|x|+列表：下表是x与y的几组对应值x………-3-2-1--        123………y………        2                2        ……… 描点：根据表中各组对应值，在平面直角坐标系中描出各点；连线：用平滑的曲线顺次连接各点，请你在平面直角坐标系中将y=|x|+图像补充完整；(2)观察发现：①写出函数y=|x|+的一条性质_________②函数图像与直线y=2有_________个交点，所以对应的方程|x|+有_________个实数根．(3)分析思考：③方程的|x-1|+-2=0的解为_________④不等式|x|+-＜0，x的取值范围为_________(4)延伸探究：⑤当x＞0时，直线y=kx+3与y=|x|+只有一个交点，求k的值？          题型四：多学科融合题型杠杆原理在生活中被广泛应用（杠杆原理：阻力×阻力臂=动力×动力臂），小明利用这一原理制作了一个称量物体质量的简易“秤”（如图1）．制作方法如下：第一步：在一根匀质细木杆上标上均匀的刻度（单位长度1cm），确定支点，并用细麻绳固定，在支点左侧2cm的A处固定一个金属吊钩，作为秤钩；第二步：取一个质量为0.5kg的金属物体作为秤砣．(1)图1中，把重物挂在秤钩上，秤砣挂在支点О右侧的B处，秤杆平衡，就能称得重物的质量．当重物的质量变化时，的长度随之变化．设重物的质量为，的长为．写出y关于x的函数解析式；若，求的取值范围．(2)调换秤砣与重物的位置，把秤砣挂在秤钩上，重物挂在支点О右侧的B处，使秤杆平衡，如图2．设重物的质量为，的长为，写出y关于x的函数解析式，完成下表，画出该函数的图象．……0.250.5124…………     ……           题型五：新定义阅读理解题阅读下列材料定义运算：，当时，；当时，．例如：；．完成下列任务 (1)① _________；②_________(2)如图，已知反比例函数和一次函数的图像交于、两点．当时，．求这两个函数的解析式．          中考第二轮复习题型专题训练（一）（解析）题型一、一次函数旋转题型 1.如图一次函数的图象与x轴、y轴分别交于点A、B，把直线绕点B顺时针旋转交x轴于点C．则线段的长为______．【答案】##【分析】根据一次函数表达式求出点A和点B坐标，得到为等腰直角三角形和的长，过点C作，垂足为D，证明为等腰直角三角形，设，结合旋转的度数，用两种方法表示出，得到关于x的方程，解之即可．【详解】解：一次函数的图象与x轴、y轴分别交于点A，B，令，则；令，则，则，，则为等腰直角三角形，，，过点C作，垂足为D，，为等腰直角三角形，设，，由旋转的性质可知，，，，，解得：，．故答案为：．【点睛】本题主要考查了一次函数与坐标轴的交点问题，等腰直角三角形的判定和性质，直角三角形的性质，勾股定理，二次根式的混合运算，知识点较多，解题的关键是作出辅助线，构造特殊三角形．2.如图，在平面直角坐标系中，直线y=x+6与x轴，y轴分别交于点D，点E，点F为直线y=x+6上一点，横坐标为-4．把直线DE绕F点顺时针旋转，与x轴负半轴，y轴正半轴分别交于点A，点C，若S△ADF=S△FEC，则直线AC的解析式为______．【答案】y=x+3【分析】由S△ADF=S△FEC，推出S△ADF+ S四边形CODF =S△FEC+ S四边形CODF，即S△AOC=S△EOD，设直线AC的解析式为y=kx+b，根据题意得出b2-9b+18=0，继续计算即可求解．【详解】解：令x=0，则y=6，令y=0，则x=-6，∴点D(-6，0)，点E(0，6)，∴OD=OE=6，∵点F为直线y=x+6上一点，横坐标为-4，∴y=-4+6=2，∴点F(-4，2)，∵S△ADF=S△FEC，∴S△ADF+ S四边形CODF =S△FEC+ S四边形CODF，∴S△AOC=S△EOD，设直线AC的解析式为y=kx+b，　则点A(-，0)，点E(0，b)，∴OA=，OC=b，根据题意得：，，整理得：b2-9b+18=0，解得：b=6(舍去)或b=3，当b=3时，k=，∴直线AC的解析式为y=x+3，故答案为：y=x+3．【点睛】本题考查了一次函数图象上点的坐标特征、三角形的面积，解题的关键是利用三角形的面积公式结合S△ADF=S△FEC，找出关于b的一元二次方程．3.已知一次函数y＝x＋1的图像与y轴交于点A，将该函数图像绕点A旋转45°，旋转后的图像对应的函数关系式是_____．【答案】y＝－x＋1 或y＝3x＋1【分析】分两种情况讨论，通过三角形全等，求得D的坐标，然后根据待定系数法即可求得旋转后的图象对应的函数关系式．【详解】解：如图1，∵一次函数y=x+1的图象与y轴交于点A，与x轴交于B，∴A（0，1），B（-2，0），   当直线y=x+1绕点A顺时针旋转45°后的图象为直线l，过B作BD⊥直线l于D，过D作FD⊥y轴于F，过B作BE⊥FD延长线于E，则△ABD为等腰直角三角形，∵∠EDB+∠FDA=∠EDB+∠EBD=90°，BD=AD，∴∠FDA=∠EBD，∴△ADF≌△DBE（AAS），设AF=a，则DE=a，∵点A（0，1），点B（-2，0），∴DF=BE=OF=1+a，EF=ED+DF=a+1+a=OB=2，∴a=，∴DF=OF=1+a=，∴D（-，），设直线l的解析式为y=kx+1，则=-k+1，解得k=-，∴y=-x+1；如图2，直线y=x+1绕点A逆时针旋转45°后的图象为直线l，过B作BD⊥直线l于D，过D作FD⊥y轴于F，作DE⊥x轴于E，则△ABD为等腰直角三角形，同理可得△ADF≌△BDE（AAS），设DF=b，则DE=b，∵点A（0，1），点B（-2，0），∴AF=BE=1+b，BO=BE+OE=b+1+b=OB=2，∴b=，∴D（-，-），设直线l的解析式为y=kx+1，则-=-k+1，解得k=3，∴y=3x+1；综上，旋转后的图象对应的函数关系式是y=-x+1或y=3x+1．故答案为y=-x+1或y=3x+1．【点睛】本题考查了一次函数图象与几何变换，旋转的性质以及一次函数图象上点的坐标特征的运用，解决问题的关键是利用45°角，作辅助线构造等腰直角三角形． 题型二、反比例函数中一次函数旋转题型 如图，已知点A的横坐标与纵坐标相等，点B（0，2），点A在反比例函数y的图象上．作射线AB，再将射线AB绕点A按逆时针方向旋转，交y轴于C点，则△ABC面积为_____．【答案】20【分析】过B作BF⊥AC于F，过F作FD⊥y轴于D，过A作AE⊥DF延长线于E，证明△AEF≌△FDB（AAS），设BD＝a，则EF＝a，由点A（4，4）和点B（0，2）可得AE+OD＝4，求得，可得F（3，1），进而求得直线AC的解析式为y＝3x﹣8，令x＝0，得出C（0，﹣8），即可求解．【详解】解：∵点A在反比例函数y的图象上，且点A的横坐标与纵坐标相等，∴A（4，4），过B作BF⊥AC于F，过F作FD⊥y轴于D，过A作AE⊥DF延长线于E，∵，则△ABF为等腰直角三角形，∴在△AEF与△FDB中∴△AEF≌△FDB（AAS），设BD＝a，则EF＝a，∵点A（4，4）和点B（0，2），∴DF＝4﹣a＝AE，OD＝OB﹣BD＝2﹣a，∵AE+OD＝4，∴4﹣a+2﹣a＝4，解得a＝1，∴F（3，1），设直线AC的解析式为y＝kx+b，则，解得，∴y＝3x﹣8，令x＝0，则y＝﹣8，∴C（0，﹣8），∴BC＝10，∴20，故答案为：20．【点睛】本题考查了反比例函数与一次函数综合，坐标与图形，全等三角形的性质与判定，等腰直角三角形的性质，一次函数与几何图形，数形结合是解题的关键．题型三：新函数训练y=x+是一种类似于反比例函数的对勾函数，形如y=ax+．其函数图像形状酷似双勾，故称“对勾函数”，也称“勾勾函数”、“海鸥函数”．y=x+函数图像如下图所示．根据y=x+图像对函数y=|x|+的图像和性质进行了探究．(1)绘制函数图像：y=|x|+列表：下表是x与y的几组对应值x………-3-2-1--        123………y………        2                2        ……… 描点：根据表中各组对应值，在平面直角坐标系中描出各点；连线：用平滑的曲线顺次连接各点，请你在平面直角坐标系中将y=|x|+图像补充完整；(2)观察发现：①写出函数y=|x|+的一条性质_________②函数图像与直线y=2有_________个交点，所以对应的方程|x|+有_________个实数根．(3)分析思考：③方程的|x-1|+-2=0的解为_________④不等式|x|+-＜0，x的取值范围为_________(4)延伸探究：⑤当x＞0时，直线y=kx+3与y=|x|+只有一个交点，求k的值？【答案】(1)见解析(2)①关于y轴对称；②2；2(3)③x1=2，x2=0；④或(4)或1【分析】（1）先描点，再连线即可得到；（2）①通过观察图像，可得图像关于轴对称；②利用数形结合的思想进行求解，把方程的解转化为图像之间的交点的横坐标即可求解；（3）③根据图像的平移的性质即可求解；④通过数形结合的思想进行求解即可；（4）把交点转化为方程的根，一个交点，即方程只有一个根，需要进行分类讨论．【详解】（1）解：y=|x|+图像如下：    （2）解：①通过观察图像可得：y=|x|+图像关于轴对称，故答案为：关于y轴对称；②如图可知函数图像与直线y=2有2个交点；即方程|x|+有2个实数根；故答案为：2，2；（3）解：③方程的|x-1|+-2=0的解为方程|x|+的解x1=1，x2=-1向右平移一个单位，得x1=2，x2=0，④当|x|+-，由图像可得解为：，不等式|x|+-＜0的解集为：或；故答案为：x1=2，x2=0；或；（4）解：当x＞0时，直线y=kx+3与y=|x|+只有一个交点，即只有一个根，，      ，当时，解得；当时，是一元二次方程，，即，解得：，综上：k的值为或1时，直线y=kx+3与y=|x|+只有一个交点．【点睛】题考查了反比例函数的图像和性质、画函数图象、方程的根、不等式的解集、函数图象的平移，解题的关键是理解题意，运用数形结合的思想进行求解．题型四：多学科融合题型杠杆原理在生活中被广泛应用（杠杆原理：阻力×阻力臂=动力×动力臂），小明利用这一原理制作了一个称量物体质量的简易“秤”（如图1）．制作方法如下：第一步：在一根匀质细木杆上标上均匀的刻度（单位长度1cm），确定支点，并用细麻绳固定，在支点左侧2cm的A处固定一个金属吊钩，作为秤钩；第二步：取一个质量为0.5kg的金属物体作为秤砣．(1)图1中，把重物挂在秤钩上，秤砣挂在支点О右侧的B处，秤杆平衡，就能称得重物的质量．当重物的质量变化时，的长度随之变化．设重物的质量为，的长为．写出y关于x的函数解析式；若，求的取值范围．(2)调换秤砣与重物的位置，把秤砣挂在秤钩上，重物挂在支点О右侧的B处，使秤杆平衡，如图2．设重物的质量为，的长为，写出y关于x的函数解析式，完成下表，画出该函数的图象．……0.250.5124…………     ……【答案】(1)；   (2)，表、图见解析【分析】（1）根据阻力×阻力臂=动力×动力臂解答即可；（2）根据阻力×阻力臂=动力×动力臂求出解析式，然后根据列表、描点、连线的步骤解答．(1)解：∵阻力×阻力臂=动力×动力臂，∴重物×OA=秤砣×OB．∵OA=2cm，重物的质量为，的长为，秤砣为0.5kg，∴2x=0.5y，∴；∵4>0，∴y随x的增大而增大，∵当y=0时，x=0；当y=48时，x=12，∴．(2)解：∵阻力×阻力臂=动力×动力臂，∴秤砣×OA=重物×OB．∵OA=2cm，重物的质量为，的长为，秤砣为0.5kg，∴2×0.5=xy，∴；当x=0.25时，；当x=0.5时，；当x=1时，；当x=2时，；当x=4时，；填表如下：……0.250.5124…………421……画图如下：【点睛】本题考查了一次函数的应用，反比例函数的应用，以及列表、描点、连线画函数图象的方法，求出函数解析式是解答本题的关键．题型五：新定义阅读理解题阅读下列材料定义运算：，当时，；当时，．例如：；．完成下列任务 (1)① _________；②_________(2)如图，已知反比例函数和一次函数的图像交于、两点．当时，．求这两个函数的解析式．【答案】(1)①1；②   (2)，【分析】（1）根据材料中的定义进行计算，即可求出答案；（2）由函数图像可知当时，，则，结合已知可得，即可求出b，得到一次函数解析式，求出点A的坐标，再利用待定系数法求出反比例函数解析式．(1)解：根据题意，∵，当时，；当时，，∴①；∵，∴②；故答案为：①1；②；(2)解：由函数图像可知当时，，∴，又∵，∴，∴，∴一次函数，当x＝－2时，，∴A（－2，1），将A（－2，1）代入得，∴反比例函数．【点睛】本题考查了新定义的运算法则，零次幂，反比例函数与一次函数的综合问题，解题的关键是掌握题意，正确的运用数形结合的思想求解．