2023年中考数学二轮复习必会几何模型剖析--3.2 “手拉手”模型（旋转）（全等模型）（精品课件）

这是一份2023年中考数学二轮复习必会几何模型剖析--3.2 “手拉手”模型（旋转）（全等模型）（精品课件），共28页。PPT课件主要包含了连接AG，分析转化比例，求出AB即可，∴PC平分∠BPD，∴CGCH，∴BEDG，∴∠CBE∠CDG，由勾股定理得，∵ABAC，∴CDBP5等内容，欢迎下载使用。

手拉手模型---常见题型
手拉手模型---正多边形
手拉手模型---构造模型
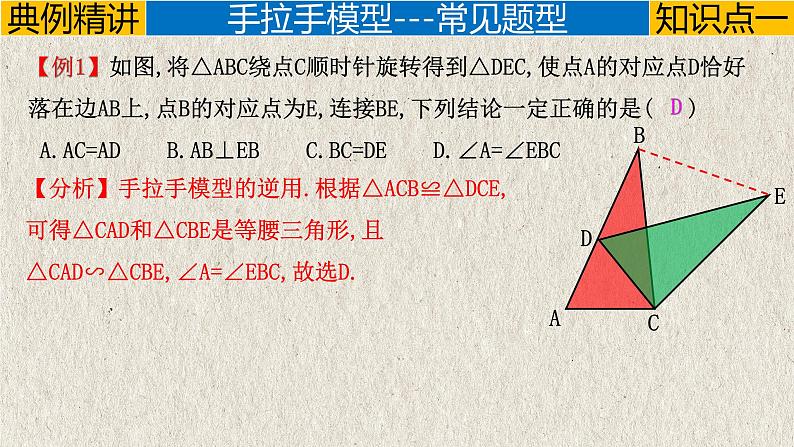
【例1】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( ) A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
【分析】手拉手模型的逆用.根据△ACB≌△DCE,可得△CAD和△CBE是等腰三角形,且△CAD∽△CBE,∠A=∠EBC,故选D.
【条件】如图,OA=OB,OC=OD,有时候会直接以特殊几何图形的形式给出,比如我们都很熟悉的等边三角形和正方形.
【结论】△OAC≌△OBD(SAS)如图,OA=OB,OC=OD(四线共点),∠AOB=∠COD(夹角相等)
【特征】四点共线,两两相等,夹角相等.
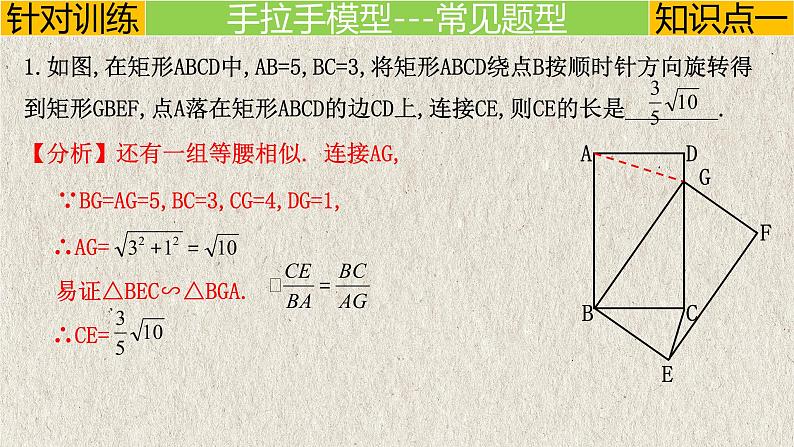
1.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是________.
【分析】还有一组等腰相似.
易证△BEC∽△BGA.
∵BG=AG=5,BC=3,CG=4,DG=1,
【小结】以上例子解题关键皆在于利用那一组等腰三角形相似,有些问题常有变式，因其条件与结论可以互换.
连接AC、AC´、AG,
易证△ABB´∽△ACC´,
连接设AB´=x,则B´G=x,DG=x-4,
AG2=AB´2+B´G2=AD2＋DG2，
代入得:x²+x²=72+(x-4)²,
解得:x=5,x=-13(舍去),
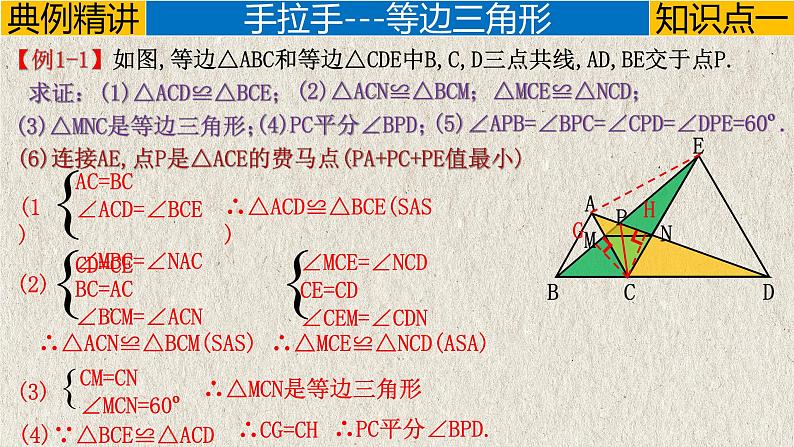
【例1-1】如图,等边△ABC和等边△CDE中B,C,D三点共线,AD,BE交于点P.
求证：(1)△ACD≌△BCE；
∴△ACD≌△BCE(SAS)
(2)△ACN≌△BCM；△MCE≌△NCD；
∴△ACN≌△BCM(SAS)
∴△MCE≌△NCD(ASA)
(3)△MNC是等边三角形；
∴△MCN是等边三角形
(4)PC平分∠BPD；
(4)∵△BCE≌△ACD
(5)∠APB=∠BPC=∠CPD=∠DPE=60º.
(6)连接AE,点P是△ACE的费马点(PA+PC+PE值最小)
【例1-2】如图,正方形ABCD和正方形CEFG边长分别为a和b,BE,DG交于点H.
求证：(1)△BCE≌△DCG；
∴△BCE≌△DCG(SAS)
(2)BE=DG,BE⊥DG；
(2)∵△BCE≌△DCG
∴∠DHB=∠BCD-90(旋转角都相等)
(3)DE2+BG2=2a2+2b2；
(3)连接BD、EG,
∴DE2+BG2=BD2+EG2,
BD2=BH2+DH2,EG2=EH2+GH2,DE2=DH2+EH2,BG2=BH2+GH2,
∴DE2+BG2=2a2+2b2.
【重点概述】手拉手模型是一种基本的旋转型全等,与其说看图找模型，不如是“找条件、定模型”.
从前面,我们已经知道“手拉手”模型,有时题目中“手拉手”模型不明显,常常要作辅助线构造“手拉手”模型.【情形1】当题目出现一对相似三角形时,一般我们考虑是否可用“手拉手”模型求解,若“拉手”线没有连,先补连“拉手”线；
【情形2】当题目没有出现有一个公共顶点的相似三角形时,我们就需要通过“补形”来构造一对有一个公共顶点的相似三角形,从而构造“手拉手”模型进行求解；如图①②,已知等腰Rt△PAC和一条“拉手”线AB,我们考虑以P为顶点,PB为边作等腰Rt△PBD,再连接另一条拉手线CD,则可得到△PBD∽△PAC,△ABP≌△CDP.
1.如图①,在▱ABCD中,AC=BC,∠ACB=90º,将△ACB绕点A逆时针旋转,旋转角为α,且0º≤α≤90º,请在图②,③中分别画出当△ABD为直角三角形时的两种情形．
当∠BAD=90º时,作图如解图②；
当∠ADB=90º时,作图如解图③.
2.如图①,在Rt△ABC中,∠BAC＝90º,AB＝AC,D、E两点分别在AC、BC上,且DE∥AB,CE＞AC.将△CDE绕点C按顺时针方向旋转,请在图②,③中作出当△CDE旋转至A、B、E三点共线时的两种情形．
当点E在线段AB上时，作图如解图②；
当点E在BA的延长线上时，作图如解图③.
3.如图①,在△ABC和△ADE中,∠BAC=∠DAE=90º,AD=AE,AB=AC,点P为射线BD,CE的交点,若把△ADE绕点A旋转,请在图②,③中作出当AD∥CP时的两种情形．
若AD∥PC,则∠AEC=∠DAE=90º.当点E在直线AC左侧,且∠AEC=90º时,作图如解图①；
当点E在直线AC右侧,且∠AEC=90º时,作图如解图②.
4.如图①,在等边△ABC中,CD是边AB上的高,点P是直线CD上一点,连接AP,将AP绕点P逆时针旋转60º得到PE,连接CE,请在图②,③中作出当∠CEB=30º时的两种情形.
根据题意可得∠CBE=90º.若∠CEB=30º,当点E在CA的延长线上,且EA=AB时,作图如解图①；
当CE∥AB时,作图如解图②；
作图形如解图,当△ADE旋转180º时,此时ED与BC平行,△MPN的面积最大.
6.如图①,在Rt△ABC和Rt△BDF中,∠ABC=∠FBD=90º,AB=BC,BF=BD,且AB=2BD,点E为线段AB的中点,连接AD,M是AD的中点,连接BM.把△BDF绕点B在平面内自由旋转,请在图②,③中,作出CM的长为最大值和最小值的图形.
如解图①,当点M落在线段CE上时,CM的长度最小；
如解图②,当点M落在线段CE的延长线上时,CM的长度最大.
【例3】已知△ABC.(1)如图①,∠BAC=90º,∠ACB=30º,D、E是AB、AC的中点,如图②,将△ADE绕点A逆时针旋转,连接BD、CE.则CE:BD=____；(2)如图③,∠BAC=90º,BA=AC,D是BC边上一点,连接AD,将AD绕点A逆时针旋转90º,得到AE,连接DE,F是DE的中点,连接CF,则CF:AD=____；(3)如图④,AB=AC,∠BAC=60º,点P在△ABC内,且∠APC=150º,PA=3,PC=4.以AP为边向右侧作等边△APD,则PB的长为____；
(4)如图⑤,点P在等边△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数；
(4)如图⑤,以AP为边,在AP的左上方作等边△APD,连接DC,
则DP=AD=AP=3,∠APD=∠DAP=60º=∠BAC,
在△DPC中,DP2+CP2=32+42=52=CD2，
∴∠BAP=∠CAD，
∴△APB≌△ADC，
∴∠APC=∠DPC-∠DPA=90º-60º=30º；
(5)在Rt△ABC中,AB=2AC,
∵∠BAC=∠PAD=60º,
∴∠APD=∠ABC=30º.∠ADP=∠ACB=90º.
∴△APD∽△ABC，
∴△ABP∽△ACD，
∴∠ABC=30º,∠BAC=60º.
将AP绕点A逆时针旋转60º,得到AE,
在AE上截取AD=0.5AP,连接DP,DC.
∴△DAB≌△PAC(SAS),
解:∵∠ACB=60º,∠APD=60º,AC=BC,AP=PD,
∴△ACB与△APD都是等边三角形，
∴AC=AB,AP=AD,∠CAB=∠PAD,
∴∠CAB-∠PAB=∠PAD-∠PAB,即∠PAC=∠DAB,
∴直线BD与直线CP相交所成的较小角的度数为60º.
∵△APC≌△ADB,
∴∠ACP=∠ABD,
设CP与BD的延长线交于点E,如解图1,
∴∠CEB=180º-∠PCB-∠CBD=180º-(60º-∠ACP)-(60º+∠ABD)=60º,
∴∠CAB+∠DAC=∠PAD+∠DAC.即∠DAB=∠PAC.
∵∠BHA=∠CHG,
理由:∵∠ACB=90º,CA=CB，
∴∠CAB=45º,
∴△DAB∽△PAC.
设BD交CP于点G,交CA于点H.如解图2,
∴∠CGH=∠BAH=45º；
(3)【解决问题】当α=90º时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时AD:CP的值．
1)如图3,由EF∥AB得,∠CEP=∠CAB=45º.
在Rt△APC中,点E为AC中点.
由题可知,∠CPA=∠QPA=90º.
∴PE=0.5AC=AE=CE.
∴∠ECP=∠EPC=67.5º,∠EAP=∠EPA=22.5º.
∴∠DAC=67.5º=∠ECP.
∴∠ECD=∠EAD=22.5º,
2)如图4,设AP=DP=b,
在Rt△CPA中,E为AC的中点,
∴PE=0.5AC=AE=EC,
∴∠PAE=67.5º,
解：∵四边形ABCD是正方形.
∴△DEB´是等腰直角三角形；
∴∠BAD=90º,AB=AD.
由旋转性质得AB=AB´,∠BAB´=60º,
∴△ABB´是等边三角形，
∴∠AB´B=60º,∠B´AD=30º,AD=AB´,
∴∠AB´D=(180º-30º)÷2=75º,
∴∠EB´D=180º-60º-75º=45º.
∴∠EDB´=∠EB´D=45º.
∵△DEB´是等腰直角三角形,四边形ABCD是正方形,
∵∠EDB´=∠BDC，
∴∠B´DB=∠EDC，
∴△B´DB∽△EDC，
(2)当0º＜α＜360º,且α≠90º时,①(1)中的两个结论是否仍然成立?如果成立.请仅就图2的情形进行证明；如果不成立.请说明理由；
证明：如图,连接BD.
∴∠AB´D=135º-0.5α/2,
∵AB=AB´,∠BAB´=α,
∴∠AB´B=90º-0.5α/2，
∵∠B´AD=α-90º,AD=AB´,
∴∠EB´D=∠AB´D-∠AB´B=45º.
∴△DEB´是等腰直角三角形,
∵四边形ABCD为正方形.
要使点B´,E,C,D为顶点的四边形为平行四边形,则CE=B´D.
1)当点B´在BE上时,BE=BB´+B´E=
2)当点B´在BE的延长线上时,BE=BB´-B´E=