

新高考数学一轮复习讲义 第8章 §8.5 椭圆及其性质
展开课本上和老师讲解的例题,一般都具有一定的典型性和代表性。要认真研究,深刻理解,要透过“样板”,学会通过逻辑思维,灵活运用所学知识去分析问题和解决问题,特别是要学习分析问题的思路、解决问题的方法,并能总结出解题的规律。
2、精练习题
复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性
每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。
4、重视错题
“错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
§8.5 椭圆及其性质
考试要求 1.理解椭圆的定义、几何图形、标准方程.2.掌握椭圆的简单几何性质(范围、对称性、顶点、离心率).3.掌握椭圆的简单应用.
知识梳理
1.椭圆的定义
把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.两个定点F1,F2叫做椭圆的焦点,两焦点间的距离|F1F2|叫做椭圆的焦距.
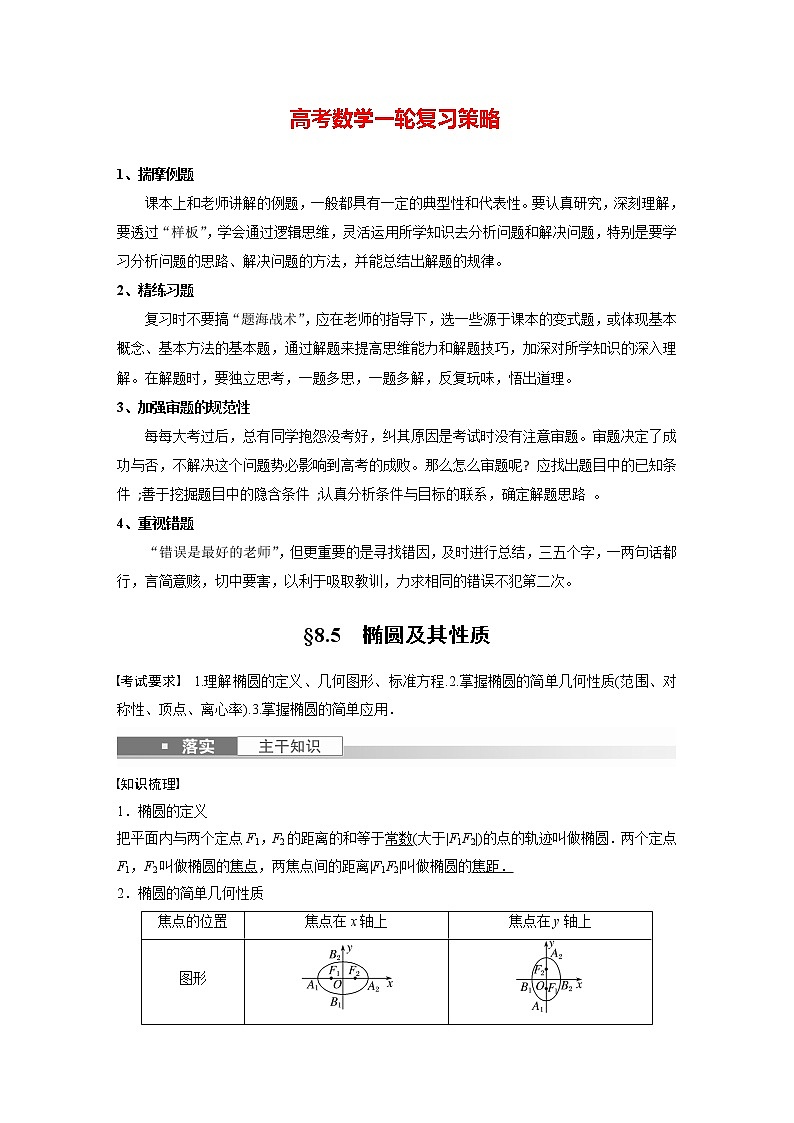
2.椭圆的简单几何性质
常用结论
椭圆的焦点三角形
椭圆上的点P(x0,y0)与两焦点构成的△PF1F2叫做焦点三角形.如图所示,设∠F1PF2=θ.
(1)当P为短轴端点时,θ最大,最大.
(2) =eq \f(1,2)|PF1||PF2|sin θ=b2tan eq \f(θ,2)=c|y0|.
(3)|PF1|max=a+c,|PF1|min=a-c.
(4)|PF1|·|PF2|≤eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(|PF1|+|PF2|,2)))2=a2.
(5)4c2=|PF1|2+|PF2|2-2|PF1||PF2|cs θ.
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭圆.( × )
(2)椭圆是轴对称图形,也是中心对称图形.( √ )
(3)eq \f(y2,m2)+eq \f(x2,n2)=1(m≠n)表示焦点在y轴上的椭圆.( × )
(4)eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)与eq \f(y2,a2)+eq \f(x2,b2)=1(a>b>0)的焦距相等.( √ )
教材改编题
1.设P是椭圆eq \f(x2,25)+eq \f(y2,16)=1上的点,若F1,F2是椭圆的两个焦点,则|PF1|+|PF2|等于( )
A.4 B.5 C.8 D.10
答案 D
解析 依椭圆的定义知,|PF1|+|PF2|=2×5=10.
2.若椭圆C:eq \f(x2,4)+eq \f(y2,3)=1,则该椭圆上的点到焦点距离的最大值为( )
A.3 B.2+eq \r(3)
C.2 D.eq \r(3)+1
答案 A
解析 由题意知a=2,b=eq \r(3),所以c=1,距离的最大值为a+c=3.
3.(2022·深圳模拟)已知椭圆C的焦点在x轴上,且离心率为eq \f(1,2),则C的方程可以为________.
答案 eq \f(x2,4)+eq \f(y2,3)=1(答案不唯一)
解析 因为焦点在x轴上,所以设椭圆的方程为eq \f(x2,a2)+eq \f(y2,b2)=1,a>b>0,
因为离心率为eq \f(1,2),
所以eq \f(c,a)=eq \f(1,2),
所以eq \f(c2,a2)=eq \f(a2-b2,a2)=eq \f(1,4),
则eq \f(b2,a2)=eq \f(3,4).
题型一 椭圆的定义及其应用
例1 (1)已知圆(x+2)2+y2=36的圆心为M,设A是圆上任意一点,N(2,0),线段AN的垂直平分线交MA于点P,则动点P的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
答案 B
解析 点P在线段AN的垂直平分线上,故|PA|=|PN|.又AM是圆的半径,所以|PM|+|PN|=|PM|+|PA|=|AM|=6>|MN|.由椭圆的定义知,P的轨迹是椭圆.
(2)设点P为椭圆C:eq \f(x2,a2)+eq \f(y2,4)=1(a>2)上一点,F1,F2分别为C的左、右焦点,且∠F1PF2=60°,则△PF1F2的面积为________.
答案 eq \f(4\r(3),3)
解析 由题意知,c=eq \r(a2-4).
又∠F1PF2=60°,|F1P|+|PF2|=2a,
|F1F2|=2eq \r(a2-4),
∴|F1F2|2=(|F1P|+|PF2|)2-2|F1P||PF2|-
2|F1P|·|PF2|cs 60°
=4a2-3|F1P|·|PF2|=4a2-16,
∴|F1P|·|PF2|=eq \f(16,3),
∴=eq \f(1,2)|F1P|·|PF2|sin 60°
=eq \f(1,2)×eq \f(16,3)×eq \f(\r(3),2)
=eq \f(4\r(3),3).
延伸探究 若将本例(2)中“∠F1PF2=60°”改成“PF1⊥PF2”,求△PF1F2的面积.
解 ∵PF1⊥PF2,
∴|PF1|2+|PF2|2=|F1F2|2=4(a2-4)
=4a2-16,
又|PF1|+|PF2|=2a,
∴|PF1|·|PF2|=8,
∴=4.
教师备选
1.△ABC的两个顶点为A(-3,0),B(3,0),△ABC周长为16,则顶点C的轨迹方程为( )
A.eq \f(x2,25)+eq \f(y2,16)=1(y≠0)B.eq \f(y2,25)+eq \f(x2,16)=1(y≠0)
C.eq \f(x2,16)+eq \f(y2,9)=1(y≠0)D.eq \f(y2,16)+eq \f(x2,9)=1(y≠0)
答案 A
解析 由题知点C到A,B两点的距离之和为10,故C的轨迹为以A(-3,0),B(3,0)为焦点,长轴长为10的椭圆,故2a=10,c=3,b2=a2-c2=16.所以方程为eq \f(x2,25)+eq \f(y2,16)=1.
又A,B,C三点不能共线,
所以eq \f(x2,25)+eq \f(y2,16)=1(y≠0).
2.若F1,F2是椭圆eq \f(x2,9)+eq \f(y2,7)=1的两个焦点,A为椭圆上一点,且∠AF1F2=45°,则△AF1F2的面积为( )
A.7 B.eq \f(7,4) C.eq \f(7,2) D.eq \f(7\r(5),2)
答案 C
解析 由题意得a=3,b=eq \r(7),c=eq \r(2),
∴|F1F2|=2eq \r(2),|AF1|+|AF2|=6.
∵|AF2|2=|AF1|2+|F1F2|2-2|AF1|·|F1F2|cs 45°
=|AF1|2+8-4|AF1|,
∴(6-|AF1|)2=|AF1|2+8-4|AF1|,
解得|AF1|=eq \f(7,2).
∴△AF1F2的面积
S=eq \f(1,2)×2eq \r(2)×eq \f(7,2)×eq \f(\r(2),2)=eq \f(7,2).
思维升华 椭圆定义的应用技巧
(1)椭圆定义的应用主要有:求椭圆的标准方程、求焦点三角形的周长、面积及求弦长、最值和离心率等.
(2)通常将定义和余弦定理结合使用求解关于焦点三角形的周长和面积问题.
跟踪训练1 (1)已知两圆C1:(x-4)2+y2=169,C2:(x+4)2+y2=9.动圆M在圆C1内部且和圆C1相内切,和圆C2相外切,则动圆圆心M的轨迹方程是( )
A.eq \f(x2,64)-eq \f(y2,48)=1B.eq \f(x2,48)+eq \f(y2,64)=1
C.eq \f(x2,48)-eq \f(y2,64)=1D.eq \f(x2,64)+eq \f(y2,48)=1
答案 D
解析 设动圆的圆心M(x,y),半径为r,
圆M与圆C1:(x-4)2+y2=169内切,
与圆C2:(x+4)2+y2=9外切.
所以|MC1|=13-r,|MC2|=3+r.
|MC1|+|MC2|=16>|C1C2|=8,
由椭圆的定义,M的轨迹是以C1,C2为焦点,长轴长为16的椭圆.
则a=8,c=4,所以b2=82-42=48,
动圆的圆心M的轨迹方程为eq \f(x2,64)+eq \f(y2,48)=1.
(2)(2022·武汉调研)设椭圆eq \f(x2,4)+eq \f(y2,3)=1的一个焦点为F,则对于椭圆上两动点A,B,△ABF周长的最大值为( )
A.4+eq \r(5) B.6
C.2eq \r(5)+2 D.8
答案 D
解析 设F1为椭圆的另外一个焦点,
则由椭圆的定义可得|AF|+|BF|+|AB|=2a-|AF1|+2a-|BF1|+|AB|=4a+|AB|-|BF1|-|AF1|=8+|AB|-|BF1|-|AF1|,
当A,B,F1三点共线时,
|AB|-|BF1|-|AF1|=0,
当A,B,F1三点不共线时,
|AB|-|BF1|-|AF1|<0,
所以当A,B,F1三点共线时,△ABF的周长取得最大值8.
题型二 椭圆的标准方程
命题点1 定义法
例2 已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( )
A.eq \f(x2,2)+y2=1 B.eq \f(x2,3)+eq \f(y2,2)=1
C.eq \f(x2,4)+eq \f(y2,3)=1 D.eq \f(x2,5)+eq \f(y2,4)=1
答案 B
解析 设椭圆的标准方程为eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0),
由椭圆定义可得|AF1|+|AB|+|BF1|=4a.
∵|AB|=|BF1|,∴|AF1|+2|AB|=4a.
又|AF2|=2|F2B|,
∴|AB|=eq \f(3,2)|AF2|,
∴|AF1|+3|AF2|=4a.
又|AF1|+|AF2|=2a,
∴|AF2|=a,∴A为椭圆的短轴端点.
如图,不妨设A(0,b),
又F2(1,0),eq \(AF2,\s\up6(—→))=2eq \(F2B,\s\up6(—→)),
∴Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2),-\f(b,2))).
将B点坐标代入椭圆方程eq \f(x2,a2)+eq \f(y2,b2)=1,
得eq \f(9,4a2)+eq \f(b2,4b2)=1,
∴a2=3,b2=a2-c2=2.
∴椭圆C的方程为eq \f(x2,3)+eq \f(y2,2)=1.
命题点2 待定系数法
例3 已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P1(eq \r(6),1),P2(-eq \r(3),-eq \r(2)),则该椭圆的方程为________.
答案 eq \f(x2,9)+eq \f(y2,3)=1
解析 设椭圆的方程为mx2+ny2=1(m>0,n>0,且m≠n).
因为椭圆经过P1,P2两点,
所以点P1,P2的坐标满足椭圆方程,
则eq \b\lc\{\rc\ (\a\vs4\al\c1(6m+n=1,,3m+2n=1,))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(m=\f(1,9),,n=\f(1,3).))
所以所求椭圆的方程为eq \f(x2,9)+eq \f(y2,3)=1.
教师备选
1.已知椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的左、右焦点分别为F1,F2,离心率为eq \f(1,2),过F2的直线与椭圆C交于A,B两点,若△F1AB的周长为8,则椭圆方程为( )
A.eq \f(x2,4)+eq \f(y2,3)=1 B.eq \f(x2,16)+eq \f(y2,12)=1
C.eq \f(x2,2)+y2=1 D.eq \f(x2,4)+eq \f(y2,2)=1
答案 A
解析 如图,
由椭圆的定义可知,△F1AB的周长为4a,
所以4a=8,a=2,又离心率为eq \f(1,2),
所以c=1,b2=3,
所以椭圆方程为eq \f(x2,4)+eq \f(y2,3)=1.
2.设椭圆eq \f(x2,m2)+eq \f(y2,n2)=1(m>0,n>0)的右焦点为(2,0),离心率为eq \f(\r(2),2),则此椭圆的方程为________.
答案 eq \f(x2,8)+eq \f(y2,4)=1
解析 椭圆的右焦点为(2,0),
所以m2-n2=4,e=eq \f(\r(2),2)=eq \f(2,m),
所以m=2eq \r(2),代入m2-n2=4,得n2=4,
所以椭圆方程为eq \f(x2,8)+eq \f(y2,4)=1.
思维升华 根据条件求椭圆方程的主要方法
(1)定义法:根据题目所给条件确定动点的轨迹满足椭圆的定义.
(2)待定系数法:根据题目所给的条件确定椭圆中的a,b.当不知焦点在哪一个坐标轴上时,一般可设所求椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n),不必考虑焦点位置,用待定系数法求出m,n的值即可.
跟踪训练2 (1)已知椭圆的两个焦点为F1(-eq \r(5),0),F2(eq \r(5),0),M是椭圆上一点,若MF1⊥MF2,|MF1|·|MF2|=8,则该椭圆的方程是( )
A.eq \f(x2,7)+eq \f(y2,2)=1 B.eq \f(x2,2)+eq \f(y2,7)=1
C.eq \f(x2,9)+eq \f(y2,4)=1 D.eq \f(x2,4)+eq \f(y2,9)=1
答案 C
解析 设|MF1|=m,|MF2|=n,
因为MF1⊥MF2,|MF1|·|MF2|=8,
|F1F2|=2eq \r(5),
所以m2+n2=20,mn=8,
所以(m+n)2=36,
所以m+n=2a=6,所以a=3.
因为c=eq \r(5),
所以b=eq \r(a2-c2)=2.
所以椭圆的方程是eq \f(x2,9)+eq \f(y2,4)=1.
(2)已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线交C于A,B两点,且|AB|=3,则C的方程为( )
A.eq \f(x2,2)+y2=1 B.eq \f(x2,3)+eq \f(y2,2)=1
C.eq \f(x2,4)+eq \f(y2,3)=1 D.eq \f(x2,5)+eq \f(y2,4)=1
答案 C
解析 如图,|AF2|=eq \f(1,2)|AB|=eq \f(3,2),|F1F2|=2,
由椭圆定义,得|AF1|=2a-eq \f(3,2).①
在Rt△AF1F2中,
|AF1|2=|AF2|2+|F1F2|2=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))2+22.②
由①②得a=2,∴b2=a2-c2=3.
∴椭圆C的方程为eq \f(x2,4)+eq \f(y2,3)=1.
题型三 椭圆的几何性质
命题点1 离心率
例4 (1)(2022·湛江模拟)已知F是椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的右焦点,过椭圆C的下顶点且斜率为eq \f(3,4)的直线与以点F为圆心、半焦距为半径的圆相切,则椭圆C的离心率为( )
A.eq \f(\r(5),5) B.eq \f(1,2)
C.eq \f(\r(3),3) D.eq \f(\r(2),2)
答案 A
解析 过椭圆C的下顶点(0,-b)且斜率为eq \f(3,4)的直线方程为y=eq \f(3,4)x-b,即eq \f(3,4)x-y-b=0,
F(c,0),由点到直线距离公式,
得c=eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(\f(3,4)c-b)),\r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4)))2+1)),
即c2=-eq \f(3,2)bc+b2,即(2c-b)(c+2b)=0,
则2c-b=0,b=2c.
又a2=b2+c2,即a2=(2c)2+c2=5c2,
解得eq \f(c,a)=eq \f(\r(5),5).
(2)已知F1,F2分别是椭圆eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的左、右焦点,若椭圆上存在点P,使∠F1PF2=90°,则椭圆的离心率e的取值范围为( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(\r(2),2))) B.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(2),2),1))
C.eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(\r(3),2))) D.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(3),2),1))
答案 B
解析 若椭圆上存在点P,使得PF1⊥PF2,则以原点为圆心,F1F2为直径的圆与椭圆必有交点,如图,
可得c≥b,即c2≥b2,
所以2c2≥a2,即e2≥eq \f(1,2),
又e<1,所以e∈eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(2),2),1)).
思维升华 求椭圆离心率或其范围的方法
(1)直接求出a,c,利用离心率公式e=eq \f(c,a)求解.
(2)由a与b的关系求离心率,利用变形公式e=eq \r(1-\f(b2,a2))求解.
(3)构造a,c的齐次式.可以不求出a,c的具体值,而是得出a与c的关系,从而求得e.
命题点2 与椭圆有关的范围(最值)
例5 (1)以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1,则椭圆长轴长的最小值为( )
A.1 B.eq \r(2) C.2 D.2eq \r(2)
答案 D
解析 设a,b,c分别为椭圆的长半轴长、短半轴长、半焦距,依题意知,当三角形的高为b时,以椭圆上一点和两个焦点为顶点的三角形的面积最大,所以eq \f(1,2)×2cb=1,故bc=1,故2a=2eq \r(b2+c2)≥2eq \r(2bc)=2eq \r(2)(当且仅当b=c=1时取等号).
(2)如图,焦点在x轴上的椭圆eq \f(x2,4)+eq \f(y2,b2)=1(b>0)的离心率e=eq \f(1,2),F,A分别是椭圆的左焦点和右顶点,P是椭圆上任意一点,则eq \(PF,\s\up6(→))·eq \(PA,\s\up6(→))的最大值为________.
答案 4
解析 由题意知a=2,因为e=eq \f(c,a)=eq \f(1,2),
所以c=1,
所以b2=a2-c2=3,
故椭圆的方程为eq \f(x2,4)+eq \f(y2,3)=1.
设P点的坐标为(x0,y0),
所以-2≤x0≤2,-eq \r(3)≤y0≤eq \r(3).
因为F(-1,0),A(2,0),
所以eq \(PF,\s\up6(→))=(-1-x0,-y0),
eq \(PA,\s\up6(→))=(2-x0,-y0),
所以eq \(PF,\s\up6(→))·eq \(PA,\s\up6(→))=xeq \\al(2,0)-x0-2+yeq \\al(2,0)=eq \f(1,4)xeq \\al(2,0)-x0+1=eq \f(1,4)(x0-2)2,
所以当x0=-2时,eq \(PF,\s\up6(→))·eq \(PA,\s\up6(→))取得最大值4.
教师备选
1.(多选)嫦娥四号在绕月飞行时是以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为100公里,远月点与月球表面距离为400公里,已知月球的直径约为3 476公里,则下列选项中正确的有( )
A.焦距长约为300公里
B.长轴长约为3 988公里
C.两焦点坐标约为(±150,0)
D.离心率约为eq \f(75,994)
答案 AD
解析 设该椭圆的长半轴长为a,半焦距长为c.
依题意可得月球半径约为eq \f(1,2)×3 476=1 738,
a-c=100+1 738=1 838,
a+c=400+1 738=2 138,
所以2a=1 838+2 138=3 976,a=1 988,
c=2 138-1 988=150,2c=300,
椭圆的离心率约为e=eq \f(c,a)=eq \f(150,1 988)=eq \f(75,994),
可得结论A,D正确,B错误;因为没有给坐标系,焦点坐标不确定,所以C错误.
2.(2022·太原模拟)若点O和点F分别为椭圆eq \f(x2,4)+eq \f(y2,3)=1的中心和左焦点,点P为椭圆上的任意一点,则eq \(OP,\s\up6(→))·eq \(FP,\s\up6(→))的最大值为( )
A.2 B.3 C.6 D.8
答案 C
解析 由椭圆eq \f(x2,4)+eq \f(y2,3)=1可得F(-1,0),
点O(0,0).
设P(x,y)(-2≤x≤2).
则eq \(OP,\s\up6(→))·eq \(FP,\s\up6(→))=x2+x+y2=x2+x+3eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(x2,4)))
=eq \f(1,4)x2+x+3=eq \f(1,4)(x+2)2+2,-2≤x≤2,
当且仅当x=2时,eq \(OP,\s\up6(→))·eq \(FP,\s\up6(→))取得最大值6.
思维升华 与椭圆有关的最值或范围问题的求解方法
(1)利用数形结合、几何意义,尤其是椭圆的性质;
(2)利用函数,尤其是二次函数;
(3)利用不等式,尤其是基本不等式.
跟踪训练3 (1)(2022·济南质检)设椭圆E的两焦点分别为F1,F2,以F1为圆心,|F1F2|为半径的圆与E交于P,Q两点.若△PF1F2为直角三角形,则E的离心率为( )
A.eq \r(2)-1 B.eq \f(\r(5)-1,2)
C.eq \f(\r(2),2) D.eq \r(2)+1
答案 A
解析 不妨设椭圆E的方程为eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0),如图所示,∵△PF1F2为直角三角形,∴PF1⊥F1F2,又|PF1|=|F1F2|=2c,∴|PF2|=2eq \r(2)c,∴|PF1|+|PF2|=2c+2eq \r(2)c=2a,
∴椭圆E的离心率e=eq \f(c,a)=eq \r(2)-1.
(2)已知椭圆eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的右焦点为F(c,0),上顶点为A(0,b),直线x=eq \f(a2,c)上存在一点P满足(eq \(FP,\s\up6(→))+eq \(FA,\s\up6(→)))·eq \(AP,\s\up6(→))=0,则椭圆的离心率的取值范围为( )
A.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,2),1)) B.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(2),2),1))
C.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(5)-1,2),1)) D.eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(\r(2),2)))
答案 C
解析 取AP的中点Q,则eq \(FQ,\s\up6(→))=eq \f(1,2)(eq \(FP,\s\up6(→))+eq \(FA,\s\up6(→))),
所以(eq \(FP,\s\up6(→))+eq \(FA,\s\up6(→)))·eq \(AP,\s\up6(→))=2eq \(FQ,\s\up6(→))·eq \(AP,\s\up6(→))=0,
所以FQ⊥AP,所以△AFP为等腰三角形,
即|FA|=|FP|,且|FA|=eq \r(b2+c2)=a.
因为点P在直线x=eq \f(a2,c)上,
所以|FP|≥eq \f(a2,c)-c,即a≥eq \f(a2,c)-c,
所以eq \f(a,c)≥eq \f(a2,c2)-1,所以e2+e-1≥0,
解得e≥eq \f(\r(5)-1,2)或e≤eq \f(-\r(5)-1,2).
又0<e<1,故eq \f(\r(5)-1,2)≤e<1.
课时精练
1.已知动点M到两个定点A(-2,0),B(2,0)的距离之和为6,则动点M的轨迹方程为( )
A.eq \f(x2,9)+y2=1 B.eq \f(y2,9)+eq \f(x2,5)=1
C.eq \f(y2,9)+x2=1 D.eq \f(x2,9)+eq \f(y2,5)=1
答案 D
解析 由题意有6>2+2=4,
故点M的轨迹为焦点在x轴上的椭圆,
则2a=6,c=2,故a2=9,
所以b2=a2-c2=5,
故椭圆的方程为eq \f(x2,9)+eq \f(y2,5)=1.
2.若椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的短轴长等于焦距,则椭圆的离心率为( )
A.eq \f(1,2) B.eq \f(\r(3),3)
C.eq \f(\r(2),2) D.eq \f(\r(2),4)
答案 C
解析 依题意可知,c=b,
又a=eq \r(b2+c2)=eq \r(2)c,
∴椭圆的离心率e=eq \f(c,a)=eq \f(\r(2),2).
3.椭圆eq \f(x2,2)+y2=1的两个焦点分别是F1,F2,点P是椭圆上任意一点,则eq \(PF1,\s\up6(—→))·eq \(PF2,\s\up6(—→))的取值范围是( )
A.[-1,1] B.[-1,0]
C.[0,1] D.[-1,2]
答案 C
解析 设F1为左焦点,
则由椭圆方程得F1(-1,0),F2(1,0),
设P(x,y),-eq \r(2)≤x≤eq \r(2),
∴eq \(PF1,\s\up6(—→))=(-1-x,-y),eq \(PF2,\s\up6(—→))=(1-x,-y),
则eq \(PF1,\s\up6(—→))·eq \(PF2,\s\up6(—→))=x2+y2-1=eq \f(x2,2)∈[0,1].
4.设e是椭圆eq \f(x2,4)+eq \f(y2,k)=1的离心率,且e∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1)),则实数k的取值范围是( )
A.(0,3) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(3,\f(16,3)))
C.(0,3)∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(16,3),+∞)) D.(0,2)
答案 C
解析 当k>4时,c=eq \r(k-4),
由条件知eq \f(1,4)
当0
A.椭圆C的方程为eq \f(y2,3)+x2=1
B.椭圆C的方程为eq \f(x2,3)+y2=1
C.|PQ|=eq \f(2\r(3),3)
D.△PF2Q的周长为4eq \r(3)
答案 ACD
解析 由已知得,
2b=2,b=1,eq \f(c,a)=eq \f(\r(6),3),
又a2=b2+c2,解得a2=3.
∴椭圆方程为x2+eq \f(y2,3)=1,
如图.
∴|PQ|=eq \f(2b2,a)=eq \f(2,\r(3))=eq \f(2\r(3),3),
△PF2Q的周长为4a=4eq \r(3).
6.(多选)(2022·济南模拟)已知椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,1)在椭圆内部,点Q在椭圆上,则以下说法正确的是( )
A.|QF1|+|QP|的最小值为2a-1
B.椭圆C的短轴长可能为2
C.椭圆C的离心率的取值范围为eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(\r(5)-1,2)))
D.若eq \(PF1,\s\up6(—→))=eq \(F1Q,\s\up6(—→)),则椭圆C的长轴长为eq \r(5)+eq \r(17)
答案 ACD
解析 由题意可知2c=2,则c=1,因为点Q在椭圆上,
所以|QF1|+|QF2|=2a,|QF1|+|QP|=2a-|QF2|+|QP|,
又-1≤-|QF2|+|QP|≤1,所以A正确;
因为点P(1,1)在椭圆内部,所以b>1,2b>2,
所以B错误;
因为点P(1,1)在椭圆内部,所以eq \f(1,a2)+eq \f(1,b2)<1,
即b2+a2-a2b2<0,又c=1,b2=a2-c2,
所以(a2-1)+a2-a2(a2-1)<0,
化简可得a4-3a2+1>0(a>1),
解得a2>eq \f(3+\r(5),2)或a2<eq \f(3-\r(5),2)(舍去),
则椭圆C的离心率
e=eq \f(c,a)<eq \f(1,\r(\f(3+\r(5),2)))=eq \f(1,\f(\r(5)+1,2))=eq \f(\r(5)-1,2),
又0
由eq \(PF1,\s\up6(—→))=eq \(F1Q,\s\up6(—→))可得,F1为PQ的中点,
而P(1,1),F1(-1,0),
所以Q(-3,-1),
|QF1|+|QF2|
=eq \r(-3+12+-1-02)+eq \r(-3-12+-1-02)
=eq \r(5)+eq \r(17)=2a,
所以D正确.
7.如图是篮球在太阳光照射下的影子,已知篮球的直径为22 cm,现太阳光与地面的夹角为60°,则此椭圆形影子的离心率为________.
答案 eq \f(1,2)
解析 由图可得,椭圆的短轴长2b=22⇒b=11,
2a=eq \f(22,sin 60°)=eq \f(22,\f(\r(3),2))⇒a=eq \f(22,\r(3)),
∴e=eq \f(c,a)=eq \r(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(b,a)))2)=eq \r(1-\f(3,4))=eq \f(1,2).
8.(2021·全国甲卷)已知F1,F2为椭圆C:eq \f(x2,16)+eq \f(y2,4)=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2|,则四边形PF1QF2的面积为________.
答案 8
解析 根据椭圆的对称性及|PQ|=|F1F2|可以得到四边形PF1QF2为对角线相等的平行四边形,所以四边形PF1QF2为矩形.设|PF1|=m,则|PF2|=2a-|PF1|=8-m,则|PF1|2+|PF2|2=m2+(8-m)2=2m2+64-16m=|F1F2|2=4c2=4(a2-b2)=48,
得m(8-m)=8,所以四边形PF1QF2的面积为
|PF1|×|PF2|=m(8-m)=8.
9.已知椭圆的长轴长为10,两焦点F1,F2的坐标分别为(3,0)和(-3,0).
(1)求椭圆的标准方程;
(2)若P为短轴的一个端点,求△F1PF2的面积.
解 (1)设椭圆的标准方程为
eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0),
依题意得eq \b\lc\{\rc\ (\a\vs4\al\c1(2a=10,,c=3,))
因此a=5,b=4,
所以椭圆的标准方程为eq \f(x2,25)+eq \f(y2,16)=1.
(2)易知|yP|=4,又c=3,
所以=eq \f(1,2)|yP|×2c=eq \f(1,2)×4×6=12.
10.已知椭圆C:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0),焦点F1(-c,0),F2(c,0),左顶点为A,点E的坐标为(0,c),A到直线EF2的距离为eq \f(\r(6),2)b.
(1)求椭圆C的离心率;
(2)若P为椭圆C上的一点,∠F1PF2=60°,△PF1F2的面积为eq \r(3),求椭圆C的方程.
解 (1)由题意得,A(-a,0),EF2:x+y=c,
因为A到直线EF2的距离为eq \f(\r(6),2)b,
即eq \f(|-a-c|,\r(12+12))=eq \f(\r(6),2)b,
所以a+c=eq \r(3)b,
即(a+c)2=3b2,又b2=a2-c2,
所以(a+c)2=3(a2-c2),
所以2c2+ac-a2=0,
因为离心率e=eq \f(c,a),
所以2e2+e-1=0,
解得e=eq \f(1,2)或e=-1(舍),
所以椭圆C的离心率为eq \f(1,2).
(2)由(1)知离心率e=eq \f(c,a)=eq \f(1,2),即a=2c,①
因为∠F1PF2=60°,△PF1F2的面积为eq \r(3),
则eq \f(1,2)|PF1||PF2|sin 60°=eq \r(3),
所以|PF1||PF2|=4,
又eq \b\lc\{\rc\ (\a\vs4\al\c1(|PF1|+|PF2|=2a,,|PF1|2+|PF2|2-2|PF1||PF2|cs 60°=2c2,))
所以a2-c2=3,②
联立①②得a=2,c=1,所以b2=a2-c2=3,
所以椭圆C的标准方程为eq \f(x2,4)+eq \f(y2,3)=1.
11.(多选)(2022·大连模拟)已知椭圆C:eq \f(x2,16)+eq \f(y2,9)=1的左、右焦点分别是F1,F2,左、右顶点分别是A1,A2,点P是椭圆C上异于A1,A2的任意一点,则下列说法正确的是( )
A.|PF1|+|PF2|=4
B.存在点P满足∠F1PF2=90°
C.直线PA1与直线PA2的斜率之积为-eq \f(9,16)
D.若△F1PF2的面积为2eq \r(7),则点P的横坐标为±eq \f(4\r(5),3)
答案 CD
解析 由椭圆方程知a=4,b=3,c=eq \r(7),
|PF1|+|PF2|=2a=8,A错误;
当P在椭圆上、下顶点时,
cs∠F1PF2=eq \f(2a2-4c2,2a2)=eq \f(1,8)>0,
即∠F1PF2最大值小于eq \f(π,2),B错误;
若P(x′,y′),则 =eq \f(y′,x′+4),
=eq \f(y′,x′-4),
有=eq \f(y′2,x′2-16),
而eq \f(x′2,16)+eq \f(y′2,9)=1,
所以-16y′2=9(x′2-16),
即有=-eq \f(9,16),C正确;
若P(x′,y′),△F1PF2的面积为2eq \r(7),
即eq \f(2c·|y′|,2)=2eq \r(7),
故y′=±2,
代入椭圆方程得x′=±eq \f(4\r(5),3),D正确.
12.(多选)2021年10月16日,神舟十三号发射圆满成功,人民日报微博发了一条“跨越时空的同一天”,致敬每一代人的拼搏!已知飞船在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即飞船的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为2a,2c,下列结论正确的是( )
A.飞船向径的取值范围是[a-c,a+c]
B.飞船在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间
C.飞船向径的最小值与最大值的比值越大,椭圆轨道越扁
D.飞船运行速度在近地点时最大,在远地点时最小
答案 ABD
解析 根据椭圆定义知飞船向径的取值范围是[a-c,a+c],A正确;
当飞船在左半椭圆弧上运行时,对应的面积更大,根据面积守恒规律,知在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间,B正确;
eq \f(a-c,a+c)=eq \f(1-e,1+e)=eq \f(2,1+e)-1,比值越大,则e越小,椭圆轨道越圆,C错误;
根据面积守恒规律,飞船在近地点时向径最小,故速度最大,在远地点时向径最大,故速度最小,D正确.
13.设F1,F2分别是椭圆eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的左、右焦点,若在直线x=eq \f(a2,c)上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(\r(2),2))) B.eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(\r(3),3))) C.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(2),2),1)) D.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(\r(3),3),1))
答案 D
解析 设Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a2,c),m)),F1(-c,0),F2(c,0),
由线段PF1的中垂线过点F2得
|PF2|=|F1F2|,
即 eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(a2,c)-c))2+m2)=2c,
得m2=4c2-eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a2,c)-c))2=-eq \f(a4,c2)+2a2+3c2≥0,
即3c4+2a2c2-a4≥0,
得3e4+2e2-1≥0,解得e2≥eq \f(1,3),
又0
答案 eq \f(2\r(5),5) eq \f(\r(5),5)
解析 设过F1的直线与圆的切点为M,圆心Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)c,0)),
则|AM|=c,|AF1|=eq \f(3,2)c,
所以|MF1|=eq \f(\r(5),2)c,
所以该直线的斜率k=eq \f(|AM|,|MF1|)=eq \f(c,\f(\r(5),2)c)=eq \f(2\r(5),5).
因为PF2⊥x轴,所以|PF2|=eq \f(b2,a),
又|F1F2|=2c,
所以k=eq \f(2\r(5),5)=eq \f(\f(b2,a),2c)=eq \f(a2-c2,2ac)=eq \f(1-e2,2e)(0
15.已知椭圆eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)的短轴长为2,上顶点为A,左顶点为B,左、右焦点分别为F1,F2,且△F1AB的面积为eq \f(2-\r(3),2),若点P为椭圆上的任意一点,则eq \f(1,|PF1|)+eq \f(1,|PF2|)的取值范围是________.
答案 [1,4]
解析 由已知得2b=2,故b=1.
∵△F1AB的面积为eq \f(2-\r(3),2),
∴eq \f(1,2)(a-c)b=eq \f(2-\r(3),2),
∴a-c=2-eq \r(3),
又a2-c2=(a-c)(a+c)=b2=1,
∴a=2,c=eq \r(3),
∴eq \f(1,|PF1|)+eq \f(1,|PF2|)
=eq \f(|PF1|+|PF2|,|PF1||PF2|)
=eq \f(2a,|PF1|2a-|PF1|)
=eq \f(4,-|PF1|2+4|PF1|).
又2-eq \r(3)≤|PF1|≤2+eq \r(3),
∴1≤-|PF1|2+4|PF1|≤4,
∴1≤eq \f(1,|PF1|)+eq \f(1,|PF2|)≤4,
即eq \f(1,|PF1|)+eq \f(1,|PF2|)的取值范围为[1,4].
16.已知F1,F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.
(1)求椭圆的离心率的取值范围;
(2)求证:△F1PF2的面积只与椭圆的短轴长有关.
(1)解 不妨设椭圆的方程为eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0),焦距为2c.
在△F1PF2中,由余弦定理得,
cs 60°=eq \f(|PF1|2+|PF2|2-|F1F2|2,2|PF1|·|PF2|)
=eq \f(|PF1|+|PF2|2-2|PF1|·|PF2|-|F1F2|2,2|PF1|·|PF2|),
即eq \f(4a2-2|PF1|·|PF2|-4c2,2|PF1|·|PF2|)=eq \f(1,2),
所以|PF1|·|PF2|=4a2-2|PF1|·|PF2|-4c2,
所以3|PF1|·|PF2|=4b2,
所以|PF1|·|PF2|=eq \f(4b2,3).
又因为|PF1|·|PF2|≤eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(|PF1|+|PF2|,2)))2=a2,
当且仅当|PF1|=|PF2|时等号成立,
所以3a2≥4(a2-c2),
所以eq \f(c,a)≥eq \f(1,2),
所以e≥eq \f(1,2).
又因为0
(2)证明 由(1)可知|PF1|·|PF2|=eq \f(4,3)b2,
所以=eq \f(1,2)|PF1|·|PF2|sin 60°
=eq \f(1,2)×eq \f(4,3)b2×eq \f(\r(3),2)
=eq \f(\r(3),3)b2,
所以△F1PF2的面积只与椭圆的短轴长有关.焦点的位置
焦点在x轴上
焦点在y轴上
图形
标准方程
eq \f(x2,a2)+eq \f(y2,b2)=1 (a>b>0)
eq \f(y2,a2)+eq \f(x2,b2)=1 (a>b>0)
范围
-a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
顶点
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),
A2(0,a)
B1(-b,0),
B2(b,0)
轴长
短轴长为2b,长轴长为2a
焦点
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
焦距
|F1F2|=2c
对称性
对称轴:x轴和y轴,对称中心:原点
离心率
e=eq \f(c,a)(0
a2=b2+c2
(新高考)高考数学一轮复习学案+巩固提升练习8.5《椭圆及其性质》(2份打包,原卷版+教师版): 这是一份(新高考)高考数学一轮复习学案+巩固提升练习8.5《椭圆及其性质》(2份打包,原卷版+教师版),文件包含新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》原卷版doc、新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》原卷版pdf、新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》教师版doc、新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》教师版pdf等4份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。
(新高考)高考数学一轮复习学案+分层提升8.5《椭圆及其性质》(2份打包,原卷版+教师版): 这是一份(新高考)高考数学一轮复习学案+分层提升8.5《椭圆及其性质》(2份打包,原卷版+教师版),文件包含新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》原卷版doc、新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》原卷版pdf、新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》教师版doc、新高考高考数学一轮复习讲义+巩固练习85《椭圆及其性质》教师版pdf等4份试卷配套教学资源,其中试卷共65页, 欢迎下载使用。
新高考数学一轮复习讲义9.5《椭圆第1课时椭圆及其性质 》(2份打包,解析版+原卷版): 这是一份新高考数学一轮复习讲义9.5《椭圆第1课时椭圆及其性质 》(2份打包,解析版+原卷版),文件包含新高考数学一轮复习讲义95《椭圆第1课时椭圆及其性质》含详解doc、新高考数学一轮复习讲义95《椭圆第1课时椭圆及其性质》原卷版doc等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。












