资料中包含下列文件，点击文件名可预览资料内容
还剩23页未读，
继续阅读
所属成套资源：中考数学二轮复习专题（共54讲）
成套系列资料，整套一键下载
中考数学专题复习 专题32 中考几何平移类问题
展开
这是一份中考数学专题复习 专题32 中考几何平移类问题，文件包含中考数学专题复习专题32中考几何平移类问题教师版含解析docx、中考数学专题复习专题32中考几何平移类问题学生版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
从分析问题的数量关系入手，适当设定未知数，把所研究的数学问题中已知量和未知量之间的数量关系，转化为方程或方程组的数学模型，从而使问题得到解决的思维方法
2、学会运用数形结合思想。
数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。
一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。
在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。
如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:
体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
专题32 中考几何平移类问题
1.平移的定义：平面图形的每个点沿着某一方向移动相同的距离，这样的图形运动称为平移.平移是由移动的方向和移动的距离所决定.平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。
2.平移的特点：经平移运动后的图形图形的位置发生变化, 形状和大小不变.
3.理解并掌握平移的三个特征：
(1)对应线段平行(或在一条直线上)且相等；对应角相等.
(2)对应点所连的线段平行(或在一条直线上)且相等.
(3)图形在平移后形状和大小都不变.
4.图形平移的画法：
(1)确定点；(2)定方向；(3)定距离。
【例题1】(2020•广东)在平面直角坐标系中，点(3，2)关于x轴对称的点的坐标为( )
A．(﹣3，2)B．(﹣2，3)C．(2，﹣3)D．(3，﹣2)
【对点练习】(2019湖南邵阳)一次函数y1=k1x+b1的图象l1如图所示，将直线l1向下平移若干个单位后得直线l2，l2的函数表达式为y2=k2x+b2．下列说法中错误的是( )
A．k1=k2 B．b1＜b2
C．b1＞b2 D．当x=5时，y1＞y2
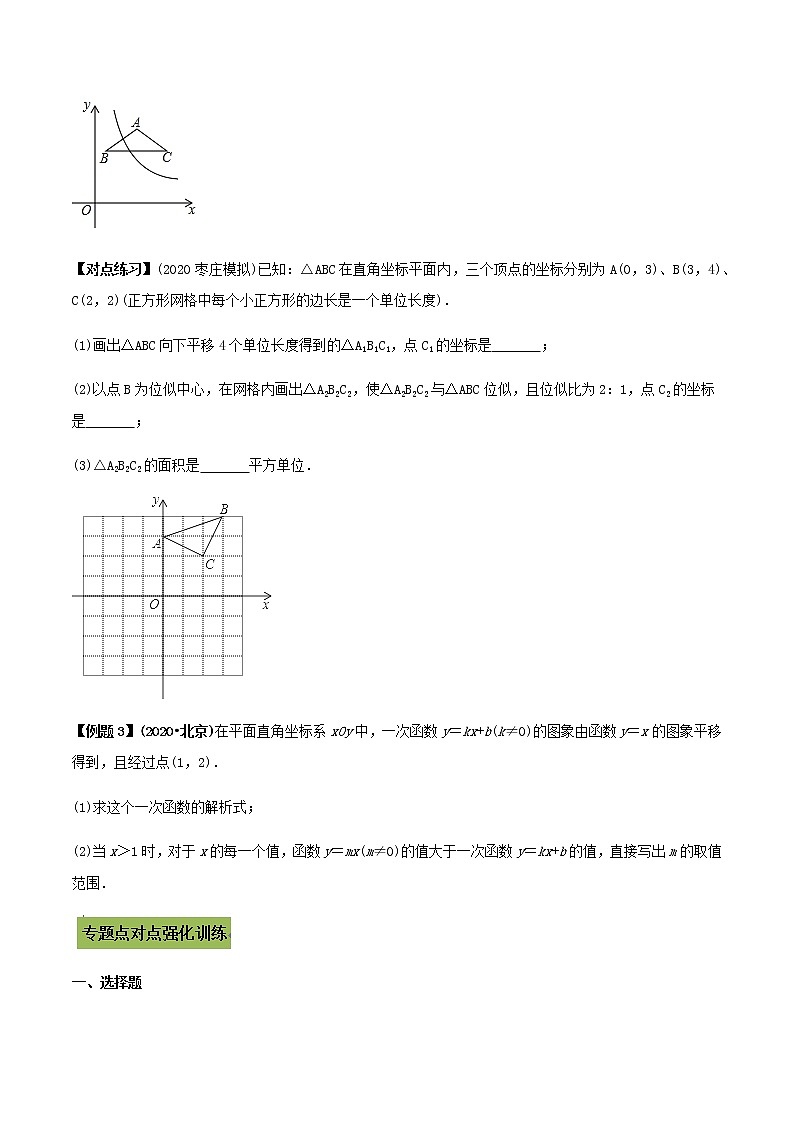
【例题2】(2019桂林)如图，在平面直角坐标系中，反比例y＝(k＞0)的图象和△ABC都在第一象限内，AB＝AC＝，BC∥x轴，且BC＝4，点A的坐标为(3，5)．若将△ABC向下平移m个单位长度，A，C两点同时落在反比例函数图象上，则m的值为 ．
【对点练习】(2020枣庄模拟)已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A(0，3)、B(3，4)、C(2，2)(正方形网格中每个小正方形的边长是一个单位长度)．
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；
(2)以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是 ；
(3)△A2B2C2的面积是 平方单位．
【例题3】(2020•北京)在平面直角坐标系xOy中，一次函数y＝kx+b(k≠0)的图象由函数y＝x的图象平移得到，且经过点(1，2)．
(1)求这个一次函数的解析式；
(2)当x＞1时，对于x的每一个值，函数y＝mx(m≠0)的值大于一次函数y＝kx+b的值，直接写出m的取值范围．
一、选择题
1．(2020•菏泽)在平面直角坐标系中，将点P(﹣3，2)向右平移3个单位得到点P'，则点P'关于x轴的对称点的坐标为( )
A．(0，﹣2)B．(0，2)C．(﹣6，2)D．(﹣6，﹣2)
2.(2019哈尔滨)将抛物线向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线
为( )
A． B．
C． D．
3．(2019海南)如图，在平面直角坐标系中，已知点A(2，1)，点B(3，﹣1)，平移线段AB，使点A落在点A1(﹣2，2)处，则点B的对应点B1的坐标为( )
A．(﹣1，﹣1)B．(1，0)C．(﹣1，0)D．(3，0)
4．(2019广西梧州)直线y＝3x+1向下平移2个单位，所得直线的解析式是( )
A．y＝3x+3B．y＝3x﹣2C．y＝3x+2D．y＝3x﹣1
5．(2019广西百色)抛物线y＝x2+6x+7可由抛物线y＝x2如何平移得到的( )
A．先向左平移3个单位，再向下平移2个单位
B．先向左平移6个单位，再向上平移7个单位
C．先向上平移2个单位，再向左平移3个单位
D．先回右平移3个单位，再向上平移2个单位
6．(2020济南模拟)如图，在平面直角坐标系中，△ABC的顶点都在方格纸的格点上，如果将△ABC先向右平移4个单位长度，在向下平移1个单位长度，得到△A1B1C1，那么点A的对应点A1的坐标为( )
A．(4，3)B．(2，4)C．(3，1)D．(2，5)
7.将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式
为( )
A．y=(x﹣1)2+4B．y=(x﹣4)2+4C．y=(x+2)2+6D．y=(x﹣4)2+6
8．(2020咸宁模拟)如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为( )
9.如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为( )
A．48B．96C．84D．42
10.某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是( )
A．甲种方案所用铁丝最长B．乙种方案所用铁丝最长
C．丙种方案所用铁丝最长D．三种方案所用铁丝一样长
二、填空题
11．(2020•武威)如图，在平面直角坐标系中，△OAB的顶点A，B的坐标分别为(3，3)，(4，0)．把△OAB沿x轴向右平移得到△CDE，如果点D的坐标为(6，3)，则点E的坐标为 ．
12．(2020枣庄模拟)如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为 ．
13．(2020咸宁模拟)如图，在平面直角坐标系中，点A的坐标为(0，6)，将△OAB沿x轴向左平移得到△O′A′B′，点A的对应点A′落在直线y=﹣x上，则点B与其对应点B′间的距离为 ．
14．(2020岳阳模拟)如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论正确的是 ．(写出所有正确结论的序号)
①b＞0
②a﹣b+c＜0
③阴影部分的面积为4
④若c=﹣1，则b2=4a．
15.如图所示，一座楼房的楼梯，高1米，水平距离是2.8米，如果要在台阶上铺一种地毯，那么至少要买这种地毯________米．
16.如图，是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片，经测得FG＝9cm，则这个剪出的图形的周长是________cm．
17．如图，若△DEF是由△ABC经过平移后得到的，则平移的距离是_____．
18．(2019江苏徐州)已知二次函数的图象经过点P(2，2)，顶点为O(0，0)将该图象向右平移，当它再次经过点P时，所得抛物线的函数表达式为 ．
三、解答题
19．(2020•安顺)如图，一次函数y＝x+1的图象与反比例函数y=kx的图象相交，其中一个交点的横坐标
是2．
(1)求反比例函数的表达式；
(2)将一次函数y＝x+1的图象向下平移2个单位，求平移后的图象与反比例函数y=kx图象的交点坐标；
(3)直接写出一个一次函数，使其过点(0，5)，且与反比例函数y=kx的图象没有公共点．
20．(2020齐齐哈尔模拟)如图，在边上为1个单位长度的小正方形网格中：
(1)画出△ABC向上平移6个单位长度，再向右平移5个单位长度后的△A1B1C1．
(2)以点B为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2．
(3)求△CC1C2的面积．
21.(2020浙江宁波模拟)已知抛物线，其中是常数
(1)求证：不论为何值，该抛物线与轴一定有两个公共点；
(2)若该抛物线的对称轴为直线，
①求该抛物线的函数解析式；
②把该抛物线沿轴向上平移多少个单位长度后，得到的抛物线与轴只有一个公共点？
22.如图，在一块长为20m，宽为14m的草地上有一条宽为2m的曲折小路，你能运用你学的知识求出这块草地的绿地面积吗？
23．如图所示，将△ABC平移，可以得到△DEF，点B的对应点为点E，请画出点A的对应点D、点C的对应点F的位置，并作出△DEF．
24．如图，将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF，则四边形ABFD的周长?
25．如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．求证：BE=DG
26.如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A(﹣1，3)，B(﹣4，0)，C(0，0)。画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1。
27.如图，在一块长为20m，宽为14m的草地上有一条宽为2m的曲折小路，你能运用你学的知识求出这块草地的绿地面积吗？
28．(2019宁夏)将直角三角板ABC按如图1放置，直角顶点C与坐标原点重合，直角边AC、BC分别与x轴和y轴重合，其中∠ABC＝30°．将此三角板沿y轴向下平移，当点B平移到原点O时运动停止．设平移的距离为m，平移过程中三角板落在第一象限部分的面积为s，s关于m的函数图象(如图2所示)与m轴相交于点P(，0)，与s轴相交于点Q．
(1)试确定三角板ABC的面积；
(2)求平移前AB边所在直线的解析式；
(3)求s关于m的函数关系式，并写出Q点的坐标．
29．(2019江苏淮安)如图，方格纸上每个小正方形的边长均为1个单位长度，点A、B都在格点上(两条网格线的交点叫格点)．
(1)将线段AB向上平移两个单位长度，点A的对应点为点A1，点B的对应点为点B1，请画出平移后的线段A1B1；
(2)将线段A1B1绕点A1按逆时针方向旋转90°，点B1的对应点为点B2，请画出旋转后的线段A1B2；
(3)连接AB2、BB2，求△ABB2的面积．
A．
1：2
B．
1：4
C．
1：5
D．
1：6
从分析问题的数量关系入手，适当设定未知数，把所研究的数学问题中已知量和未知量之间的数量关系，转化为方程或方程组的数学模型，从而使问题得到解决的思维方法
2、学会运用数形结合思想。
数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。
一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。
在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。
如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:
体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
专题32 中考几何平移类问题
1.平移的定义：平面图形的每个点沿着某一方向移动相同的距离，这样的图形运动称为平移.平移是由移动的方向和移动的距离所决定.平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。
2.平移的特点：经平移运动后的图形图形的位置发生变化, 形状和大小不变.
3.理解并掌握平移的三个特征：
(1)对应线段平行(或在一条直线上)且相等；对应角相等.
(2)对应点所连的线段平行(或在一条直线上)且相等.
(3)图形在平移后形状和大小都不变.
4.图形平移的画法：
(1)确定点；(2)定方向；(3)定距离。
【例题1】(2020•广东)在平面直角坐标系中，点(3，2)关于x轴对称的点的坐标为( )
A．(﹣3，2)B．(﹣2，3)C．(2，﹣3)D．(3，﹣2)
【对点练习】(2019湖南邵阳)一次函数y1=k1x+b1的图象l1如图所示，将直线l1向下平移若干个单位后得直线l2，l2的函数表达式为y2=k2x+b2．下列说法中错误的是( )
A．k1=k2 B．b1＜b2
C．b1＞b2 D．当x=5时，y1＞y2
【例题2】(2019桂林)如图，在平面直角坐标系中，反比例y＝(k＞0)的图象和△ABC都在第一象限内，AB＝AC＝，BC∥x轴，且BC＝4，点A的坐标为(3，5)．若将△ABC向下平移m个单位长度，A，C两点同时落在反比例函数图象上，则m的值为 ．
【对点练习】(2020枣庄模拟)已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A(0，3)、B(3，4)、C(2，2)(正方形网格中每个小正方形的边长是一个单位长度)．
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；
(2)以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是 ；
(3)△A2B2C2的面积是 平方单位．
【例题3】(2020•北京)在平面直角坐标系xOy中，一次函数y＝kx+b(k≠0)的图象由函数y＝x的图象平移得到，且经过点(1，2)．
(1)求这个一次函数的解析式；
(2)当x＞1时，对于x的每一个值，函数y＝mx(m≠0)的值大于一次函数y＝kx+b的值，直接写出m的取值范围．
一、选择题
1．(2020•菏泽)在平面直角坐标系中，将点P(﹣3，2)向右平移3个单位得到点P'，则点P'关于x轴的对称点的坐标为( )
A．(0，﹣2)B．(0，2)C．(﹣6，2)D．(﹣6，﹣2)
2.(2019哈尔滨)将抛物线向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线
为( )
A． B．
C． D．
3．(2019海南)如图，在平面直角坐标系中，已知点A(2，1)，点B(3，﹣1)，平移线段AB，使点A落在点A1(﹣2，2)处，则点B的对应点B1的坐标为( )
A．(﹣1，﹣1)B．(1，0)C．(﹣1，0)D．(3，0)
4．(2019广西梧州)直线y＝3x+1向下平移2个单位，所得直线的解析式是( )
A．y＝3x+3B．y＝3x﹣2C．y＝3x+2D．y＝3x﹣1
5．(2019广西百色)抛物线y＝x2+6x+7可由抛物线y＝x2如何平移得到的( )
A．先向左平移3个单位，再向下平移2个单位
B．先向左平移6个单位，再向上平移7个单位
C．先向上平移2个单位，再向左平移3个单位
D．先回右平移3个单位，再向上平移2个单位
6．(2020济南模拟)如图，在平面直角坐标系中，△ABC的顶点都在方格纸的格点上，如果将△ABC先向右平移4个单位长度，在向下平移1个单位长度，得到△A1B1C1，那么点A的对应点A1的坐标为( )
A．(4，3)B．(2，4)C．(3，1)D．(2，5)
7.将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式
为( )
A．y=(x﹣1)2+4B．y=(x﹣4)2+4C．y=(x+2)2+6D．y=(x﹣4)2+6
8．(2020咸宁模拟)如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为( )
9.如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为( )
A．48B．96C．84D．42
10.某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是( )
A．甲种方案所用铁丝最长B．乙种方案所用铁丝最长
C．丙种方案所用铁丝最长D．三种方案所用铁丝一样长
二、填空题
11．(2020•武威)如图，在平面直角坐标系中，△OAB的顶点A，B的坐标分别为(3，3)，(4，0)．把△OAB沿x轴向右平移得到△CDE，如果点D的坐标为(6，3)，则点E的坐标为 ．
12．(2020枣庄模拟)如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为 ．
13．(2020咸宁模拟)如图，在平面直角坐标系中，点A的坐标为(0，6)，将△OAB沿x轴向左平移得到△O′A′B′，点A的对应点A′落在直线y=﹣x上，则点B与其对应点B′间的距离为 ．
14．(2020岳阳模拟)如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论正确的是 ．(写出所有正确结论的序号)
①b＞0
②a﹣b+c＜0
③阴影部分的面积为4
④若c=﹣1，则b2=4a．
15.如图所示，一座楼房的楼梯，高1米，水平距离是2.8米，如果要在台阶上铺一种地毯，那么至少要买这种地毯________米．
16.如图，是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片，经测得FG＝9cm，则这个剪出的图形的周长是________cm．
17．如图，若△DEF是由△ABC经过平移后得到的，则平移的距离是_____．
18．(2019江苏徐州)已知二次函数的图象经过点P(2，2)，顶点为O(0，0)将该图象向右平移，当它再次经过点P时，所得抛物线的函数表达式为 ．
三、解答题
19．(2020•安顺)如图，一次函数y＝x+1的图象与反比例函数y=kx的图象相交，其中一个交点的横坐标
是2．
(1)求反比例函数的表达式；
(2)将一次函数y＝x+1的图象向下平移2个单位，求平移后的图象与反比例函数y=kx图象的交点坐标；
(3)直接写出一个一次函数，使其过点(0，5)，且与反比例函数y=kx的图象没有公共点．
20．(2020齐齐哈尔模拟)如图，在边上为1个单位长度的小正方形网格中：
(1)画出△ABC向上平移6个单位长度，再向右平移5个单位长度后的△A1B1C1．
(2)以点B为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2．
(3)求△CC1C2的面积．
21.(2020浙江宁波模拟)已知抛物线，其中是常数
(1)求证：不论为何值，该抛物线与轴一定有两个公共点；
(2)若该抛物线的对称轴为直线，
①求该抛物线的函数解析式；
②把该抛物线沿轴向上平移多少个单位长度后，得到的抛物线与轴只有一个公共点？
22.如图，在一块长为20m，宽为14m的草地上有一条宽为2m的曲折小路，你能运用你学的知识求出这块草地的绿地面积吗？
23．如图所示，将△ABC平移，可以得到△DEF，点B的对应点为点E，请画出点A的对应点D、点C的对应点F的位置，并作出△DEF．
24．如图，将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF，则四边形ABFD的周长?
25．如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．求证：BE=DG
26.如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A(﹣1，3)，B(﹣4，0)，C(0，0)。画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1。
27.如图，在一块长为20m，宽为14m的草地上有一条宽为2m的曲折小路，你能运用你学的知识求出这块草地的绿地面积吗？
28．(2019宁夏)将直角三角板ABC按如图1放置，直角顶点C与坐标原点重合，直角边AC、BC分别与x轴和y轴重合，其中∠ABC＝30°．将此三角板沿y轴向下平移，当点B平移到原点O时运动停止．设平移的距离为m，平移过程中三角板落在第一象限部分的面积为s，s关于m的函数图象(如图2所示)与m轴相交于点P(，0)，与s轴相交于点Q．
(1)试确定三角板ABC的面积；
(2)求平移前AB边所在直线的解析式；
(3)求s关于m的函数关系式，并写出Q点的坐标．
29．(2019江苏淮安)如图，方格纸上每个小正方形的边长均为1个单位长度，点A、B都在格点上(两条网格线的交点叫格点)．
(1)将线段AB向上平移两个单位长度，点A的对应点为点A1，点B的对应点为点B1，请画出平移后的线段A1B1；
(2)将线段A1B1绕点A1按逆时针方向旋转90°，点B1的对应点为点B2，请画出旋转后的线段A1B2；
(3)连接AB2、BB2，求△ABB2的面积．
A．
1：2
B．
1：4
C．
1：5
D．
1：6
相关试卷
(通用版)中考数学总复习考点32 中考几何平移类问题（含解析）： 这是一份(通用版)中考数学总复习考点32 中考几何平移类问题（含解析），共26页。试卷主要包含了平移的定义，平移的特点，理解并掌握平移的三个特征，图形平移的画法等内容，欢迎下载使用。
中考数学专题复习 专题39 中考函数综合类问题： 这是一份中考数学专题复习 专题39 中考函数综合类问题，文件包含中考数学专题复习专题39中考函数综合类问题教师版含解析docx、中考数学专题复习专题39中考函数综合类问题学生版docx等2份试卷配套教学资源，其中试卷共47页， 欢迎下载使用。
中考数学专题复习 专题34 中考几何旋转类问题： 这是一份中考数学专题复习 专题34 中考几何旋转类问题，文件包含中考数学专题复习专题34中考几何旋转类问题教师版含解析docx、中考数学专题复习专题34中考几何旋转类问题学生版docx等2份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。
