






- 中考数学专项突破之函数的实际应用 课件 课件 0 次下载
- 中考数学专项突破之函数的图象与性质 课件 课件 0 次下载
- 中考数学专项突破之函数图象的判断与分析 课件 课件 0 次下载
- 中考数学专项突破之实践操作与探究 课件 课件 0 次下载
- 中考数学专项突破之数学思想与方法 课件 课件 0 次下载
中考数学专项突破之规律与猜想 课件
展开通常按照一定的顺序给定一列数或代数式,要求我们根据这些已知的量,猜想其中蕴含的规律.表示或揭示这些规律时,常常包含着这个数字或代数式的序列号. 一般解法是先写出数式的基本结构,然后通过横比(比较同一等式中不同部分的数量关系)或纵比(比较不同等式间相同位置的数量关系)找出各部分的特征,改写成要求的格式.
1.将所给的每个数据化为有规律的代数式; 2.按规律顺序排列这些式子; 3.将发现的规律用代数式表示出来; 4.用题中所给数据验证规律的正确性. 我们需要熟记的数字规律有: (1)自然数列规律:0,1,2,3,…,n(n≥0). (2)正整数列规律:1,2,3,…,n-1,n(n≥1).
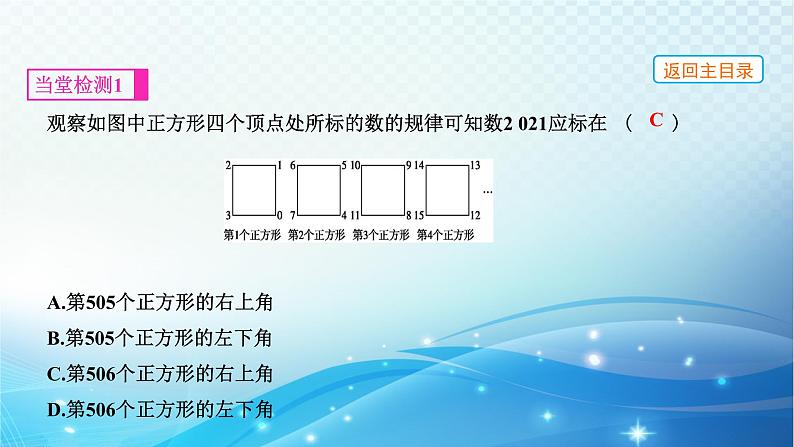
观察如图中正方形四个顶点处所标的数的规律可知数2 021应标在( ) A.第505个正方形的右上角 B.第505个正方形的左下角 C.第506个正方形的右上角 D.第506个正方形的左下角
解析:观察题中给出的几个正方形可知,每个正方形对应4个数,第一个正方形中最小的数是0,0在右下角,其余数按逆时针由小到大排列,2 021÷4=505……1,第504个正方形中最大的数是2 015,第505个正方形中最大的数是2 019,第506个正方形中最小的数是2 020,2 021位于正方形的右上角.
算式规律的问题,即用运算符号将按一定规律排列的数字连接起来的等式或不等式问题,这类问题往往给出了一组变化的等式或不等式,要求通过观察、分析,猜想出序号与各个算式之间蕴含的规律. 1.观察构成每个等式或不等式的数据的变化规律,并用关于序号的代数式表示出来; 2.按规律顺序将这些代数式排列出来; 3.用题中所给式子验证规律的正确性.
观察等式两边的数的特点,用n表示其规律.
(2020·石家庄新华区一模)(1)观察下列算式,并完成填空:1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;
……1+3+5+…+(2n-1)= .(n是正整数) 分析:观察算式规律,1+3+5+…+(2n-1)=n2. 解析:观察算式规律,1+3+5+…+(2n-1)=n2,故答案为n2.(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;……以此递推.
①第3层中分别含有 块正方形和 块正三角形地板砖; ②第n层中含有 块正三角形地板砖(用含n的代数式表示). 分析:①第一层有6块正方形和6块正三角形地板砖,第二层有6块正方形和6+12=18块正三角形地板砖,第三层有6块正方形和18+12=30块正三角形地板砖;②第一层有6=6×1=6×(2×1-1)块正三角形地板砖,第二层有18=6×3=6×(2×2-1)块正三角形地板砖,第三层有30=6×5=6×(2×3-1)块正三角形地板砖,第n层有6(2n-1)块正三角形地板砖.
6(2n-1)/12n-6
解析:①∵第一层包括6块正方形和6块正三角形地板砖,第二层包括6块正方形和6+12=18块正三角形地板砖,∴第三层包括6块正方形和18+12=30块正三角形地板砖.故答案为6,30.②∵第一层有6=6×1=6×(2×1-1)块正三角形地板砖,第二层有18=6×3=6×(2×2-1)块正三角形地板砖,第三层有30=6×5=6×(2×3-1)块正三角形地板砖,∴第n层有6(2n-1)块正三角形地板砖.故答案为6(2n-1)或12n-6.
理由如下:∵150÷6=25(层),∴150块正方形地板砖可以铺设这样的图案25层.∵铺设n层需要正三角形地板砖的数量为6[1+3+5+…+(2n-1)]=6n2,∴6n2=420,n2=70,n=70.又∵8<70<9,即8
(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:①52× = ×25;② ×396=693× ;解:①∵5+2=7,∴左边的三位数是275,右边的三位数是572.∴52×275=572×25.②∵左边的三位数是396,∴左边的两位数是63,右边的两位数是36,63×396=693×36. 故答案为①275,572;②63,36.
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并证明.解:∵左边两位数的十位数字为a,个位数字为b,∴左边的两位数是10a+b,三位数是100b+10(a+b)+a,右边的两位数是10b+a,三位数是100a+10(a+b)+b,∴一般规律的式子(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a). 证明:左边=(10a+b)×[100b+10(a+b)+a]=(10a+b)(100b+10a+10b+a)=(10a+b)(110b+11a)=11(10a+b)(10b+a),
右边=[100a+10(a+b)+b]×(10b+a) =(100a+10a+10b+b)(10b+a) =(110a+11b)(10b+a)=11(10a+b)(10b+a),左边=右边,∴“数字对称等式”一般规律的式子为(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).
根据图形找规律的题目在中考中也是常考类型,大致有两种题型:一种是数形规律,即根据一组图形的排列探究图形所反映的规律;另外一种是图形的运动规律,即根据一组相关图案的变化,从中总结图形的变化所反映的规律.在中考中以图形为载体的数字规律最为常见. 数形规律题的解题关键是通过图形寻找数量关系,并用代数式表示规律,最后进行验证;图形运动规律题的解题关键是抓住图形的本质特征,并仿照原题进行证明.
在图形变化规律题中探索递推规律时,往往从少到多,从简单到复杂,要通过比较和分析,找出每次变化过程中都具有规律性的东西和不易看清的图形变化部分.
问题提出:用若干相同的一个单位长度的细直木棒,按照下图方式搭建一个长方体框架,探究所用木棒条数的规律.
问题探究: 我们先从简单的问题开始探究,从中找出解决问题的方法. 探究一 用若干木棒来搭建横长是m,纵长是n的矩形框架(m,n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条; 如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条; 如图③,当m=2,n=2时,横放木棒为2×(2+1)条,纵放木棒为(2+1)×2条,共需12条; 如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条; 如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条. 问题(一):当m=4,n=2时,共需木棒 条. 分析:由图①②③④⑤探索横放条数+纵放条数=总条数,其中横放条数=横长m×
(纵长n+1),纵放条数=(横长m+1)×纵长n,故当m=4,n=2时,共需木4×(2+1)+(4+1)×2=12+10=22条.解析:当m=4,n=2时,共需木棒4×(2+1)+(4+1)×2=12+10=22条. 问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为 条,纵放的木棒为 条. 分析:当矩形框架横长是m,纵长是n时,横放的木棒为m(n+1)条,纵放的木棒为n(m+1)条.解析:当矩形框架横长是m,纵长是n时,横放的木棒为m(n+1)条,纵放的木棒为n(m+1)条.
探究二 用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m,n,s是正整数),需要木棒的条数. 如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条; 如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条; 如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条. 实际应用:现在按探究二的搭建方式搭建一个纵长是2,高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 . 拓展应用:若按照如图方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条. 分析:问题(三):由图⑥⑦⑧探索发现:横放与纵放木棒条数之和=
[m(n+1)+(m+1) n](s+1)
s(m+1)(n+1)
[m(n+1)+(m+1)n](s+1),竖放木棒条数= s (m+1)(n+1); 实际应用:按探究二的搭建方式搭建一个纵长是2,高是4的长方体框架,总共使用了170条木棒,设这个长方体框架的横长是x,根据发现的规律得[2(x+1)+x(2+1)](4+1)+4(2+1)(x+1)=170,解得x=4; 拓展应用:若按照如图方式搭建一个底面边长是10,高是5的正三棱柱框架,每层三角形从左到右底的个数=(1+2+3+4+5+…+10),有两个腰,腰的总个数=2(1+2+3+4+5+…+10),共有6层,则需要横放与纵放木棒条数之和=6×(1+2)×(1+2+3+4+5+…+10)=990条,竖放木棒条数=5×(1+2+3+4+5+…+10+11)=330条,故总共需要木棒990+330=1 320条.解析:问题(三):由图⑥⑦⑧探索发现:横放与纵放木棒条数之和=
[m(n+1)+(m+1) n](s+1),竖放木棒条数= s (m+1)(n+1);实际应用:设这个长方体框架的横长是x,根据发现的规律得[2(x+1)+x(2+1)](4+1)+4(2+1)(x+1)=170,解得x=4;拓展应用:若按照如图方式搭建一个底面边长是10,高是5的正三棱柱框架,每层三角形从左到右底的个数=(1+2+3+4+5+…+10),有两个腰,腰的总个数=2(1+2+3+4+5+…+10),共有6层,则需要横放与纵放木棒条数之和=6×(1+2)×(1+2+3+4+5+…+10)=990条,竖放木棒条数=5×(1+2+3+4+5+…+10+11)=330条,故总共需要木棒990+330=1 320条.【高分点拨】先由图形的特点总结出其数字特征,再总结归纳数字的变化特征(也可借助图形的变化规律找),找到规律性的算式,最后进行检验.
“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法. 例如,图①有6个点,图②有12个点,图③有18个点,…,按此规律,求图⑩、图 有多少个点. 我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图1,2,3),这样图①中黑点个数是6×1=6个,图②中黑点个数是6×2=12个,图③中黑点个数是6×3=18个,…,所以容易求出图⑩、图 中黑点个数分别是 、 . 解:图⑩中黑点个数是6×10=60个;图 中黑点个数是6n个.故答案为60个,6n个. 请你参考以上“分块计数法”,先将下面的点阵进行分块,再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈; 解:如图所示,第1个点阵中有1个圆圈,第2个点阵中有2×3+1=7个圆圈,第3个点阵中有3×6+1=19个圆圈,第4个点阵中有4×9+1=37个圆圈,第5个点阵中有5×12+1=61个圆圈,……第n个点阵中有n×3(n-1)+1=(3n2-3n+1)个圆圈,故答案为61,3n2-3n+1.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
解:3n2-3n+1=271,n2-n-90=0,(n-10)(n+9)=0,n1=10,n2= -9(舍去),∴小圆圈的个数会等于271,它是第10个点阵.
坐标变化规律型的题目主要考查了点的坐标规律,培养学生的观察和归纳能力,从所给的数据和图形中寻求规律进行解题是解答本类问题的关键. 此类题型主要考查点的坐标变化规律,解决此类问题的关键是从点的变化中发现横坐标、纵坐标的变化规律.
坐标变化规律的发掘,要充分和图形联系起来,将图形、坐标和坐标对应的序号综合考虑;坐标中横、纵坐标的变化规律可能不同,要分别考虑.
在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按下图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5→…”的路线运动,设第n秒运动到点Pn(n为正整数),则点P2 019的坐标是 .
高效测评1.如图,第①幅“龟图”中有5个“ ”,第②幅“龟图”中有7个“ ”,第③幅“龟图”中有11个“ ”,若第 幅“龟图”中有61个“ ”,则n的值为( ) A.7 B.8 C.9 D.3 665
解析:第一个图形有5个“ ”,第二个图形有2×1+5=7个“ ”,第三个图形有3×2+5=11个“ ”,第四个图形有4×3+5=17个“ ”, 由此可得第n个图形有[n(n-1)+5]个“ ”,则可得方程:[n(n-1)+5]=61, 解得n1=8,n2=-7(舍去).故选B.
2.下列图形都是由同样大小的地砖按照一定规律所组成的,其中第①个图形中有4块地砖,第②个图形中有9块地砖,第③个图形中有16块地砖,…,按此规律排列下去,第9个图形中地砖的块数为( ) A.81 B.99 C.100 D.121
解析:第①个图形中有22=4块地砖,第②个图形中有32=9块地砖,第③个图形中有42=16块地砖,……第n个图形中有(n+1)2块地砖,第9个图形中地砖的块数为102=100,故选C.
3.观察算式:31+2=5;32+2=11;33+2=29;34+2=83;35+2=245;36+2=731;…;则32 021+2 021的个位数字是 . 解析:∵31+2=5;32+2=11;33+2=29;34+2=83;35+2=245;36+2=731;…;∴结果的尾数5,1,9,3一循环.∵2 021÷4=505……1,∴32 021+2的尾数与31+2尾数相同,为5,∴32 021+2 021=32 021+2+2 019的个位数字是5+9-10=4.
5.每一层三角形的个数与层数的关系如图所示,则第2 021层的三角形个为 . 解析:∵第一层有1个,即1=2×1-1;第二层有3个,即3=2×2-1;第三层有5个,即5=2×3-1;第四层有7个,即7=2×4-1;……以此类推,可得第n层有(2n-1)个三角形,当n=2 021时,三角形的个数为2×2 021-1=4 041.
8.如图,过点A1(1,0)作x轴的垂线,交直线 y=2x 于点B1,点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线 y=2x 于点B2;点A3与点O关于直线A2B2对称;过点A3作x轴的垂线,交直线y=2x于点B3;…;按此规律作下去,则:(1)点B4的坐标为 ; (2)点Bn的坐标为 . 解析:∵点A1坐标为(1,0),∴OA1=1,过点A1作x轴的垂线交直线于点B1,可知点B1的坐标为(1,2).
∵点A2与点O关于直线A1B1对称,∴OA1=A1A2=1,∴OA2=1+1=2,∴点A2的坐标为(2,0),B2的坐标为(2,4).∵点A3与点O关于直线A2B2对称,故点A3的坐标为(4,0),B3的坐标为(4,8),以此类推便可求出点An的坐标为(2n-1,0),点Bn的坐标为(2n-1,2n).所以点A4的坐标为(8,0),点B4的坐标为(8,16),故答案为(8,16),(2n-1,2n).
9.如图,已知直线l:y= -x+4,在直线l上取点B1,过B1分别向x轴、y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴、A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An-1AnBnCn,则A3的坐标为 ,B5的坐标为 . 解析:设直线l交y轴于点E,交x轴于点F.当x=0时,y=4,当y=0时,-x+4=0,x=4,∴OE=OF=4,∴△EOF是等腰直角三角形,∴∠C1EF=45°,
10.将从1开始的连续自然数按下表规律排列:规定位于第m行、第n列的自然数记为(m,n).例如:自然数8记为(2,1),自然数10记为(3,2),自然数15记为(4,2),…,按此规律,自然数2 021记为 .
解析:依题意可知,每4个自然数排一行,其中奇数行的数字从左往右依次增大,偶数行的数字从左往右依次减少,如图所示:∵2 021÷4=505……1,∴自然数2 021位于第506行、第4列,记为(506,4).
11.将从1开始的连续自然数按如下规律排列: 则2 021在第 行.
解析:通过观察,得知第1行有一个数,可表示为12;前2行一共有1+3=4个数,可表示为22;前3行一共有1+3+5=9个数,可表示为32;前4行一共有1+3+5+7=16个数,可表示为42;前5行一共有1+3+5+7+9=25个数,可表示为52;……前n行一共有1+3+5+…+(2n-1)个数,可表示为n2,∵前44行一共有442=1 936个数,前45行一共有452=2 025人数,∴2 021在第45行.
(2)请写出OA,OB,OD三条射线上数字的排列规律;解:根据已知总结排列如下:射线OA上的数字排列规律:6n-5(n为正整数);射线OB上的数字排列规律:6n-4(n为正整数);射线OC上的数字排列规律:6n-3(n为正整数);射线OD上的数字排列规律:6n-2(n为正整数);射线OE上的数字排列规律:6n-1 (n为正整数);射线OF上的数字排列规律:6n(n为正整数). (3)“2 021”在哪条射线上?解:∵在六条射线上的数字规律中,只有6n-1=2 021有整数解,解得n=337,∴“2 021”在射线OE上.
12.如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….(1)“17”在射线 上;解:根据图形总结数字的排列规律如下:射线OA:1,7,13,19,…;射线OB:2,8,14,20,…;射线OC:3,9,15,21,…;射线OD:4,10,16,22,…;射线OE:5,11,17,23,…;射线OF:6,12,18,24,…;故“17”在射线OE上.
13.阅读下列材料:小明为了计算1+2+22+…+22 020+22 021的值,采用以下方法:设S=1+2+22+…+22 020+22 021,①则2S=2+22+…+22 021+22 022,②②-①,得2S-S=S=22 022-1,∴S=1+2+22+…+22 020+22 021=22 022-1.请仿照小明的方法解决以下问题:(1)1+2+22+…+29= ; 解:设S=1+2+22+…+29,① 则2S=2+22+…+210,②②-①,得2S-S=S=210-1,∴S=1+2+22+…+29=210-1,故答案为210-1.
中考数学专项突破之阅读理解 课件: 这是一份中考数学专项突破之阅读理解 课件,共39页。PPT课件主要包含了答案C,高效测评等内容,欢迎下载使用。
中考数学专项突破之圆的综合题 课件: 这是一份中考数学专项突破之圆的综合题 课件,共60页。PPT课件主要包含了高效测评等内容,欢迎下载使用。
中考数学专项突破之数学思想与方法 课件: 这是一份中考数学专项突破之数学思想与方法 课件,共47页。PPT课件主要包含了返回主目录,≤k≤275等内容,欢迎下载使用。












