
四川省巴中市巴州区2023年八年级下学期期中数学试卷【含答案】
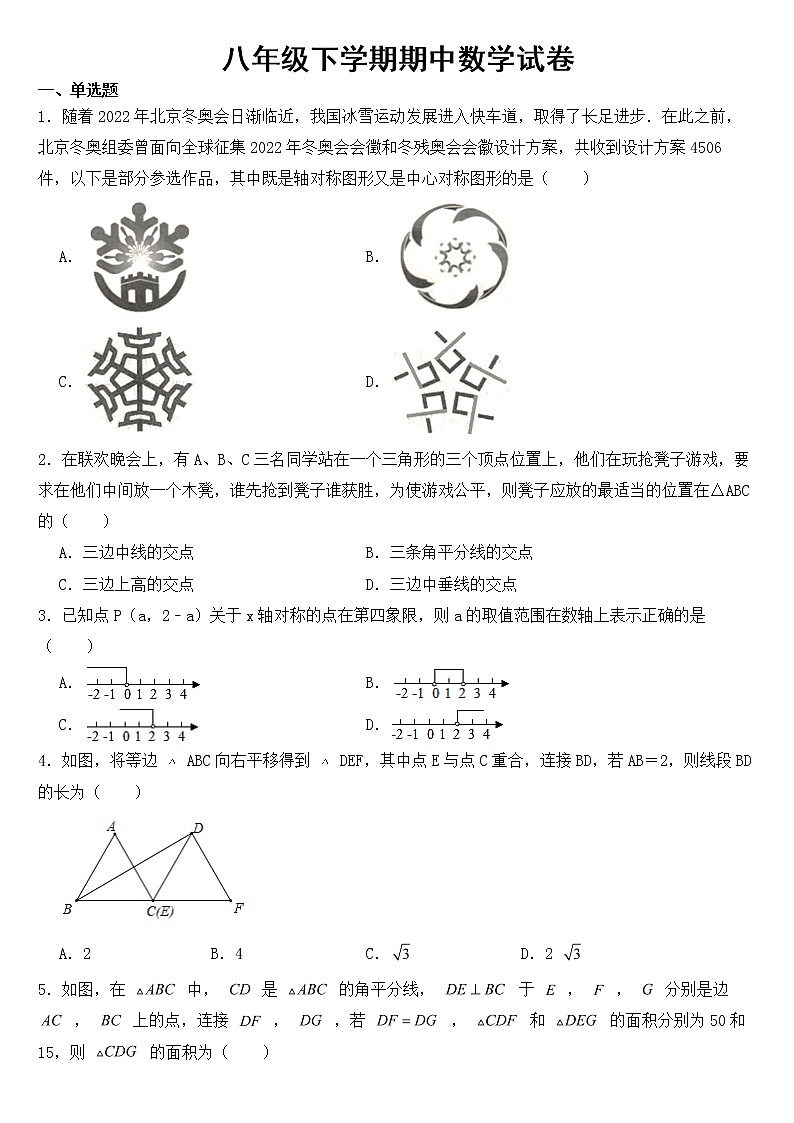
展开1.随着2022年北京冬奥会日渐临近,我国冰雪运动发展进入快车道,取得了长足进步.在此之前,北京冬奥组委曾面向全球征集2022年冬奥会会徵和冬残奥会会徽设计方案,共收到设计方案4506件,以下是部分参选作品,其中既是轴对称图形又是中心对称图形的是( )
A.B.
C.D.
2.在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )
A.三边中线的交点B.三条角平分线的交点
C.三边上高的交点D.三边中垂线的交点
3.已知点P(a,2﹣a)关于x轴对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.B.
C.D.
4.如图,将等边 ABC向右平移得到 DEF,其中点E与点C重合,连接BD,若AB=2,则线段BD的长为( )
A.2B.4C.D.2
5.如图,在 中, 是 的角平分线, 于 , , 分别是边 , 上的点,连接 , ,若 , 和 的面积分别为50和15,则 的面积为( )
A.30B.25C.20D.15
6.若m>n,下列不等式不一定成立的是( )
A.m+2>n+2B.2m>2nC. > D.m2>n2
7.如图,在 ABC中,∠ACB=90°,分别以A,B为圆心,以大于 AB的长为半径作弧,两弧分别交于M,N两点,作直线MN交AB于点D,交AC于点F,连接BF,下列结论不一定成立的是( )
A.BF=AFB.∠CBF=90°﹣2∠A
C.∠ABF=∠FBCD. ADF≌ BDF
8.已知在等腰三角形ABC中,D为BC的中点AD=12,BD=5,AB=13,点P为AD边上的动点,点E为AB边上的动点,则PE+PB的最小值是( )
A.10B.12C.D.
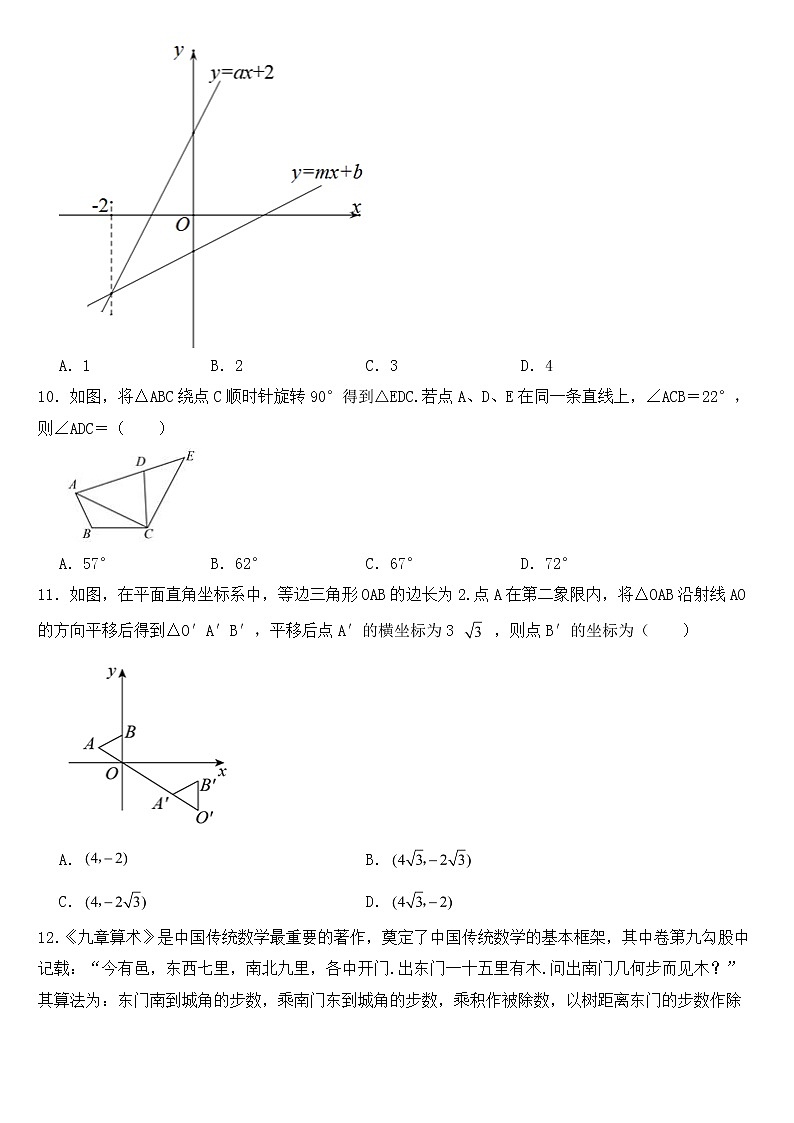
9.如图,已知直线y=ax+2与直线y=mx+b的交点的横坐标是﹣2.根据图象有下列四个结论:①a>0;②b<0;③方程ax+2=mx+b的解是x=﹣2;④不等式ax﹣b>mx﹣2的解集是x>﹣2.其中正确的结论个数是( )
A.1B.2C.3D.4
10.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,∠ACB=22°,则∠ADC=( )
A.57°B.62°C.67°D.72°
11.如图,在平面直角坐标系中,等边三角形OAB的边长为2.点A在第二象限内,将△OAB沿射线AO的方向平移后得到△O′A′B′,平移后点A′的横坐标为3 ,则点B′的坐标为( )
A.B.
C.D.
12.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木?”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门 里见到树,则 .若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城周长的最小值为( )(注:1里=300步,且两个正数的和大于等于其积开方的两倍,当两数相等时取等号).
A. 里B. 里C. 里D. 里
二、填空题
13.用反证法证明命题“三角形中至少有两个锐角”,第一步应假设 .
14.若关于x的不等式x﹣m≥﹣1的解集如图所示,则m等于 .
15.如图,在等腰三角形ABC中, ,BD是AC边上的中线,已知 的周长是36, 的周长比 的周长多6,则AB的长是 .
16.已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),甲、乙的面积分别为S1,S2.
(1)S1与S2的大小关系为:S1 S2;(用“>”、“<”、“=”填空)
(2)若满足条件21<n≤|S1﹣S2|的整数n有且只有4个,则m的值是 .
17.如图,在 中, 是 的平分线,若 ,则 .
18.如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是 (写出正确结论的序号).
三、解答题
19.解不等式:
(1) .
(2)已知 ,化简: .
(3)求不等式组 的整数解.
20.已知关于x、y的方程组 中,x为非负数、y为负数.
(1)试求m的取值范围;
(2)当m取何整数时,不等式3mx+2x>3m+2的解集为x<1.
21.如图,在 中, , , 是 的垂直平分线.
(1)求证: 是等腰三角形.
(2)若 的周长是 , ,求 的周长.(用含 , 的代数式表示)
22.如图,平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)在平面直角坐标系中画出与△ABC关于点P(1,0)成中心对称的△A'B'C',并分别写出点A',B',C'的坐标;
(2)如果点M(a,b)是△ABC边上(不与A,B,C重合)任意一点,请写出在△A'B'C'上与点M对应的点M'的坐标.
23.阅读下列内容,设a, b, c是一个三角形的三条边的长,且a是最长边,我们可以利用a, b, c三边长间的关系来判断这个三角形的形状;
①若 则该三角形是直角三角形②若 ,则该三角形是钝角三角形;③ ;则该三角形是锐角三角形
例如一个三角形的三边长分别是4,5,6则最长边是6, ,故由上面③可知该三角形是锐角三角形,请解答以下问题
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是 三角形
(2)若一个三角形的三条边长分别是3,4,x且这个三角形是直角三角形则x的值为
(3)若一个三角形的三条边长分别为 ,mn, ,请判断这个三角形的形状,并写出你的判断过程.
24.一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手,某公司用甲,乙两种货车向武汉运送爱心物资.两次满载的运输情况如表:
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)由于疫情的持续,该公司安排甲乙货车共10辆进行第三次物资的运送,运送的物资不少于48.4吨,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
25.如图,在平面直角坐标系中,直线y=kx过点B(m,6),过点B分别作x轴和y轴的垂线,垂足分别为点A,C,∠AOB=30°.动点P从点O出发,以每秒2个单位长度的速度向点B运动,动点Q从点B出发.以每秒 个单位长度的速度向点C运动.点P,Q同时开始运动,当点P到达点B时,点P,Q同时停止运动,设运动时间为t秒.
(1)求m与k的值;
(2)设△PQB的面积为S,求S与t的关系式;
(3)若以点P,Q,B为顶点的三角形是等腰三角形,请求出t的值.(温擎提示:在直角三角形中,30°的角所对的直角边等于斜边的一半)
1.C
2.D
3.B
4.D
5.C
6.D
7.C
8.D
9.D
10.C
11.D
12.D
13.同一三角形中最多有一个锐角
14.3
15.14
16.(1)>
(2)13
17.
18.①②④
19.(1)解:
去分母,得:
去括号,得:
移项、合并同列项,得:
系数化为1,得: ;
(2)解:解不等式 ,
得: .
∴ , ,
∴ ;
(3)解: ,
解不等式①,得: ,
解不等式②,得: ,
∴该不等式组的解集为 ,
∴该不等式组的整数解为:-1,0,1.
20.(1)解: ,
①+②得:2x=18﹣4m,x=9﹣2m,
①﹣②得:﹣2y=4+2m,y=﹣2﹣m,
∵x为非负数、y为负数,
∴ ,解得:﹣2
(3m+2)x>3m+2,
∵不等式3mx+2x>3m+2的解为x<1,
∴3m+2<0,
∴m<﹣ ,
由(1)得:﹣2
∴m=﹣1;
即当m=﹣1时,不等式3mx+2x>3m+2的解为x<1.
21.(1)证明:∵ ,
∴
∵ 是 的垂直平分线
∴
∴
∵ 是 的外角
∴
∴
∴
∴ 是等腰三角形;
(2)解:∵ , 的周长是
∴
∵
∴
∴ 的周长 .
22.(1)解:△A'B'C'如图所示,A′(3,2),B′(4,4),C′(6,1);
(2)解:设M′(m,n),
则有 , ,
∴m=2−a,n=−b,
∴M′(2−a,−b).
23.(1)钝角
(2)5或
(3)解:若一个三角形的三条边长分别是 ,mn, ,这个三角形是直角三角形;理由如下:
∵ > , ≥mn, ;
∴这个三角形是直角三角形.
24.(1)解:设甲、乙两种货车每次满载分别能运输x吨和y吨物资,
根据题意,得 ,
解得: ,
∴甲、乙两种货车每次满载分别能运输5吨和4吨物资,
答:甲、乙两种货车每次满载分别能运输5吨和4吨物资;
(2)解:设安排甲货车z辆,乙货车(10-z)辆,总运费为w元,根据题意得,
w=500z+300(10-z)=200z+3000,
∵200>0,
∴w随z的增大而增大,
∵运送的物资不少于48.4吨,
∴ ,
∴ ,
又∵z是整数,
∴当z=9时,w的值最小为w=200×9+3000=4800,
答:该公司应安排甲种货车9辆,乙种货车1辆最节省费用.
25.(1)解: ,
,
, ,
, ,
, ,
,即 , ,
直线 过点 , ,
;
(2)解:如图1,过点 作 于点 ,
, ,则 ,
,
在 中, ,
;
(3)解:分三种情况:
①当 时, ,
解得 ;
②当 时,如图2,过点 作 于点 ,
,
,
解得 ;
③当 时,如图3,过点 作 于点 ,
则 ,
,
解得 ;
综上所述,当 为等腰三角形时, 的值为 或4或 .
甲种货车辆数
乙种货车辆数
合计运物资吨数
第一次
3
4
31
第二次
2
6
34
2022-2023学年四川省巴中市巴州区九年级(上)期末数学试卷(含解析): 这是一份2022-2023学年四川省巴中市巴州区九年级(上)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省巴中市巴州区2023-2024学年八年级上学期期中数学试卷: 这是一份四川省巴中市巴州区2023-2024学年八年级上学期期中数学试卷,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省巴中市巴州区2023-2024学年 八年级上学期数学期中测试: 这是一份四川省巴中市巴州区2023-2024学年 八年级上学期数学期中测试,文件包含湖南师大附中数学附中3次pdf、湖南师大附中数学答案附中3次pdf等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。













