






高中数学高考通用版2020版高考数学大一轮复习第9讲对数与对数函数课件文新人教A版
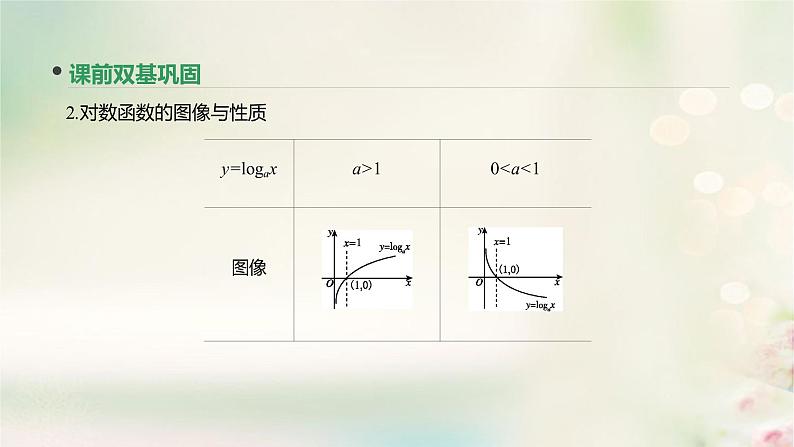
展开课前双基巩固│课堂考点探究│教师备用例题logaN=x对数01.对数NlogaM+logaNlogaM-logaNnlogaM(续表)2.对数函数的图像与性质3.集合的基本运算3.集合的基本运算(1,0)R(0,+∞)01y0y0增减(续表)y=logax(a>0且a≠1)y=x题组一 常识题题组二 常错题◆索引:对数的性质及其运算掌握不到位致错;忽略真数大于零致错;对数函数的性质不能充分运用致错;忽略对底数的讨论致误.探究点一 对数式的化简与求值[总结反思] (1)对数运算法则是在化为同底的情况下运用的,因此经常会用到换底公式及其推论.在对含有字母的对数式进行化简时,必须保证恒等变形.(2)利用对数运算法则,在真数的积、商、幂与对数的和、差、倍之间进行转化.探究点二 对数函数的图像及应用[总结反思] (1)在研究对数型函数的图像时一定要注意其定义域,注意根据基本的对数函数图像作出经过平移、对称变换得到的函数的图像;(2)一些对数型方程(不等式)问题常转化为相应的函数图像问题,利用数形结合求解.微点1 比较大小微点2 解简单对数不等式[总结反思] 对数不等式(组)的求解常利用对数函数的单调性,在对数的底数不确定的情况下,要注意分类讨论.微点3 对数函数性质的综合问题[思路点拨] (1)将问题转化为3-ax>0在[0,2]上恒成立求解;(2)由复合函数的单调性求出f(x)在区间[1,2]上的最大值,再根据最大值为1,得到关于a的方程.[总结反思] 利用对数函数的性质,求与对数函数有关的函数值域和复合函数的单调性问题,必须弄清三方面的问题:一是定义域,所有问题都必须在定义域内讨论;二是底数与1的大小关系;三是复合函数的构成,即它是由哪些基本初等函数复合而成的.应用演练【备选理由】 这里选用的四道例题,比前面的例题难度大一些,其目的是为了提升学生灵活运用函数的性质解题的能力.






