

高中数学高考卷02-2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版)
展开注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.测试范围:高中全部内容.
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合A={x|x2﹣2x﹣3<0},集合B={x|x<1},则A∩B等于( )
A.(1,3)B.(﹣∞,﹣1)
C.(﹣1,1)D.(﹣3,1)
【答案】C
【解析】A={x|x2﹣2x﹣3<0}={x|﹣1<x<3},集合B={x|x<1},
则A∩B={x|﹣1<x<1}=(﹣1,1),
故选:C.
2.若纯虚数z满足z(1﹣2i)=a+i,其中a∈R,i是虚数单位,则实数a的值等于( )
A.﹣2B.-12
C.2D.12
【答案】C
【解析】设z=bi(b≠0),
由z(1﹣2i)=a+i,得bi(1﹣2i)=a+i,
即2b+bi=a+i,
∴b=1,a=2.
故选:C.
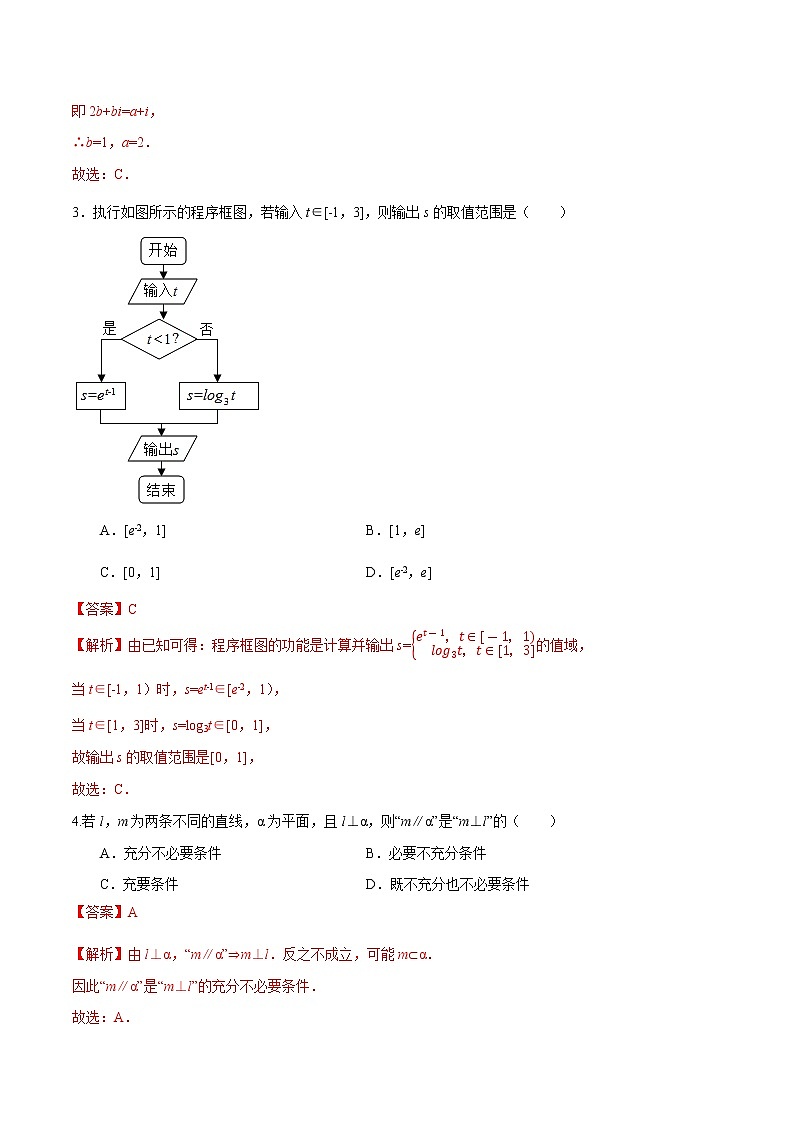
3.执行如图所示的程序框图,若输入t∈[﹣1,3],则输出s的取值范围是( )
A.[e﹣2,1]B.[1,e]
C.[0,1]D.[e﹣2,e]
【答案】C
【解析】由已知可得:程序框图的功能是计算并输出s=&et-1,t∈[-1,1)&lg3t,t∈[1,3]的值域,
当t∈[﹣1,1)时,s=et﹣1∈[e﹣2,1),
当t∈[1,3]时,s=lg3t∈[0,1],
故输出s的取值范围是[0,1],
故选:C.
4.若l,m为两条不同的直线,α为平面,且l⊥α,则“m∥α”是“m⊥l”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】A
【解析】由l⊥α,“m∥α”⇒m⊥l.反之不成立,可能m⊂α.
因此“m∥α”是“m⊥l”的充分不必要条件.
故选:A.
5.设x,y满足约束条件&x-y+1≥0&x+2y-2≥0&4x-y-8≤0,则z=|x+3y|的最大值为( )
A.15B.13
C.3D.2
【答案】A
【解析】由约束条件&x-y+1≥0&x+2y-2≥0&4x-y-8≤0作出可行域如图,
联立&x-y+1=0&4x-y-8=0,解得A(3,4),
由图可知,z=|x+3y|=x+3y,化为y=﹣x3+z3.
当直线y=﹣x3+z3过A时,直线在y轴上的截距最大,z有最大值为15.
故选:A.
6.已知三棱锥P﹣ABC所有顶点都在球O的球面上,底面△ABC是以C为直角顶点的直角三角形,AB=22,PA=PB=PC=3,则球O的表面积为( )
A.9πB.9π4
C.4πD.π
【答案】A
【解析】设AB中点为D,则D为△ABC的外心,因为PA=PB=PC=3,易证PD⊥面ABC,
,所以球心O在直线PD上,
又PA=3,AB=22,
算得PD=1,
设球半径为R,则△AOD中,
(R﹣1)2+2=R2,
可得:R=32.
则球O的表面积S=4πR2=9π,
故选:A.
7.定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),当x∈[0,1]时,f(x)=﹣2x+1,设函数g(x)=(12)|x﹣1|(﹣1<x<3),则函数f(x)与g(x)的图象所有交点的横坐标之和为( )
A.2B.4
C.6D.8
【答案】B
【解析】∵f(x+1)=﹣f(x),
∴f(x+2)=﹣f(x+1)=f(x),
∴f(x)的周期为2.
∴f(1﹣x)=f(x﹣1)=f(x+1),
故f(x)的图象关于直线x=1对称.
又g(x)=(12)|x﹣1|(﹣1<x<3)的图象关于直线x=1对称,
作出f(x)的函数图象如图所示:
由图象可知两函数图象在(﹣1,3)上共有4个交点,
∴所有交点的横坐标之和为1×2×2=4.
故选:B.
8.在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,BM→=2MA→,CN→=2NA→,则BC→⋅OM→的值为( )
A.﹣15B.﹣9
C.﹣6D.0
【答案】C
【解析】
解法Ⅰ,由题意,BM→=2MA→,CN→=2NA→,
∴BMMA=CNNA=2,∴BC∥MN,且BC=3MN,
又MN2=OM2+ON2﹣2OM•ON•cs120°=1+4﹣2×1×2×(﹣12)=7,
∴MN=7;
∴BC=37,
∴cs∠OMN=OM2+MN2-ON22OM⋅MN=1+7-42×1×7=27,
∴BC→•OM→=|BC→|×|OM→|cs(π﹣∠OMN)=37×1×(﹣27)=﹣6.
解题Ⅱ:不妨设四边形OMAN是平行四边形,
由OM=1,ON=2,∠MON=120°,BM→=2MA→,CN→=2NA→,
知BC→=AC→﹣AB→=3AN→﹣3AM→=﹣3OM→+3ON→,
∴BC→⋅OM→=(﹣3OM→+3ON→)•OM→
=﹣3OM→2+3ON→•OM→
=﹣3×12+3×2×1×cs120°
=﹣6.
故选:C.
9.若lg2,lg(2x+1),lg(2x+5)成等差数列,则x的值等于( )
A.1B.0或18
C.18D.lg23
【答案】D
【解析】由lg2,lg(2x+1),lg(2x+5)成等差数列,
得2lg(2x+1)=lg2+lg(2x+5),
∴lg(2x+1)2=lg2(2x+5),即(2x+1)2=2•2x+10,
整理得:(2x)2=9,即2x=3,
∴x=lg23.
故选:D.
10.△ABC的内角A,B,C的对边分别为a,b,c,若2bcsB=acsC+ccsA,b=2,则△ABC面积的最大值是( )
A.1B.3
C.2D.4
【答案】B
【解析】(1)∵2bcsB=acsC+ccsA,
∴可得:2sinBcsB=sinAcsC+sinCcsA=sinB,
∵sinB≠0,∴csB=12.B=60°
由余弦定理可得ac=a2+c2﹣4,
∴由基本不等式可得ac=a2+c2﹣4≥2ac﹣4,可得:ac≤4,当且仅当a=c时,“=”成立,
∴从而△ABC面积S=12acsinB=3,故△ABC面积的最大值为3.
故选:B.
11.已知双曲线x2a2﹣y2b2=1(a>0,b>0)的一条渐近线截椭圆x24+y2=1所得弦长为433,则此双曲线的离心率等于( )
A.2B.3
C.62D.6
【答案】B
【解析】双曲线x2a2﹣y2b2=1(a>0,b>0)的一条渐近线不妨为:bx﹣ay=0,则:&bx-ay=0&x24+y2=1,
消去y可得:x=±2aa2+4b2,y=±2ba2+4b2
一条渐近线截椭圆x24+y2=1所得弦长为433,
可得:4a2+4b2a2+4b2=43,可得2a2=b2=c2﹣a2,
解得e=ca=3.
故选:B.
12.设函数f'(x)是函数f(x)(x∈R)的导函数,已知f'(x)<f(x),且f'(x)=f'(4﹣x),f(4)=0,f(2)=1,则使得f(x)﹣2ex<0成立的x的取值范围是( )
A.(﹣2,+∞)B.(0,+∞)
C.(1,+∞)D.(4,+∞)
【答案】B
【解析】设F(x)=f(x)ex,则F'(x)=f'(x)-f(x)ex<0,
即函数F(x)在R 上单调递减,
因为f'(x)=f'(4﹣x),
即导函数y=f'(x)关于直线x=2对称,
所以函数y=f(x)是中心对称图形,且对称中心(2,1),
由于f(4)=0,即函数y=f(x)过点(4,0),
其关于点(2,1)的对称点(0,2)也在函数y=f(x)上,
所以有f(0)=2,
所以F(0)=f(0)e0=2,
而不等式f(x)﹣2ex<0即f(x)ex<2,
即F(x)<F(0),
所以x>0,
故使得不等式f(x)﹣2ex<0成立的x的取值范围是(0,+∞).
故选:B.
二、填空题(本题共4小题,每小题5分,共20分)
13.命题“∀x∈R,ex>0”的否定是 .
【答案】∃x∈R,ex≤0
【解析】(因为全称命题的否定是特称命题.所以,命题“∀x∈R,ex>0”的否定是:∃x∈R,ex≤0.
故答案为:∃x∈R,ex≤0.
14.已知函数 f(x)=2lnx 和直线 l:2x﹣y+6=0,若点 P 是函数 f(x)图象上的一点,则点 P到直线 l 的距离的最小值为 .
【答案】:855.
【解析】f′(x)=2x,
设与直线l平行且与函数f(x)的图象相切于点P(x0,y0)的直线方程为:2x﹣y+m=0,
则2x0=2,解得x0=1.∴P(1,0).
∴点 P到直线 l 的距离的最小值为切点P到直线l的距离d=|2-0+6|5=855.
故答案为:855.
15.A是半径为R的圆周上一个定点,在圆周上等可能地任取一点B,连接AB,则弦AB的长度小于3R的概率是
【答案】:23.
【解析】如图,
设圆O的半径为R,当∠AOB=120°时,AB=3R,
同理当∠AOC=120°时,AC=3R.
∴在圆周上等可能地任取一点与点A连接,则所得弦长小于3RR的概率为240°360°=23,
16.已知三棱锥P-ABC的四个顶点都在球O的球面上,PA=PB=PC,AB=2,BC=,AC=3,E,F分别为AC,PB的中点,EF=,则球O的体积为_______
【答案】
【解析】由已知可得,因,所以点在内的投影为的外心,所以平面,,所以,所以,又球心在上,设,则,所以,所以球体积,.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
已知函数f(x)=sin(2x+π6)+sin(2x-π6)+cs2x+a(a∈R,a为常数).
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调递减区间;
(Ⅲ)若x∈[0,π2]时,f(x)的最小值为﹣2,求a的值.
【解答】(I)f(x)=2sin2xcsπ6+cs2x+a=3sin2x+cs2x+a=2sin(2x+π6)+a
∴f(x)的最小正周期,T=2πω=2π2=π
(II)因为y=sinx的减区间为:2kπ+π2≤x≤2kπ+3π2,k∈Z
所以2kπ+π2≤2x+π6≤2kπ+3π2即kπ+π6≤x≤kπ+2π3(k∈Z)时,函数f(x)单调递减,
故所求区间为[kπ+π6,kπ+2π3](k∈Z)
(III)x∈[0,π2]时,2x+π6∈[π6,7π6]∴x=π2时
f(x)取得最小值∴2sin(2⋅π2+π6)+a=-2×12+a=-2∴a=-1.
18.(12分)
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥FAEC的体积.
证明 ∵△ABC为正三角形,E为BC中点,
∴AE⊥BC,
∴又B1B⊥平面ABC,AE⊂平面ABC,∴B1B⊥AE,
∴由B1B∩BC=B知,AE⊥平面B1BCC1,
又由AE⊂平面AEF,∴平面AEF⊥平面B1BCC1.
(2)解 设AB中点为M,连接CM,则CM⊥AB,
由平面A1ABB1⊥平面ABC,且平面A1ABB1∩平面ABC=AB知,CM⊥面A1ABB1,
∴∠CA1M即为直线A1C与平面A1ABB1所成的角,
∴∠CA1M=45°.
易知CM=eq \f(\r(3),2)×2=eq \r(3),在等腰Rt△CMA中,AM=CM=eq \r(3),
在Rt△A1AM中,A1A=eq \r(A1M2-AM2)=eq \r(2).
∴FC=eq \f(1,2)A1A=eq \f(\r(2),2),又S△AEC=eq \f(1,2)×eq \f(\r(3),4)×4=eq \f(\r(3),2),
∴V三棱锥FAEC=eq \f(1,3)×eq \f(\r(3),2)×eq \f(\r(2),2)=eq \f(\r(6),12).
19.(12分)
随着科技发展,手机成了人们日常生活中必不可少的通信工具,现在的中学生几乎都拥有了属于自己的手机了.为了调查某地区高中生一周使用手机的频率,某机构随机调查了该地区100名高中生某一周使用手机的时间(单位:小时),所取样本数据分组区间为[0,2)、[2,4)、[4,6)、[6,8)、[8,10)、[10,12)、[12,14],由此得到如图所示的频率分布直方图.
(1)求a的值并估计该地区高中生一周使用手机时间的平均值;
(2)从使用手机时间在[6,8)、[8,10)、[10,12)、[12,14]的四组学生中,用分层抽样方法抽取13人,则每层各应抽取多少人?
【解答】解:(1)由于小矩形的面积之和为1,则(a+0.075+4a+0.15+5a+0.05+0.025)×2=1,由此可得a=0.02.
该地区高中生一周使用手机时间的平均值为(1×0.02+3×0.075+5×0.08+7×0.15+9×0.1+11×0.05+13×0.025)×2=6.94.
(2)使用手机时间在[6,8)的学生有0.15×2×100=30人,使用手机时间在[8,10)的学生有0.02×5×2×100=20人,使用手机时间在[10,12)的学生有0.05×2×100=10人,使用手机时间在[12,14]的学生有0.025×2×100=5人,
故用分层抽样法从使用手机时间在[6,8),[8,10),[10,12),[12,14]的四组学生中抽样,抽取人数分别为13×3030+20+10+5=6,13×2030+20+10+5=4,13×1030+20+10+5=2,13×530+20+10+5=1.
20.(12分)
已知函数 .
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)讨论的单调性;
( = 3 \* ROMAN III)若存在最大值,且,求的取值范围.
【解答】 解:(Ⅰ)当时,.
.
所以.
又,
所以曲线在点处的切线方程是,
即.
(Ⅱ)函数的定义域为,
.
当时,由知恒成立,
此时在区间上单调递减.
当时,由知恒成立,
此时在区间上单调递增.
当时,由,得,由,得,
此时在区间内单调递增,在区间内单调递减.
( = 3 \* ROMAN III)由(Ⅱ)知函数的定义域为,
当或时,在区间上单调,此时函数无最大值.
当时,在区间内单调递增,在区间内单调递减,
所以当时函数有最大值.
最大值.
因为,所以有,解之得.
所以的取值范围是.
21.(12分)
已知椭圆的短轴长等于焦距,椭圆C上的点到右焦点的最短距离为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点且斜率为的直线与交于、两点,是点关于轴的对称点,证明:三点共线.
【解答】 ( = 1 \* ROMAN I)由题可知:
解得,
椭圆C的方程为
( = 2 \* ROMAN II)设直线:,,,,,
由得.
所以,.
而
,
∴三点共线
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4—4:坐标系与参数方程](10分)
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.已知圆C的极坐标方程为
ρ2﹣42ρcs(θ﹣π4)+6=0.
(1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(2)若点P(x,y)在圆C上,求x+y的最大值和最小值.
【解答】解:(1)由ρ2-42ρcs(θ-π4)+6=0,得
ρ2-42ρ(csθcsπ4+sinθsinπ4)+6=0,
即ρ2-42ρ(22csθ+22sinθ)+6=0,
ρ2﹣4ρcsθ﹣4ρsinθ+6=0,
即x2+y2﹣4x﹣4y+6=0为所求圆的普通方程,
整理为圆的标准方程(x﹣2)2+(y﹣2)2=2,
令x﹣2=2csα,y﹣2=2sinα.
得圆的参数方程为&x=2+2csα&y=2+2sinα (α为参数);
(2)由(1)得:
x+y=4+2(csα+sinα)=4+2sin(α+π4),
∴当sin(α+π4)=1时,x+y的最大值为6,
当sin(α+π4)=﹣1时,x+y的最小值为2.
故x+y的最大值和最小值分别是6和2.
23.[选修4—5:不等式选讲](10分)
已知不等式|x|+|x﹣3|<x+6的解集为(m,n).
(1)求m,n的值;
(2)若x>0,y>0,nx+y+m=0,求证:x+y≥16xy.
【解答】(1)解:不等式|x|+|x﹣3|<x+6,
当x≥3时,2x﹣3<x+6,即x<9,可得3≤x<9;
当0<x<3时,3<x+6,即x>﹣3,可得0<x<3;
当x≤0时,3﹣2x<x+6,即x>﹣1,可得﹣1<x≤0.
综上可得,原不等式的解集为(﹣1,9),
由不等式的解集为(m,n),
可得m=﹣1,n=9;
(2)证明:由(1)可得x>0,y>0,9x+y=1,
则1x+1y=(9x+y)(1x+1y)=9+1+yx+9xy≥10+2yx⋅9xy=16,
当且仅当y=3x=14时,取得等号,
则x+y≥16xy.
高中数学高考卷08--2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版): 这是一份高中数学高考卷08--2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版),共18页。试卷主要包含了测试范围等内容,欢迎下载使用。
高中数学高考卷06-2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版): 这是一份高中数学高考卷06-2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版),共14页。试卷主要包含了测试范围等内容,欢迎下载使用。
高中数学高考卷07-2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版): 这是一份高中数学高考卷07-2020年高考数学(文)名校地市好题必刷全真模拟卷(解析版),共16页。试卷主要包含了测试范围等内容,欢迎下载使用。












