第二章 进阶突破 试卷

第二章　进阶突破

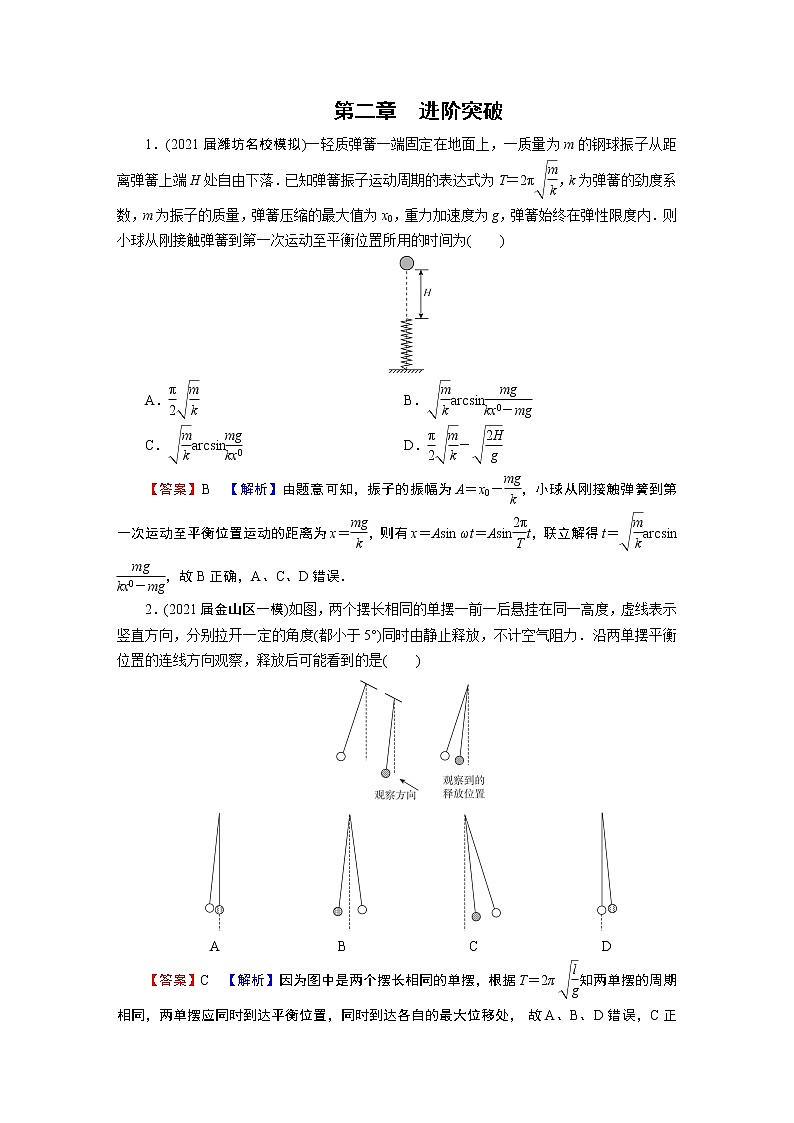
1．(2021届潍坊名校模拟)一轻质弹簧一端固定在地面上，一质量为m的钢球振子从距离弹簧上端H处自由下落．已知弹簧振子运动周期的表达式为T＝2π，k为弹簧的劲度系数，m为振子的质量，弹簧压缩的最大值为x0，重力加速度为g，弹簧始终在弹性限度内．则小球从刚接触弹簧到第一次运动至平衡位置所用的时间为(　　)

A．　　 B．arcsin

C．arcsin　　 D．－

【答案】B　【解析】由题意可知，振子的振幅为A＝x0－，小球从刚接触弹簧到第一次运动至平衡位置运动的距离为x＝，则有x＝Asin ωt＝Asint，联立解得t＝arcsin，故B正确，A、C、D错误．

2．(2021届金山区一模)如图，两个摆长相同的单摆一前一后悬挂在同一高度，虚线表示竖直方向，分别拉开一定的角度(都小于5°)同时由静止释放，不计空气阻力．沿两单摆平衡位置的连线方向观察，释放后可能看到的是(　　)

A B C D

【答案】C　【解析】因为图中是两个摆长相同的单摆，根据T＝2π知两单摆的周期相同，两单摆应同时到达平衡位置，同时到达各自的最大位移处，故A、B、D错误，C正确．

3．(2021届怀宁县第二中学月考)如图所示，一根不计质量的弹簧竖直悬吊质量为M的铁块，在其下方吸引了一质量为m的磁铁，已知弹簧的劲度系数为k，磁铁对铁块的最大吸引力等于3mg，不计磁铁对其他物体的作用并忽略阻力，为了使铁块和磁铁能够共同沿竖直方向作简谐运动，那么 (　　)

A．它处于平衡位置时弹簧的伸长量等于

B．振幅的最大值是

C．弹簧弹性势能最大时，弹力的大小等于2g

D．弹簧运动到最高点时，弹簧的弹力等于0

【答案】B　【解析】处于平衡位置时，合力为零，有(M＋m)g＝kx，所以伸长量为x＝，A错误；振幅最大的位置，弹性势能最大，形变量最大，设为Δx，由牛顿第二定律得kΔx－(M＋m)g＝(M＋m)a,3mg－mg＝ma，联立以上各式可得Δx＝，所以最大振幅为Δx－x＝，B正确；弹簧弹性势能最大时，弹力的大小为F弹＝kΔx＝3(M＋m)g，C错误；弹簧运动到最高点时，弹簧处于压缩状态，弹力不为零，D错误．

4．(2021届北京名校测试)如图所示，在电场强度为E的水平匀强电场中，有一足够大的绝缘光滑水平面，一根长为L的绝缘轻软细绳一端固定在平面上的O点，另一端系有一个质量为m、带电荷量为＋q的小球A(可看作质点)．当小球A在水平面上静止时，细绳被拉直且与OO′重合，OO′的方向与电场方向平行．在水平面内将小球由平衡位置拉开一小段距离，保持细绳拉直，直至细绳与OO′间有一个小角度θ后由静止释放，不计空气阻力，则下列说法中正确的是(　　)

A．小球A在运动过程中的加速度大小恒为a＝

B．细绳通过OO′后小球A速度为0时，细绳与OO′的夹角大于θ

C．细绳通过OO′时小球A的速度与其质量m无关

D．小球A释放后经历的时间，细绳会与OO′重合

【答案】D　【解析】在水平方向上，小球除了受电场力外，还受到绳子拉力作用，因此加速度不再是，A错误；由于运动的对称性，细绳通过OO′后小球A速度减小为0时，细绳与OO′的夹角仍为θ，B错误；根据动能定理Eql(1－cos  θ)＝mv2，小球A通过OO′时，质量越大， 速度越小，C错误；小球A的运动与单摆的运动类似，其等效重力加速度g′＝，代入单摆的振动周期公式，可得T＝2π，小球A经 细绳恰好与OO′重合，D正确．

5．(2021届德州市名校期末)如图所示，一轻质弹簧下端系一质量为m的书写式激光笔，组成一弹簧振子，并将其悬挂于教室内一体机白板的前方．使弹簧振子沿竖直方向上下自由振动，白板以速率v水平向左匀速运动，激光笔在白板上留下如图所示的书写印迹，图中相邻竖直虚线的间隔均为x0(未标出)，印迹上P、Q两点的纵坐标分别为y0和－y0．忽略空气阻力，重力加速度为g，则(　　)

A．该弹簧振子的振幅为2y0

B．该弹簧振子的振动周期为

C．激光笔在留下P、Q两点时加速度相同

D．激光笔在留下PQ段印迹的过程中，弹簧弹力对激光笔做功为－2mgy0

【答案】D　【解析】记录纸匀速运动，振子振动的周期等于记录纸运动位移2x0所用的时间，则周期T＝，振幅为A＝y0，A、B错误；加速度是矢量，激光笔在留下P、Q两点时加速度大小相等，方向相反，C错误；在激光笔留下PQ段印迹的过程中，根据动能定理可知，合外力做功为零，但重力做正功为2mgy0，故弹力对激光笔做负功为－2mgy0，D正确．

6．(多选)(2020年赣州名校期中)甲、乙两弹簧振子水平放置时的振动图像如图所示，则可知(　　)

A．两弹簧振子完全相同

B．振子甲速度为零时，振子乙速度最大

C．两弹簧振子所受回复力最大值之比F甲∶F乙＝2∶1

D．振子乙速度为最大时，振子甲速度不一定为零

【答案】BD　【解析】两弹簧振子不一定完全相同，A错误；分析振动图像可知，振子甲速度为零时，振子乙处于平衡位置，速度最大，B正确； 弹簧振子的回复力F＝－kx，本题中k可能不同，则无法判断两振子的回复力最大值的关系，C错误；分析振动图像可知，振子乙速度最大时，振子甲可能处于最大位移处，也可能处于平衡位置，故振子甲速度不一定为零，D正确．

7．(多选)(2021届祁县名校月考)如图所示，虚线和实线分别为甲、乙两个弹簧振子做简谐运动的图像．已知甲、乙两个振子质量相等，则(　　)

A．甲、乙两振子的振幅分别为2 cm、1 cm

B．甲、乙两个振子的相位差总为π

C．前2秒内甲、乙两振子的加速度均为正值

D．第2秒末甲的速度最大，乙的加速度最大

【答案】AD　【解析】根据振动图像，甲振子的振幅为2 cm、乙振子的振幅为1 cm，A正确；由于两个振子的周期和频率不同，其相位差也会变化，B错误；前2秒内，甲在平衡位置的上方，加速度指向平衡位置，方向向下，为负；而乙在平衡位置的下方，加速度指向平衡位置，方向向上，为正，C错误；第2秒末甲处于平衡位置，速度最大加速度最小，乙处于波谷，速度最小加速度最大，D正确．

8．(多选)(2021届河南校级模拟)某弹簧振子做简谐运动，其位移—时间关系式为x＝10cos(4πt)cm.下列说法中正确的是(　　)

A．弹簧振子的振幅为10 cm

B．弹簧振子的频率是2 Hz

C．在t＝0.125 s时，弹簧振子的速度最大

D．在t＝0.25 s时，弹簧振子的回复力最大

【答案】BCD　【解析】据题质点做简谐运动的位移表达式为x＝10cos(4πt) cm，则知振幅为A＝10 cm，A错误；根据4π＝2πf，可得频率为f＝2 Hz，B正确；在t＝0.125 s时，x＝10cos(4πt)＝0，可知该时刻质点的位移为零，则速度最大，C正确；在t＝0.25 s时，x＝10cos(4πt)＝－10 cm，位移最大，回复力最大，D正确．

9．(2020年成都校级模拟)用单摆测定重力加速度的实验中：

(1)实验时用20分度的游标卡尺测量摆球直径，示数如图甲所示，该摆球的直径d＝________mm.

(2)悬点到小球底部的长度l0，示数如图乙所示，l0＝________cm.

(3)实验时用拉力传感器测得摆线的拉力大小F随时间t变化的图像如图丙所示，然后使单摆保持静止，得到如图丁所示的F－t图像．那么：

①重力加速度的表达式g＝____________(用题目中的物理量d、l0、t0表示)．

②设摆球在最低点时Ep＝0，已测得当地重力加速度为g，单摆的周期用T表示，那么测得此单摆摆动时的机械能E的表达式是________．

A．　　　 B．

C．　　　 D．

(4)在实验中测得的g值偏小，可能原因是___________．

A．测摆线时摆线拉得过紧

B．摆线上端未牢固地系于悬点，振动中出现了松动，使摆线长度增加了

C．开始计时时，停表过迟按下

D．实验中误将n 次计为n－1次

E．以摆球直径和摆线长之和作为摆长来计算

【答案】(1)11.65　(2)100.30(100.20～100.30均可)

(3)①　②B　(4) BD

【解析】(1)游标卡尺的精度为＝0.05 mm，读数为11 mm＋13×0.05  mm＝11.65 mm.

(2)刻度尺的精度为＝0.1 cm，读数为100.30 cm.

(3)①在单摆摆动的过程中，每个周期中有两次拉力最大值，由图丙知单摆的周期T＝4t0，根据单摆的周期公式T＝2π可知g＝＝；

②单摆经过最低点时，根据丙图可知F1－mg＝，根据丁图可知F3＝mg，小球的摆长为l＝，则小球在最低点的动能为Ek＝mv2＝，小球摆动过程机械能守恒，则E＝Ek＋Ep＝，故B正确．

(4)测摆线时摆线拉得过紧，则摆长的测量值偏大，根据g＝可知重力加速测量值偏大，A错误；摆线长度增加，则摆长的测量值偏小，所以重力加速度测量值偏小，B正确；开始计时时，停表过迟按下，则测量周期偏小，重力加速度测量值偏大，C错误；实验中误将n 次计为n－1次，根据T＝可知周期测量值偏大，所以重力加速度测量值偏小，D正确；以摆球直径和摆线长之和作为摆长来计算，重力加速度测量值偏大，E错误．

10．(2021届北京模拟)万有引力和库仑力有类似的规律，有很多可以类比的地方．已知引力常量为G，静电力常量为k.

(1)用定义静电场强度的方法来定义与质量为M的质点相距r处的引力场强度EG的表达式；

(2)质量为m、电荷量为e的电子在库仑力的作用下以速度v绕原子核做匀速圆周运动，该模型与太阳系内行星绕太阳运转相似，被称为“行星模型”，如图甲．已知在一段时间内，电子走过的弧长为s，其速度方向改变的角度为θ(弧度)．不考虑电子之间的相互作用，求出原子核的电荷量Q；

(3)如图乙，用一根长为L的绝缘细线悬挂一个可看成质点的金属小球，质量为m，电荷量为－q.悬点下方固定一个足够大的水平放置的均匀带正电的介质平板．小球在竖直平面内做小角度振动．已知重力加速度为g，不计空气阻力．

①已知忽略边缘效应的情况下，带电平板所产生的静电场的电场线都垂直于平板，静电场的电场力做功与路径无关．请证明：带电平板所产生的静电场是匀强电场；

②在上述带电平板附近所产生的静电场场强大小为E，求：金属小球的振动周期．

【答案】(1)EG＝G　(2)Q＝

(3)①见解析　②T＝2π

【解析】(1)EG的表达式为EG＝G.

(2)根据k＝m，R＝，

联立得Q＝.

(3)①反证法．

方法1：如图，

若存在电场线平行但不等间距的静电场，则可以引入试探电荷＋q，让＋q从a点沿矩形路线abcda(ab与电场线平行，bc边与电场线垂直)运动一周回到a点．设ab处的场强大小为E1，cd处的场强大小为E2，根据功的定义，电场力做的总功Waa＝Wab＋Wbc＋Wcd＋Wda.

其中Wab＝qE1xab，

Wcd＝－qE2xab，

bc段和da段电场力始终与运动方向垂直

故Wbc＝Wda＝0，

得Waa＝Wab＋Wbc＋Wcd＋Wda＝qE1xab＋0＋0－qE2xab＝q(E1－E2)xab>0．

但根据电场力做功的特点，做功与路径无关，故Waa＝0．

上述假设矛盾，故不存在电场线平行但不等间距的静电场．

方法2：如图，若存在电场线平行但不等间距的静电场，则可以引入试探电荷＋q，让＋q从a点分别沿矩形abcd(ab与电场线平行，bc边与电场线垂直)的abc和adc运动到c点．设ab处的场强大小为E1，cd处的场强大小为E2，根据功的定义，路径ac和adc电场力做的功分别为

Wabc＝Wab＋Wbc，

Wadc＝Wcd＋Wda.

其中Wab＝qE1xab，

Wcd＝－qE2xdc＝－qE2xab.

bc段和da段电场力始终与运动方向垂直

故Wbc＝Wda＝0，

得Wabc＝Wab＋Wbc＝qE1xab＋0，

Wadc＝Wcd＋Wda＝0－qE2xab，

故Wabc≠Wadc

但根据电场力做功的特点，做功与路径无关，故Wabc＝Wadc.

上述假设矛盾，故不存在电场线平行但不等间距的静电场．

②电场力F电＝qE，

等效重力加速度g′＝＝，

小球在库仑力作用下的振动周期

T＝2π＝2π.