高中数学高考2022届高考数学一轮复习(新高考版) 第5章 强化训练5　平面向量中的综合问题课件PPT

这是一份高中数学高考2022届高考数学一轮复习(新高考版) 第5章 强化训练5　平面向量中的综合问题课件PPT，共33页。PPT课件主要包含了1求实数λ的值等内容，欢迎下载使用。

1.(2021·甘肃诊断)已知平面向量a，b满足a＝(1，－2)，b＝(－3，t)，且a⊥(a＋b)，则|b|等于
解析　a＋b＝(1，－2)＋(－3，t)＝(－2，t－2)，由于a⊥(a＋b)，所以a·(a＋b)＝0，即1×(－2)＋(－2)×(t－2)＝0，解得t＝1，
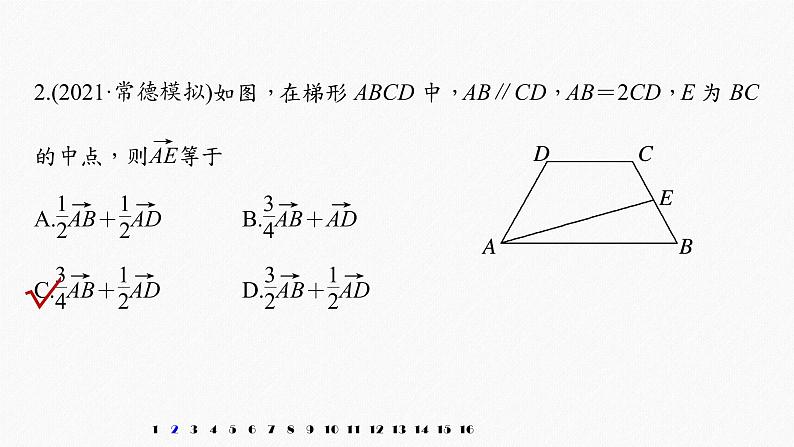
解析　设F为AB的中点，连接DF，如图，∵AB∥CD，AB＝2CD，∴BF∥CD，且BF＝CD，∴四边形BFDC为平行四边形，
解析　因为a⊥(a＋2b)，所以a·(a＋2b)＝a2＋2a·b＝4＋2a·b＝0，a·b＝－2，
4.(2020·河北“五个一”名校联考)若两个非零向量a，b满足|a＋b|＝|a－b|＝2|a|，则向量a＋b与a－b的夹角是
解析　将|a＋b|＝|a－b|＝2|a|平方得a2＋2a·b＋b2＝a2－2a·b＋b2＝4a2，
a·(a＋b)＝|a|2＋a·b＝－2，则a·b＝－6，D正确；
6.(多选)若a，b，c均为单位向量，且a·b＝0，(a－c)·(b－c)≤0，则|a＋b－c|的值可能为
解析　因为a，b，c均为单位向量，且a·b＝0，(a－c)·(b－c)≤0，所以a·b－c·(a＋b)＋c2≤0，所以c·(a＋b)≥1，
所以选项C，D不正确，故选AB.
所以3×(m＋1)＝2m，所以m＝－3.
8.已知a＝(2＋λ，1)，b＝(3，λ)，若a与b的夹角为钝角，则实数λ的取值范围是________________.
解析　由题意得，a·b<0且a与b不共线，即3(2＋λ)＋λ<0且(2＋λ)λ≠3，
解析　如图所示，建立直角坐标系.
解析　∵△ABC的重心为G，
11.已知向量a，b的夹角为60°，且a＝(1,0).(1)若|b|＝2，求b的坐标；
解　设b＝(x，y)，因为向量a，b的夹角为60°，且a＝(1,0)，|b|＝2.
(2)若(a＋b)⊥(a－b)，求|a－2b|的值.
解　因为(a＋b)⊥(a－b)，所以(a＋b)·(a－b)＝a2－b2＝|a|2－|b|2＝0，由于a＝(1,0)，所以|a|＝|b|＝1，
∵∠B＝60°，∴∠DAB＝120°，
解　如图，过点A作AO⊥BC，垂足为O，
以O为原点，以BC，OA所在直线为坐标轴建立平面直角坐标系，
A.等边三角形 B.三边均不相等的三角形C.等腰非等边三角形 D.直角三角形
所以△ABC为等腰非等边三角形.
解析　如图所示，D，E分别是BC，AC的中点，
15.已知三个向量a，b，c共面，且均为单位向量，a·b＝0，则|a＋b－c|的取值范围是
解析　因为a·b＝0，所以|a＋b|2＝a2＋2a·b＋b2＝2，
所以|a＋b－c|2＝a2＋b2＋c2＋2a·b－2(a＋b)·c＝3－2(a＋b)·c，则当c与(a＋b)同向时，(a＋b)·c最大，
当c与(a＋b)反向时，(a＋b)·c最小，|a＋b－c|2最大，
(1)求证：△ABC为等腰三角形；
故△ABC为等腰三角形.