河北省保定市安新县2022-2023学年九年级上学期期末考试数学试题

2022—2023学年度第一学期期末调研考试

九年级数学试题

注意：本份试卷共8页，三道大题，26个小题；满分120分，时间120分钟。

一、选择题（本大题共16个小题，共42分.1~10小题各3分，11~16小题各2分.在每小题给出的四个选项中，只有一项是符合题目要求的.请将正确的选项填在下表中）

1.下面的图形中，既是轴对称图形又是中心对称图形的是（    ）

A. B. C. D.

2.下列事件中，是必然事件的是（    ）

A.任意买一张电影票，座位号是2的倍数 B.明天一定会下雨

C.车辆随机到达一个路口，遇到红灯 D.13个人中至少有两个人生肖相同

3.在中，，，，以为圆心，为半径作，则点与的位置关系是（    ）

A.点在内 B.点在上 C.点在外 D.无法确定

4.若点，，都在反比例函数的图象上，则，，的大小关系是（    ）

A. B. C. D.

5.如图，是正五边形的外接圆，点是的一点，则的度数是（    ）

A.30° B.36° C.45° D.72°

6.关于抛物线，下列说法错误的是（    ）

A.开口向下  B.顶点坐标是

C.当时，随的增大而增大 D.对称轴直线

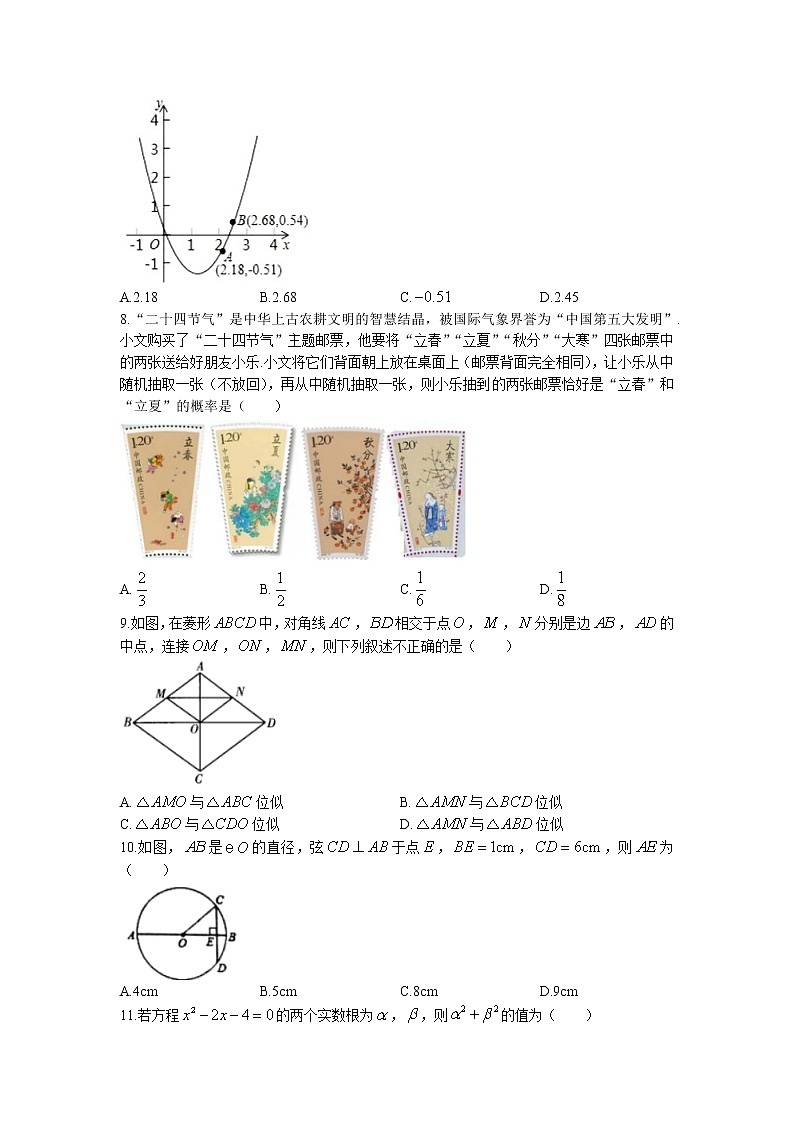
7.如图，点，在二次函数的图象上，则方程的一个近似解可能是（    ）

A.2.18 B.2.68 C. D.2.45

8.“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（    ）

A. B. C. D.

9.如图，在菱形中，对角线，相交于点，，分别是边，的中点，连接，，，则下列叙述不正确的是（    ）

A.与位似 B.与位似

C.与位似 D.与位似

10.如图，是的直径，弦于点，，，则为（    ）

A.4cm B.5cm C.8cm D.9cm

11.若方程的两个实数根为，，则的值为（    ）

A.12 B.10 C.4 D.

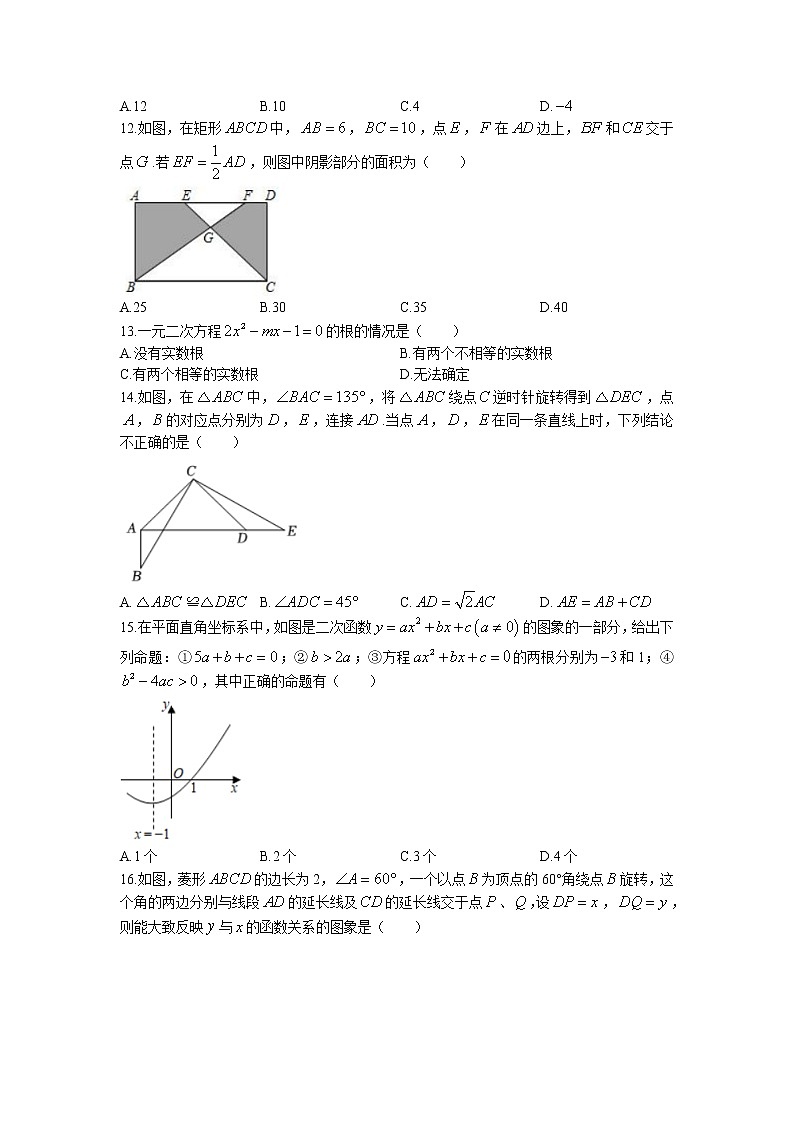
12.如图，在矩形中，，，点，在边上，和交于点.若，则图中阴影部分的面积为（    ）

A.25 B.30 C.35 D.40

13.一元二次方程的根的情况是（    ）

A.没有实数根  B.有两个不相等的实数根

C.有两个相等的实数根  D.无法确定

14.如图，在中，，将绕点逆时针旋转得到，点，的对应点分别为，，连接.当点，，在同一条直线上时，下列结论不正确的是（    ）

A. B. C. D.

15.在平面直角坐标系中，如图是二次函数的图象的一部分，给出下列命题：①；②；③方程的两根分别为和1；④，其中正确的命题有（    ）

A.1个 B.2个 C.3个 D.4个

16.如图，菱形的边长为2，，一个以点为顶点的60°角绕点旋转，这个角的两边分别与线段的延长线及的延长线交于点、，设，，则能大致反映与的函数关系的图象是（    ）

A. B. C. D.

二、填空题（本大题共3个小题，每小题3分，共9分.其中18小题第一空2分，第二空1分，19小题每空1分.把答案写在题中横线上）

17.中，点、分别是、的中点，若，则______.

18.如图，小明用半径为20，圆心角为的扇形，围成了一个底面半径为5的圆锥.

（1）扇形的圆心角为______；

（2）一只蜘蛛从圆锥底面圆周上一点出发，沿圆锥的侧面爬行一周后回到点的最短路程是______.

19.如图，在平面直角坐标系中，为原点，每个小方格的边长为1个单位长度.正方形顶点都在格点上，其中点的坐标为.

（1）若将正方形绕点顺时针方向旋转90°，点到达点，点到达点，点到达点，此时的坐标是______；

（2）若线段的长度与点的横坐标的差恰好是一元二次方程的一个根，线段______，的值为______.

三、解答题（本大题共7小题，共69分.解答应写出文字说明、证明过程或演算步骤）

20.（本题满分9分）用适当的方法解下列一元二次方程：

（1）； （2）.

21.（本题满分9分）

“石头、剪子、布”是一个广为流传的游戏，规则是：甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种，其中“石头”赢“剪子”，“剪子”赢“布”，“布”赢“石头”，手势相同不分输赢.假设甲、乙两人每次都随意并且同时做出3种手势中的1种.

（1）甲每次做出“石头”手势的概率为______；

（2）用画树状图或列表的方法，求乙不输的概率.

22.（本题满分9分）

心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化.开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散.经过实验分析可知，学生的注意力指标数随时间（分钟）的变化规律如图所示（其中、分别为线段，为双曲线的一部分）：

（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？

（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？请说明理由.

23.（本题满分10分）

如图，在中，，为边上的中线，于点.

（1）求证：；

（2）若，，求线段的长.

24.（本题满分10分）

如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度为10米），围成中间隔有一道篱笆的长方形花圃.设花圃的宽为米，面积为米.

（1）求与的函数关系式，并求出自变量的取值范围；

（2）如果要围成面积为45米的花圃，的长是多少米？

（3）能围成面积比45米更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由.

25.（本题满分10分）

筒车是我国古代利用水力驱动的灌溉工具，车轮缚以竹筒，旋转时低则舀水，高则泻水.如图，水力驱动筒车按逆时针方向转动，竹筒把水引至处，水沿射线方向泻至水渠，水渠所在直线与水面平行.设筒车为，与直线交于，两点，与直线交于，两点，恰有，连接，.

（1）求证：为的切线；

（2）筒车的半径为3m，，.当水面上升，，，三点恰好共线时，如图，则______°，______°；

（3）在（2）的条件下，直接写出筒车在水面下的最大深度（精确到0.1m，参考值：，）.

26.（本题满分12分）

如图，抛物线过点、两点，点、关于抛物线的对称轴对称，过点作直线轴，交轴于点.

（1）求抛物线的表达式；

（2）直接写出点的坐标，并求出的面积；

（3）点是抛物线上一动点，且位于第四象限，当的面积为6时，求出点的坐标；

（4）已知点在直线上运动，点在轴上运动，若是以点为直角顶点的等腰直角三角形，请直接写出此时的面积.

2022—2023（1）九年级数学参考答案及评分标准

说明：

1.在阅卷过程中，如果考生还有其它正确解法，可参照评分参考酌情给分；

2.填空题缺少必有的单位或答案不完整不得分；

3.坚持每题评阅到底的原则，当考生的解答在某一步出现错误，影响了后继部分时，如果该步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严置的错误，就不给分；

4.解答右端所注分数，一般表示正确做到这一步应得的累积分数.

一、选择题（本大题有16小题，共42分.1~10小题各3分，11~16小题各2分）

二、填空题（本大题共3个小题，每小题3分，共9分.其中18小题第一空2分，第二空1分，19小题每空1分）

17.8； 18.（1）90°；（2）； 19.（1）；（2），.

三、解答题（本大题有7小题，共69分）

20.解：（1），……1分，……2分

，……3分，……4分，；……5分

（2），……1分，……2分

则或，……3分，. ……4分

21.（1）……3分

（2）树状图如图所示：

……6分

甲、乙两人同时做出手势共有9种等可能结果，其中乙不输的共有6种，∴……8分

所以乙不输的概率是. ……9分

22.解：（1）设线段所在直线的解析式为，

把代入得，∴. ……1分

设，所在双曲线的解析式为，把代入得，∴. ……3分

当时，；当时，.

∴.∴第30分钟学生的注意力更集中. ……5分

（2）能……6分

令，则，∴. ……7分

令，则，∴. ……8分

∵，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目. ……9分

23.（1）证明：∵，为边上的中线，∴，，∴.

∵，∴，∴.∴. ……5分

（2）解：由（1）知，在中，.

∵，∴，即. ……10分

24.解：（1）由题可知，花圃的宽为米，则为米，面积，……3分

由，得. ……4分

（2）令，则，即，解得，.

∵，∴不合题意，舍去，

答：花圃的宽为5米。……6分

（3）能围成. ……7分

∵，对称轴为，∴在对称轴右侧，随的增大而减小，∴当时，有最大值，

此时，故能围成面积比45平方米更大的花圃

围法：（米），即花圃的长为10米，宽为米，这时有最大面积平方米。……10分

25.（1）证明：连接并延长交于，连接，∴为的直径，

∴，∴，∵，∴，

又∵，∴，∴，

又∵，∴，∴，∴为的切线；……4分

（2）60；45；……8分（每空2分）

（3）0.9. ……10分

26.解：（1）把点，代入抛物线中，

得，解得：，∴抛物线的表达式为：；……3分

（2）点的坐标为，……4分

又∵点的坐标为，∴，∴；……5分

（3）如图，

过点作交于点，

设点，根据题意，得：，，，

∴，

，∴，

解得：（舍去），，∴点坐标为. ……9分

（4）或.……12分

（写对1个给1分，写对2个给3分）