高中数学高考32第一部分 板块三 第6讲　数学文化

这是一份高中数学高考32第一部分 板块三 第6讲　数学文化，共6页。
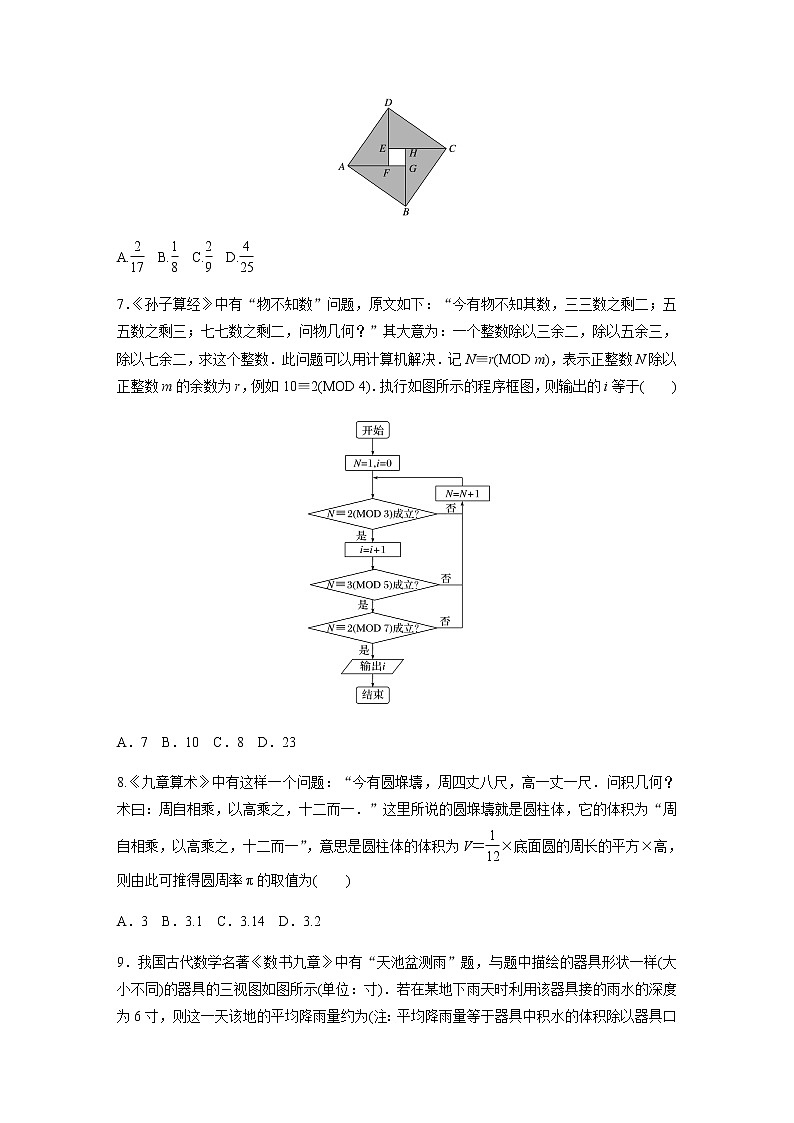
第6讲　数学文化1．(2019·东北三省四市教研联合体模拟)中国有个名句“运筹帷幄之中，决胜千里之外．”其中的“筹”取意是指《孙子算经》中记载的算筹．古代是用算筹来进行计算的．算筹是将几寸长的小竹棍摆在地面上进行运算．算筹的摆放形式有纵横两种(如图所示)．表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列．但各位数码的筹式要纵横相间，个位、百位、万位数用纵式表示，十位、千位、十万位数用横式表示．以此类推．例如3 266用算筹表示就是，则8 771用算筹可表示为(　　)2．(2018·晋中榆社中学模拟)大衍数列，来源于《乾坤谱》中对《易传》“大衍之数五十”的推论．主要用于解释中国传统文化中的太极衍生原理．数列中的每一项，都代表太极衍生过程中曾经经历过的两仪数量总和，是中华传统文化中隐藏着的世界数学史上第一道数列题．其规律是：偶数项是序号平方再除以2，奇数项是序号平方减1再除以2，其前10项依次是0,2,4,8,12,18,24,32,40,50，…，如图所示的程序框图是为了得到大衍数列的前100项而设计的，那么在两个“”中，可以先后填入(　　)A．n是偶数？n≥100?   B．n是奇数？n≥100?C．n是偶数？n>100?   D．n是奇数？n>100?3．“干支纪年法”是中国历法上自古以来就一直使用的纪年方法．干支是天干和地支的总称．天干、地支互相配合，配成六十组为一周，周而复始，依次循环．甲、乙、丙、丁、戊、己、庚、辛、壬、癸为天干；子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥为地支．如：公元1984年为农历甲子年、公元1985年为农历乙丑年，公元1986年为农历丙寅年．则2049年为农历(　　)A．己亥年  B．己巳年  C．己卯年  D．戊辰年方法二　易知(年份－3)除以10所得的余数对应天干，则2 049－3＝2 046,2 046除以10所得的余数是6，即对应的天干为“己”．(年份－3)除以12所得的余数对应地支，则2 049－3＝2 046，2 046除以12所得的余数是6，即对应的地支为“巳”，所以2049年为农历己巳年．4．(2018·北京)“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f，则第八个单音的频率为(　　)A.f  B.f  C.f  D.f5．(2019·湖南长沙雅礼中学模拟)我国古代数学著作《九章算术》有如下问题：“今有金箠，长5尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何？”，意思是“现有一根金箠，长5尺，一头粗，一头细，在粗的一端截下1尺，重4斤，在细的一端截下1尺，重2斤，问依次每一尺各重多少斤？”设该金箠由粗到细是均匀变化的，其重量为M，现将该金箠截成长度相等的10段，记第i段的重量为ai(i＝1,2，…，10)，且a1<a2…<a10，若48ai＝5M，则i等于(　　)A．4  B．5  C．6  D．76．(2019·长沙模拟)如图所示是2002年8月在北京召开的国际数学家大会会标图案，该图案的设计基础是赵爽弦图，以纪念我国古代数学家赵爽用此图证明了勾股定理．如图是用4个全等的直角三角形以斜边为边长拼成的一个正方形．假设直角三角形的直角边长分别为3,5，在正方形ABCD中随机取一点，则此点取自四边形EFGH内的概率是(　　)A.  B.  C.  D.7．《孙子算经》中有“物不知数”问题，原文如下：“今有物不知其数，三三数之剩二；五五数之剩三；七七数之剩二，问物几何？”其大意为：一个整数除以三余二，除以五余三，除以七余二，求这个整数．此问题可以用计算机解决．记N≡r(MOD m)，表示正整数N除以正整数m的余数为r，例如10≡2(MOD 4)．执行如图所示的程序框图，则输出的i等于(　　)A．7  B．10  C．8  D．238.《九章算术》中有这样一个问题：“今有圆堢壔，周四丈八尺，高一丈一尺．问积几何？术曰：周自相乘，以高乘之，十二而一．”这里所说的圆堢壔就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”，意思是圆柱体的体积为V＝×底面圆的周长的平方×高，则由此可推得圆周率π的取值为(　　)A．3  B．3.1  C．3.14  D．3.29．我国古代数学名著《数书九章》中有“天池盆测雨”题，与题中描绘的器具形状一样(大小不同)的器具的三视图如图所示(单位：寸)．若在某地下雨天时利用该器具接的雨水的深度为6寸，则这一天该地的平均降雨量约为(注：平均降雨量等于器具中积水的体积除以器具口的面积．参考公式：圆台的体积V＝πh(R2＋r2＋R·r)，其中R，r分别表示上、下底面的半径，h为高)(　　)A．2寸  B．3寸  C．4寸  D．5寸10．(2018·河北省衡水金卷模拟)我国古代《九章算术》里，记载了一个“商功”的例子：今有刍童，上广二丈，袤三丈，下广三丈，袤四丈，高三丈．问积几何？其意思是：今有上下底面皆为长方形的草垛(如图所示)，上底宽2丈，长3丈；下底宽3丈，长4丈，高3丈．问它的体积是多少？该书提供的算法是：上底长的2倍与下底长的和与上底宽相乘，同样下底长的2倍与上底长的和与下底宽相乘，再次相加，再乘以高，最后除以6.则这个问题中的刍童的体积为(　　)A．13.25立方丈   B．26.5立方丈C．53立方丈   D．106立方丈11．(2019·达州模拟)里氏震级是由古登堡和里克特制定的一种表明地震能量大小的标度，用来表示测震仪衡量地震能量的等级，地震能量越大，地震仪记录的震波的振幅就越大，其计算公式为M＝lg A－lg A0，其中A，A0分别是距震中100公里处接收到的所关注的这个地震和0级地震的震波的最大振幅，则7级地震震波的最大振幅是5级地震震波的最大振幅的(　　)A．10倍  B．20倍  C．50倍  D．100倍12．(2019·晋中调研)艾萨克·牛顿(1643年1月4日—1727年3月31日)，英国皇家学会会长，英国著名物理学家，同时在数学上也有许多杰出贡献，牛顿用“作切线”的方法求函数f(x)零点时给出一个数列{xn}：满足xn＋1＝xn－，我们把该数列称为牛顿数列．如果函数f(x)＝ax2＋bx＋c(a>0)有两个零点1,2，数列{xn}为牛顿数列，设an＝ln ，已知a1＝1，xn>2，{an}的前n项和为Sn，则S2 018＋1等于(　　)A．2 018  B．2 019  C．22 018  D．22 01913．(2019·合肥模拟)部分与整体以某种相似的方式呈现称为分形．谢尔宾斯基三角形是一种分形，由波兰数学家谢尔宾斯基1915年提出．具体操作是取一个实心正三角形，沿三角形的三边中点连线，将它分成4个小三角形，去掉中间的那一个小三角形后，对其余3个小三角形重复上述过程逐次得到各个图形，如图．若在上述图(3)中随机选取一个点，则此点取自阴影部分的概率为________．14．(2019·西安期中)古希腊毕达哥拉斯学派的数学家研究过各种多边形数．如三角形数1,3,6,10，…，第n个三角形数为＝n2＋n.记第n个k边形数为N(n，k)(k≥3)，以下列出了部分k边形数中第n个数的表达式：三角形数N(n,3)＝n2＋n；正方形数N(n,4)＝n2；五边形数N(n,5)＝n2－n；六边形数N(n,6)＝2n2－n；…，可以推测N(n，k)的表达式，由此计算N(10,24)＝________.15．《数书九章》三斜求积术：“以小斜幂，并大斜幂，减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂，减上，余四约一，为实，一为从隅，开平方得积”．秦九韶把三角形的三条边分别称为小斜、中斜和大斜，“术”即方法．以S，a，b，c分别表示三角形的面积、大斜、中斜、小斜；ha，hb，hc分别为对应的大斜、中斜、小斜上的高；则S＝ ＝aha＝bhb＝chc.若在△ABC中，ha＝，hb＝2，hc＝3，根据上述公式，可以推出该三角形外接圆的半径为________．16.(2019·湖北八校联考)祖暅是我国南北朝时期杰出的数学家和天文学家，是祖冲之的儿子．他提出了一条原理：“幂势既同，则积不容异．”这里的“幂”指面积，“势”指高．这句话的意思是：如果两个等高的几何体在同高处截得两几何体的截面积恒等，那么这两个几何体的体积相等．设由椭圆＋＝1(a>b>0)所围成的平面图形绕y轴旋转一周后，得一橄榄球状的几何体(称为椭球体)，如图，请类比此法，求出椭球体体积，其体积等于________．