八年级下册2.5.1矩形的性质说课课件ppt

这是一份八年级下册2.5.1矩形的性质说课课件ppt，共17页。PPT课件主要包含了对边平行且相等，对角相等邻角互补，对角线互相平分，中心对称图形，四边形具有不稳定性，知识回顾，新知探究，平行四边形，四边形，它还有特殊性质等内容，欢迎下载使用。

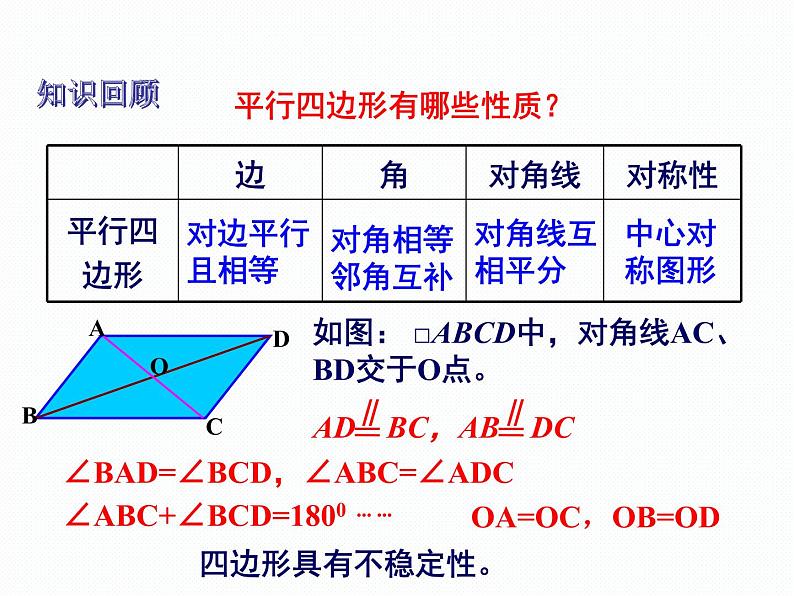
平行四边形有哪些性质？
如图： □ABCD中，对角线AC、BD交于O点。
∠BAD=∠BCD，∠ABC=∠ADC∠ABC+∠BCD=1800 ... ...
OA=OC，OB=OD
在小学，我们初步认识了长方形，观察图中的长方形，它是什么平行四边形吗？它有什么特点呢？
细心观察平行四边形内角的变化
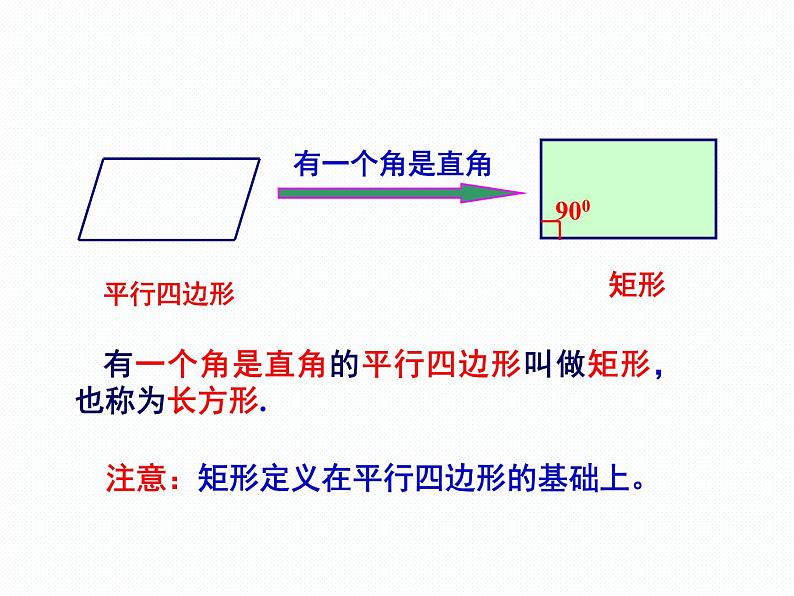
把平行四边形的角变成直角。
有一个角是直角的平行四边形叫做矩形，也称为长方形.
注意：矩形定义在平行四边形的基础上。
由矩形定义讨论：矩形是平行四边形吗？它具有平行四边形的性质吗？
四边形、平行四边形、矩形的关系如图：
有一个角是直角的平行四边形叫矩形
矩形是特殊的平行四边形
对边平行且相等；对角相等；对角线互相平分；是中心对称图形。
我们发现矩形对边平行且相等，因此，它是平行四边形.具有平行四边形的性质：
平行四边形变成矩形时，图形的内角有何特征？
矩形的四个角都是直角.
综合起来：由于矩形是平行四边形，因此，可得矩形的边、角性质：
矩形的四个角都是直角，对边相等，对角线互相平分；矩形是中心对称图形，对角线的交点是它的对称中心.
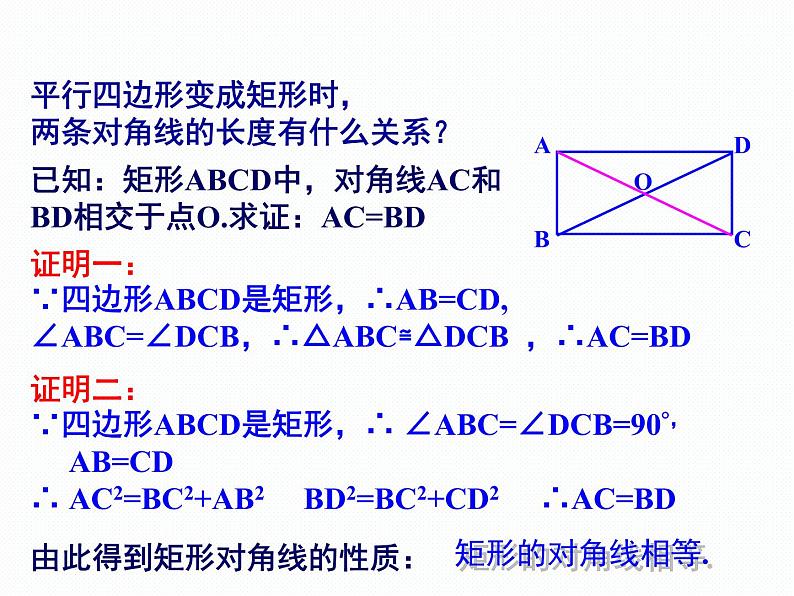
平行四边形变成矩形时，两条对角线的长度有什么关系？
已知：矩形ABCD中，对角线AC和BD相交于点O.求证：AC=BD
证明一：∵四边形ABCD是矩形，∴AB=CD,∠ABC=∠DCB，∴△ABC≌△DCB ，∴AC=BD
证明二：∵四边形ABCD是矩形，∴ ∠ABC=∠DCB=90°， AB=CD∴ AC2=BC2+AB2 BD2=BC2+CD2 ∴AC=BD
由此得到矩形对角线的性质：
例1.如图，矩形ABCD的两条对角线AC ，BD相交于点O，AC = 4 cm， ∠AOB = 60°. 求BC的长.
∴ △AOB是等边三角形.
∴ AB=OA=2cm.
又∠AOB = 60°，
∵ ∠ABC = 90°，
∴ 在Rt△ABC中，
解：∵ □ABCD是矩形，
在纸上画一个矩形ABCD(如图)，把它剪下来，怎样折叠能使矩形在折痕两旁的部分互相重合？满足这个要求的折叠方法有几种？
由此猜测：矩形是轴对称图形吗？如果是，它有几条对称轴？你的猜测正确吗？
过点O作直线EF⊥BC，且分别与边BC ，AD相交于点E，F.
由于AD∥BC，因此EF⊥AD. 同理，直线EF是线段AD的垂直平分线.
因此△OBC是等腰三角形，从而直线EF是线段BC的垂直平分线.
因此点B和点C关于直线EF对称，点A和点D关于直线EF对称，从而在关于直线EF的轴反射下，矩形ABCD的像与它自身重合，因此矩形ABCD是轴对称图形，点E、F分别是AD、BC的中点，直线EF是矩形ABCD的一条对称轴.
类似地，过点O作直线MN⊥AB，且分别与边AB，DC相交于点M，N，则点M，N分别是边AB，DC的中点，直线MN是矩形ABCD的一条对称轴.
由此得到矩形的轴对称性：
矩形是轴对称图形，过每一组对边中点的直线都是矩形的对称轴.
例2.如图，四边形ABCD 为矩形，试利用矩形的性质，说明：直角三角形ABC斜边AC上的中线BO等于斜边的一半.
证明 ∵ 四边形ABCD是矩形，
又 AC=BD，(矩形的对角线相等.)
3.矩形的一组邻边长分别是3cm和4cm则它的对角线长是______.
2.下面性质中，矩形不一定具有的是（ ） A.对角线相等 B.四个角相等 C.是轴对称图形 D.对角线互相垂直
4.矩形ABCD的对角线的长为2，∠BDC=300,则矩形ABCD的面积为______.
1.矩形具有而一般平行四边形不具有的性质是（ ） A、对角线相等 B、对边相等 C、对角相等 D、对角线互相平分
5.矩形两条对角线所夹的锐角为60°，较短的边长为3.6cm，则对角线的长为_____cm.
6.矩形ABCD中，AC、BD相交于点O，AB=6，BC=8，则△ABO的周长为_____
7.在Rt△ABC中，斜边AC上的中线和高分别是6cm和5cm，则Rt△ABC的面积是 。
8.已知矩形的一条对角线的长度为2cm，两条对角线的一个夹角为60°，则矩形的各边长是 .
变式：若BD=8cm，∠AOD=120°，求边AB的长。
10.如图，矩形ABCD中，AE平分∠BAD交BC于点E，ED=5cm，EC=3cm，求矩形的周长。
注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.
又AE平分∠BAD ∴BE=AB
矩形的周长=2(4+7)=22
11.矩形ABCD中，AB=2BC，AE=AB，求∠EBC的度数。
∵AE=AB， AB=2BC， AD=BC
∴∠AED=30°=∠EAB ，
∵AE=AB，∴∠AEB=75°=∠ABE ，
1.如图，矩形AEFG和矩形ADCB的大小、形状完全相同，把它们拼成如图所示的L型图案，已∠FAE=30°,分别求∠1、∠2的度数。
∠1=45 °,∠2=15 °
2.如图，已知矩形ABCD中，F是BC上一点，且AF=BC，DE⊥AF，垂足是E，连接DF．求证： （1）△ABF≌△DEA； （2）DF是∠EDC的平分线．
提示：（1）由AAS得证结论。
（2）由（1）得AB=DE=DC，DF=DFRt△DEF≌Rt△CDF；∠FDE=∠FDC