2022-2023学年北京市丰台区七年级（上）期末数学试卷

2022-2023学年北京市丰台区七年级（上）期末数学试卷

一、选择题（共30分，每题3分）第1—10题均有四个选项，符合题意的选项只有一个．

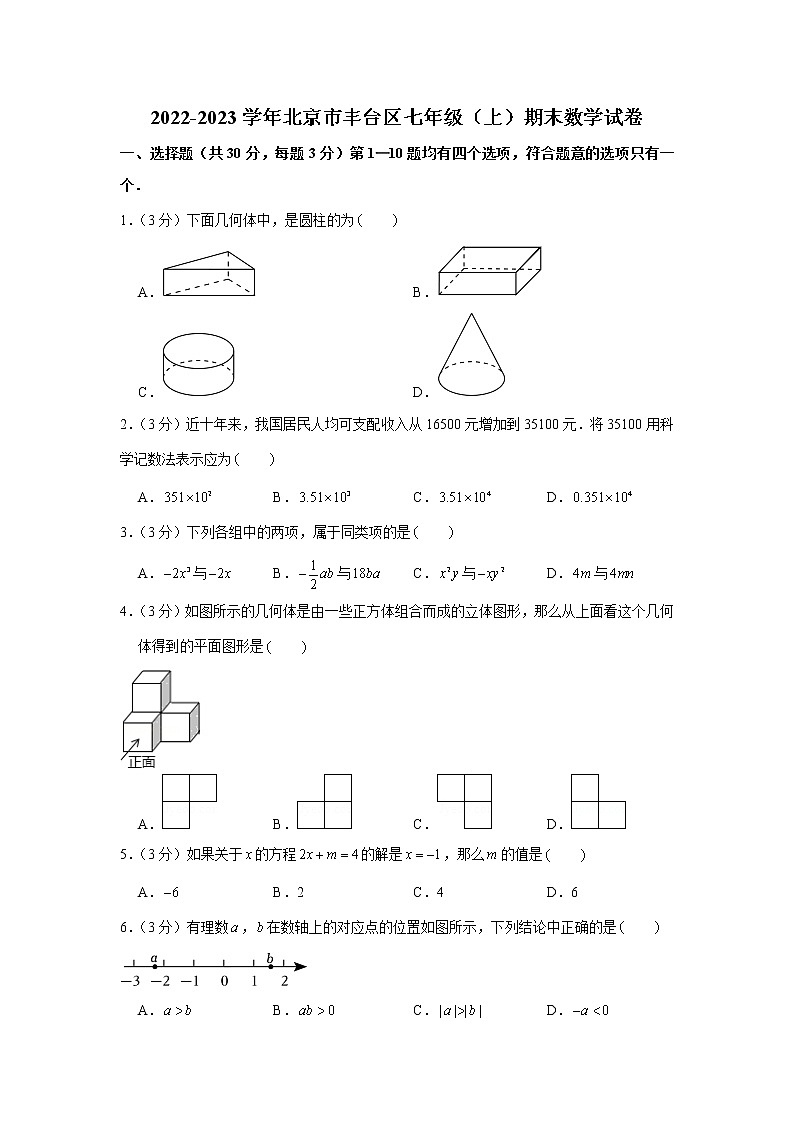
1．（3分）下面几何体中，是圆柱的为　　

A． B． 

C． D．

2．（3分）近十年来，我国居民人均可支配收入从16500元增加到35100元．将35100用科学记数法表示应为　　

A． B． C． D．

3．（3分）下列各组中的两项，属于同类项的是　　

A．与 B．与 C．与 D．与

4．（3分）如图所示的几何体是由一些正方体组合而成的立体图形，那么从上面看这个几何体得到的平面图形是　　

A． B． C． D．

5．（3分）如果关于的方程的解是，那么的值是　　

A． B．2 C．4 D．6

6．（3分）有理数，在数轴上的对应点的位置如图所示，下列结论中正确的是　　

A． B． C． D．

7．（3分）如图，点为线段的中点，点在线段上，如果，，那么线段的长是　　

A．2 B．3 C．4 D．5

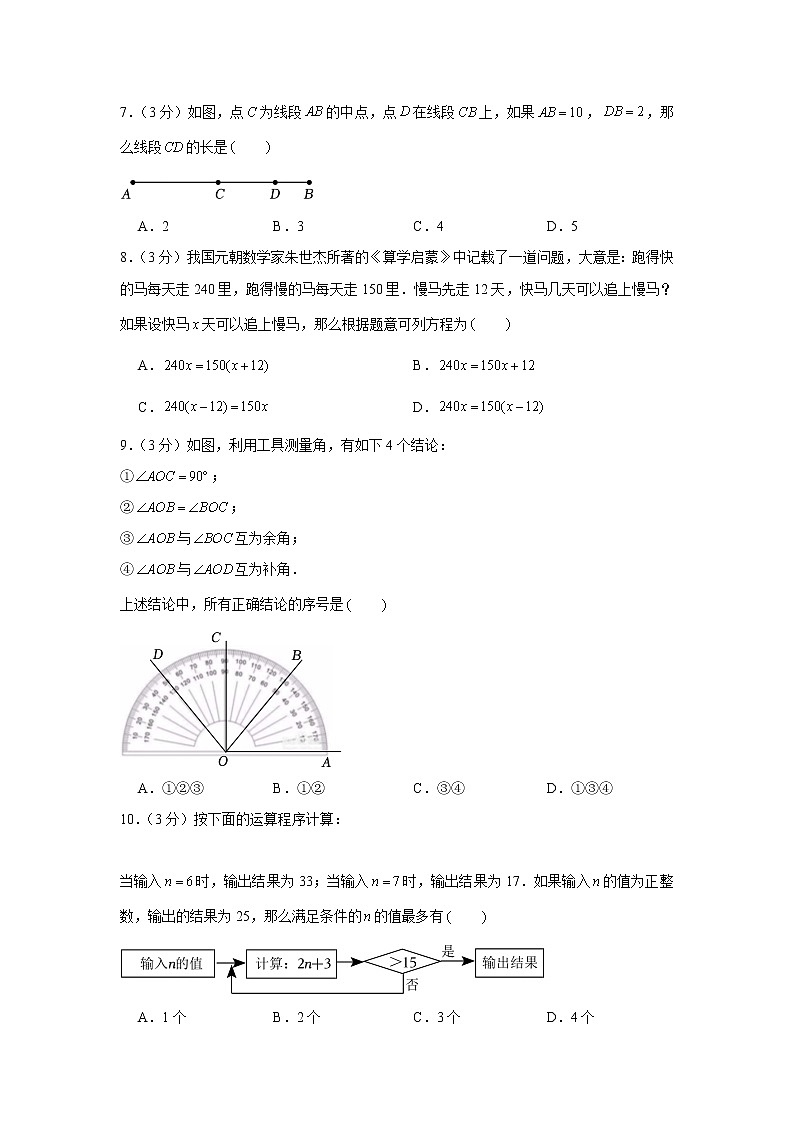
8．（3分）我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题，大意是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可以追上慢马？如果设快马天可以追上慢马，那么根据题意可列方程为　　

A． B． 

C． D．

9．（3分）如图，利用工具测量角，有如下4个结论：

①；

②；

③与互为余角；

④与互为补角．

上述结论中，所有正确结论的序号是　　

A．①②③ B．①② C．③④ D．①③④

10．（3分）按下面的运算程序计算：

当输入时，输出结果为33；当输入时，输出结果为17．如果输入的值为正整数，输出的结果为25，那么满足条件的的值最多有　　

A．1个 B．2个 C．3个 D．4个

二、填空题（共24分，每题3分）

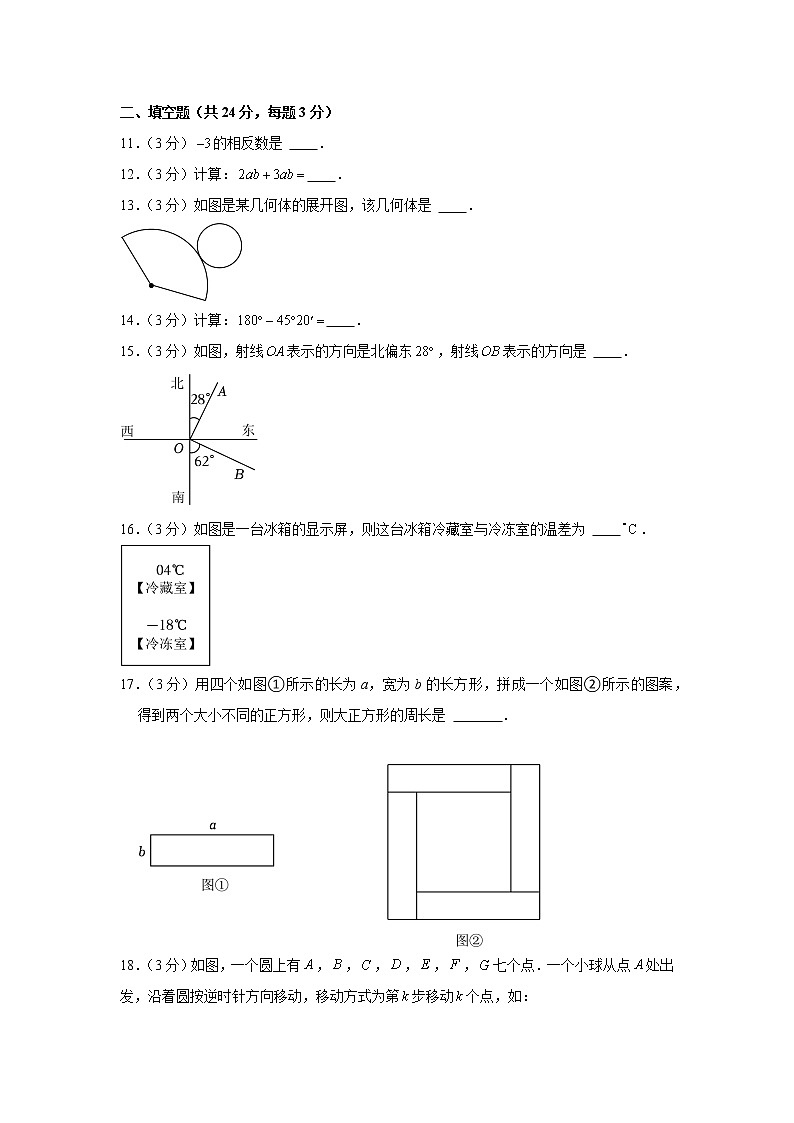
11．（3分）的相反数是 　　．

12．（3分）计算：　　．

13．（3分）如图是某几何体的展开图，该几何体是 　　．

14．（3分）计算：　　．

15．（3分）如图，射线表示的方向是北偏东，射线表示的方向是 　　．

16．（3分）如图是一台冰箱的显示屏，则这台冰箱冷藏室与冷冻室的温差为 　　．

17．（3分）用四个如图①所示的长为a，宽为b的长方形，拼成一个如图②所示的图案，得到两个大小不同的正方形，则大正方形的周长是 　   　．

18．（3分）如图，一个圆上有，，，，，，七个点．一个小球从点处出发，沿着圆按逆时针方向移动，移动方式为第步移动个点，如：

第1步，从点处移动至点处；

第2步，从点处移动至点处；

第3步，从点处移动至点处；

则第5步小球移动至点 　　处；

第100步小球移动至点 　　处．

三、解答题（共46分，第19题3分，第20-22题，每题4分，第23-27题，每题5分，第28题6分）解答应写出文字说明、演算步骤或证明过程。

19．（3分）计算：．

20．（4分）计算：．

21．（4分）解方程：．

22．（4分）解方程：．

23．（5分）先化简，再求值：，其中，．

24．（5分）如图，平面上有三个点，，．

（1）根据下列语句按要求画图．

①画直线，画射线，连接；

②用圆规在线段的延长线上截取，连接（保留作图痕迹）；

（2）　　（填“”“ ”或“” ，依据是 　　．

25．（5分）如图，是直线上一点，平分，，．求的度数．

补充完成下面的解答过程．

解：因为是直线上一点，

所以．

因为平分，

所以　　，

所以与互为余角．

因为，

所以 　　与 　　互为余角．

所以（依据是：　　．

因为，

所以　　．

26．（5分）某学校在七年级开展种植类的劳动课程．现需要购买仿生阳光房若干个．经调查发现，同一款式的仿生阳光房在甲、乙两家商店的标价均是100元．

新年将至，两家商店开展促销活动，优惠方式如下：

甲商店：每个仿生阳光房按9折（标价的出售；

乙商店：购买的仿生阳光房的个数不超过10时，按标价出售；购买的仿生阳光房的个数超过10时，超过部分按8折（标价的出售．

（1）若在甲商店购买10个该款式的仿生阳光房，则花费 　　元；

（2）若在乙商店购买个该款式的仿生阳光房，则花费 　　元（用含的代数式表示）；

（3）购买该款式的仿生阳光房的个数为多少时，在甲、乙两家商店的花费相同？

27．（5分）有这样一个问题：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和能被11整除吗？下面是小明的探究过程，请补充完整：

（1）举例：例①，；

例②，；

例③　　．

（2）说理：设一个两位数的十位上的数是，个位上的数是，

那么这个两位数可表示为 　　．

依题意得到的新数可表示为 　　．

通过计算说明这个两位数与得到的新数的和能否被11整除：　　．

（3）结论：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和 　　（填“能”或“不能” 被11整除．

28．（6分）在数轴上，点表示的数为0，点表示的数为．给出如下定义：对于该数轴上的一点与线段上一点，如果线段的长度有最大值，那么称这个最大值为点与线段的“闭距离”．如图1，若，点表示的数为3，当点与点重合时，线段的长最大，值是4，则点与线段的“闭距离”为4．

（1）如图2，在该数轴上，点表示的数为，点表示的数为2．

①当时，点与线段的“闭距离”为 　　；

②若点与线段的“闭距离”为3，求的值；

（2）在该数轴上，点表示的数为，点表示的数为，若线段上存在点，使得点与线段的“闭距离”为4，直接写出的最大值与最小值．

2022-2023学年北京市丰台区七年级（上）期末数学试卷

参考答案与试题解析

一、选择题（共30分，每题3分）第1—10题均有四个选项，符合题意的选项只有一个．

1．（3分）下面几何体中，是圆柱的为　　

A． B． 

C． D．

【解答】解：由图可知：是三棱柱，是四棱柱，是圆柱，是圆锥，

故选：．

2．（3分）近十年来，我国居民人均可支配收入从16500元增加到35100元．将35100用科学记数法表示应为　　

A． B． C． D．

【解答】解：．

故选：．

3．（3分）下列各组中的两项，属于同类项的是　　

A．与 B．与 C．与 D．与

【解答】解：．与所含字母相同，但相同字母的指数不相同，不是同类项，选项不符合题意；

．与所含字母相同，并且相同字母的指数也相同，是同类项，选项符合题意；

．与所含字母相同，但相同字母的指数不相同，不是同类项，选项不符合题意；

．与所含字母不相同，不是同类项，选项不符合题意；

故选：．

4．（3分）如图所示的几何体是由一些正方体组合而成的立体图形，那么从上面看这个几何体得到的平面图形是　　

A． B． C． D．

【解答】解：根据几何体可得此图形的俯视图从左往右有2列，正方形的个数依次为2，1．

故选：．

5．（3分）如果关于的方程的解是，那么的值是　　

A． B．2 C．4 D．6

【解答】解：将代入原方程得，

解得：，

的值为6．

故选：．

6．（3分）有理数，在数轴上的对应点的位置如图所示，下列结论中正确的是　　

A． B． C． D．

【解答】解：由数轴可知，，，

，，，，

故选项不符合题意，只有选项是符合题意．

故选：．

7．（3分）如图，点为线段的中点，点在线段上，如果，，那么线段的长是　　

A．2 B．3 C．4 D．5

【解答】解：，是的中点，

，

．

故选：．

8．（3分）我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题，大意是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可以追上慢马？如果设快马天可以追上慢马，那么根据题意可列方程为　　

A． B． 

C． D．

【解答】解：设快马天可以追上慢马，则此时慢马已出发天，

依题意，得：．

故选：．

9．（3分）如图，利用工具测量角，有如下4个结论：

①；

②；

③与互为余角；

④与互为补角．

上述结论中，所有正确结论的序号是　　

A．①②③ B．①② C．③④ D．①③④

【解答】解：①，故①正确；

②，，

，

故②不正确；

③，

与互为余角，

故③正确；

④，，

，

与互为补角，

故④正确；

所以，上述结论中，所有正确结论的序号是①③④，

故选：．

10．（3分）按下面的运算程序计算：

当输入时，输出结果为33；当输入时，输出结果为17．如果输入的值为正整数，输出的结果为25，那么满足条件的的值最多有　　

A．1个 B．2个 C．3个 D．4个

【解答】解：如果输入的值，一次运算就输出结果25，于是，解得；

如果输入的值，两次运算才能输出结果25，于是第1次运算输出的结果为11，再第1次输入的数满足，解得；

如果输入的值，三次运算才能输出结果25，于是第1次运算输出的结果为4，再第1次输入的数满足，解得不合题意舍去；

所以满足条件的的值最多由2个，

故选：．

二、填空题（共24分，每题3分）

11．（3分）的相反数是 　3　．

【解答】解：，

故的相反数是3．

故答案为：3．

12．（3分）计算：　　．

【解答】解：原式

．

故答案为：．

13．（3分）如图是某几何体的展开图，该几何体是 　圆锥　．

【解答】解：由题意知，该几何体是圆锥，

故答案为：圆锥．

14．（3分）计算：　　．

【解答】解：原式

，

故答案为：．

15．（3分）如图，射线表示的方向是北偏东，射线表示的方向是 　南偏东　．

【解答】解：根据方向角的定义可知，

射线表示的方向是北偏东，射线表示的方向是南偏东，

故答案为：南偏东．

16．（3分）如图是一台冰箱的显示屏，则这台冰箱冷藏室与冷冻室的温差为 　22　．

【解答】解：，

故答案为：22．

17．（3分）用四个如图①所示的长为a，宽为b的长方形，拼成一个如图②所示的图案，得到两个大小不同的正方形，则大正方形的周长是 　4a+4b　．

【解答】解：由题意可得，大正方形的边长为a+b，

∴大正方形的周长＝4（a+b）＝4a+4b，

故答案为：4a+4b．

18．（3分）如图，一个圆上有，，，，，，七个点．一个小球从点处出发，沿着圆按逆时针方向移动，移动方式为第步移动个点，如：

第1步，从点处移动至点处；

第2步，从点处移动至点处；

第3步，从点处移动至点处；

则第5步小球移动至点 　　处；

第100步小球移动至点 　　处．

【解答】解：由题意知，前1步移动的点数为1，

前2步移动的点数为，

前3步移动的点数为，

前4步移动的点数为，

前步移动的点数为，

前5步小球移动的点数为，

前100步小球移动的点数为，

由题意可知，当小球每移动1个点，2个点，3个点，4个点，5点点，6个点，7个点次到点、、、、、、处，

，，

第5步小球移动至点处；

第100步小球移动至点处．

故答案为：；．

三、解答题（共46分，第19题3分，第20-22题，每题4分，第23-27题，每题5分，第28题6分）解答应写出文字说明、演算步骤或证明过程。

19．（3分）计算：．

【解答】解：原式

．

20．（4分）计算：．

【解答】解：

．

21．（4分）解方程：．

【解答】解：，

，

，

，

．

22．（4分）解方程：．

【解答】解：，

去分母，得，

去括号，得，

移项，得，

合并同类项，得．

23．（5分）先化简，再求值：，其中，．

【解答】解：

；

当，时，

原式．

24．（5分）如图，平面上有三个点，，．

（1）根据下列语句按要求画图．

①画直线，画射线，连接；

②用圆规在线段的延长线上截取，连接（保留作图痕迹）；

（2）　　（填“”“ ”或“” ，依据是 　　．

【解答】解：（1）①如图，直线，射线，线段即为所求；

②如图，线段即为所求．

（2）．

故答案为：．两点之间线段最短．

25．（5分）如图，是直线上一点，平分，，．求的度数．

补充完成下面的解答过程．

解：因为是直线上一点，

所以．

因为平分，

所以　90　，

所以与互为余角．

因为，

所以 　　与 　　互为余角．

所以（依据是：　　．

因为，

所以　　．

【解答】解：是直线上一点，

．

平分，

，

与互为余角．

，

与互为余角．

（依据是：同角的余角相等）．

，

．

故答案为：90，，，同角的余角相等，30．

26．（5分）某学校在七年级开展种植类的劳动课程．现需要购买仿生阳光房若干个．经调查发现，同一款式的仿生阳光房在甲、乙两家商店的标价均是100元．

新年将至，两家商店开展促销活动，优惠方式如下：

甲商店：每个仿生阳光房按9折（标价的出售；

乙商店：购买的仿生阳光房的个数不超过10时，按标价出售；购买的仿生阳光房的个数超过10时，超过部分按8折（标价的出售．

（1）若在甲商店购买10个该款式的仿生阳光房，则花费 　900　元；

（2）若在乙商店购买个该款式的仿生阳光房，则花费 　　元（用含的代数式表示）；

（3）购买该款式的仿生阳光房的个数为多少时，在甲、乙两家商店的花费相同？

【解答】解：（1）（元，

在甲商店购买10个该款式的仿生阳光房需花费900元，

故答案为：900．

（2）元，

在乙商店购买个该款式的仿生阳光房需花费元，

故答案为：．

（3）当时，在甲、乙两家商店购买所需的费用不相等，

根据题意得，

解得，

答：购买该款式的仿生阳光房20个时，在甲、乙两家商店的花费相同．

27．（5分）有这样一个问题：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和能被11整除吗？下面是小明的探究过程，请补充完整：

（1）举例：例①，；

例②，；

例③　，　．

（2）说理：设一个两位数的十位上的数是，个位上的数是，

那么这个两位数可表示为 　　．

依题意得到的新数可表示为 　　．

通过计算说明这个两位数与得到的新数的和能否被11整除：　　．

（3）结论：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和 　　（填“能”或“不能” 被11整除．

【解答】解：（1），，（答案不唯一）

故答案为：，，（答案不唯一）

（2）十位数字是，个位数字是的两位数可表示为：，

交换后，十位数字是，个位数字是的两位数可表示为：，

这两个两位数的和为：，而，

所以这两个两位数的和能被11整除，

故答案为：，，，；

（3）由（1）（2）可知，

将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和能被11整除，

故答案为：能．

28．（6分）在数轴上，点表示的数为0，点表示的数为．给出如下定义：对于该数轴上的一点与线段上一点，如果线段的长度有最大值，那么称这个最大值为点与线段的“闭距离”．如图1，若，点表示的数为3，当点与点重合时，线段的长最大，值是4，则点与线段的“闭距离”为4．

（1）如图2，在该数轴上，点表示的数为，点表示的数为2．

①当时，点与线段的“闭距离”为 　2　；

②若点与线段的“闭距离”为3，求的值；

（2）在该数轴上，点表示的数为，点表示的数为，若线段上存在点，使得点与线段的“闭距离”为4，直接写出的最大值与最小值．

【解答】解：（1）①根据题意可知，时，到的最大值为的长，

，，

点与线段的“闭距离”为2，

故答案为：2；

②点到的“闭距离”为3，

当时，，

当时，，，

的值为或5；

（2）点表示的数为，点表示的数为，在线段上存在点，使得点与线段的“闭距离”为4，

当时，可得不等式组，

解得：，

当时，可得不等式组，

解得：，

综上所述，或，

的最大值为3，最小值为．