2020-2021学年重庆市江北区七年级（上）期末数学试卷

2020-2021学年重庆市江北区七年级（上）期末数学试卷

一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号

1．（4分）中国是世界上最早认识和应用负数的国家，比西方早一千多年，在我国古代著名的数学专著《九章算术》中，首次引入负数，如果收入100元记作元，则元表示　　

A．支出40元 B．收入40元 C．支出60元 D．收入60元

2．（4分）单项式的系数和次数分别是　　

A．，2 B．，2 C．，3 D．，3

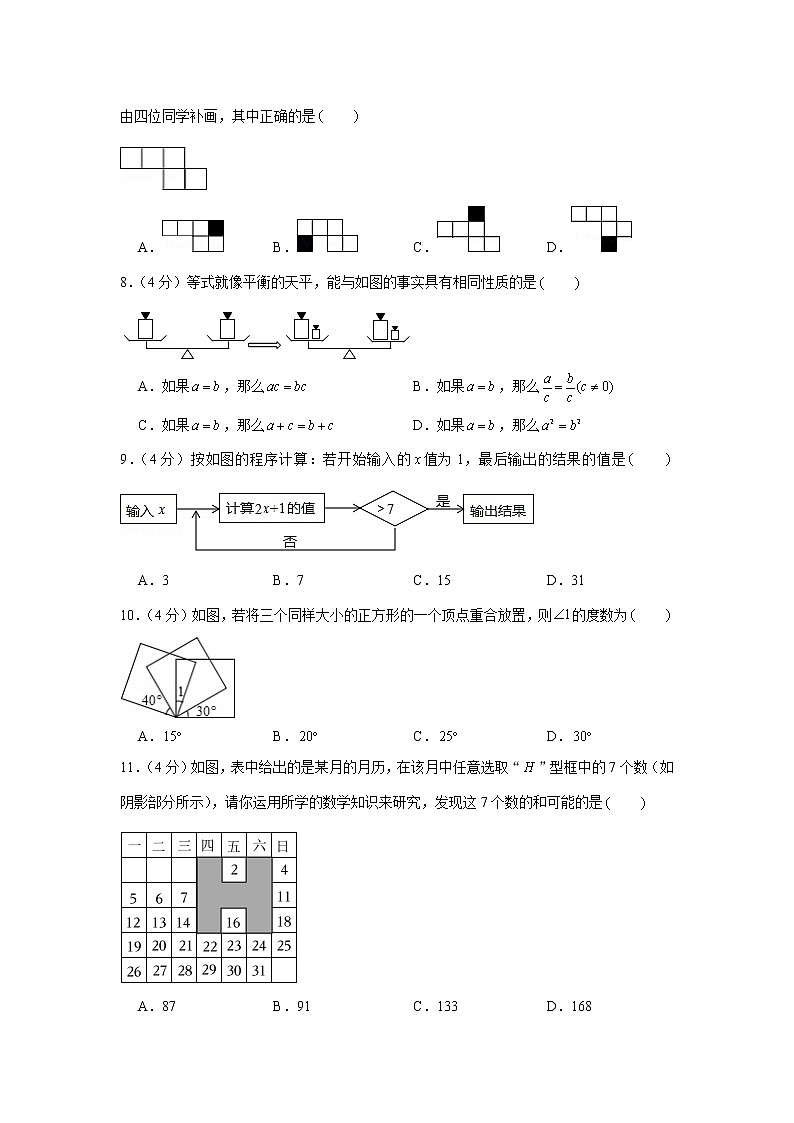
3．（4分）如图所示的长方形沿图中虚线旋转一周，能得到的几何体是　　

A． B． C． D．

4．（4分）下列方程是一元一次方程的为　　

A． B． C． D．

5．（4分）在数12、、0、、、中，负数有　　

A．2个 B．3个 C．4个 D．5个

6．（4分）下列说法正确的是　　

A．若，则点是线段的中点 

B．若，则直线是的平分线 

C．连接、的线段叫做、两点间的距离 

D．两点之间，线段最短

7．（4分）如图，它需再添一个面，折叠后才能围成一个正方体．图中的黑色小正方形分别由四位同学补画，其中正确的是　　

A． B． C． D．

8．（4分）等式就像平衡的天平，能与如图的事实具有相同性质的是　　

A．如果，那么 B．如果，那么 

C．如果，那么 D．如果，那么

9．（4分）按如图的程序计算：若开始输入的值为1，最后输出的结果的值是　　

A．3 B．7 C．15 D．31

10．（4分）如图，若将三个同样大小的正方形的一个顶点重合放置，则的度数为　　

A． B． C． D．

11．（4分）如图，表中给出的是某月的月历，在该月中任意选取“”型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现这7个数的和可能的是　　

A．87 B．91 C．133 D．168

12．（4分）已知数、、在数轴上的位置如图所示，满足，则下列各式：①；②；③：④正确的个数有　　个．

A．4 B．3 C．2 D．1

二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡

13．（4分）2020年11月1日日，天猫双十一全球狂欢季成交额4982亿，498200000000用科学记数法表示为 　　．

14．（4分）若与是同类项，则的值是 　　．

15．（4分）计算：　　．

16．（4分）某食堂购进10袋大米，每袋以50千克为标准，超过的记为正，不足的记为负，称重记录如下：

这10袋大米一共 　　千克（结果精确到1千克）．

17．（4分）已知、为定值，关于的方程，无论为何值，方程的解都是，则　　．

18．（4分）将正整数按图的规律排列：

表中数2在第二行、第一列，记为；数5记为；数14记为，根据这一规律，数2021应记为 　　．

三、解答题（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算

19．（10分）计算．

（1）；

（2）．

20．（10分）解方程．

（1）；

（2）．

21．（10分）点是线段的中点，，点将线段分为两部分，．

①求线段的长．

②点在线段上，若点距离点的长度为，求线段的长．

22．（10分）已知，．

（1）化简；

（2）当，，求的值．

23．（10分）某车间为提高生产总量，在原有16名工人的基础上，新调入若干名工人，使得调整后车间的总人数是调入工人人数的3倍多4人．

（1）调入多少名工人；

（2）在（1）的条件下，每名工人每天可以生产1200个螺柱或2000个螺母，1个螺柱需要2个螺母，为使每天生产的螺柱和螺母刚好配套，应该安排生产螺柱和螺母的工人各多少名？

24．（10分）若一个正整数，它的各位数字是左右对称的，则称这个数是对称数，如22，797，12321都是对称数，最小的对称数是11，没有最大的对称数，因为数位是无穷的．

（1）有一种产生对称数的方式是：将某些自然数与它的逆序数相加，得出的和再与和的逆序数相加，连续进行下去，便可得到一个对称数．如：17的逆序数为71，17+71＝88，88是一个对称数；687的逆序数为786，687+786＝1473，1473的逆序数为3741，1473+3741＝5214，5214的逆序数为4152，5214+4152＝9339，9339是一个对称数，请你根据以上材料，求以39产生的第一个对称数；

（2）若将一个三位对称数减去其各位数字之和，请你证明所得的结果能被9整除；

（3）将一个三位数的中间数去掉，成为一个两位数，且满足（如155＝9×15+4×5）．试求出所有这样的三位数，其中的三位对称数有几个？

25．（10分）滴滴快车为我们日常出行提供了极大的便利，某滴滴快车的收费标准为：

（1）小明某天早上因为起床较晚，打滴滴去学校共用时10分钟，付费19元，请求出小明家离学校的距离；

（2）周末，小红和小华分别从家打车去公园游玩，他们家离公园分别为15公里和18公里，结果所付车费一样，其中先到的一人乘车时间和在公园门口等待时间一样，且都等于另一人乘车时间的一半，求他们各自付了多少车费．

四.解答题（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤。

26．（8分）如图在数轴上点、表示的数分别为，，且满足．

（1）点表示的数为 　　；点表示的数为 　　；

（2）若在原点处放一挡板，一小球甲从点处以1个单位秒的速度向左运动；同时另一小球乙从点处以3个单位秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为（秒，

①当时，甲小球到原点的距离　　；乙小球到原点的距离　　；

当时，甲小球到原点的距离　　；乙小球到原点的距离　　；

②试探究：甲，乙两小球到原点的距离可能相等吗？若不能，请说明理由．若能，请直接写出甲，乙两小球到原点的距离相等时经历的时间．

2020-2021学年重庆市江北区七年级（上）期末数学试卷

参考答案与试题解析

一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号

1．（4分）中国是世界上最早认识和应用负数的国家，比西方早一千多年，在我国古代著名的数学专著《九章算术》中，首次引入负数，如果收入100元记作元，则元表示　　

A．支出40元 B．收入40元 C．支出60元 D．收入60元

【解答】解：

因为收入100元记作元，

所以收入记为“”，则支出就记为“”

因此，元表示支出60元．

故选：．

2．（4分）单项式的系数和次数分别是　　

A．，2 B．，2 C．，3 D．，3

【解答】解：单项式的系数和次数分别是，3．

故选：．

3．（4分）如图所示的长方形沿图中虚线旋转一周，能得到的几何体是　　

A． B． C． D．

【解答】解：易得该图形旋转后可得上下底面是平行且半径相同的2个圆，应为圆柱，

故选：．

4．（4分）下列方程是一元一次方程的为　　

A． B． C． D．

【解答】解：．方程是一元一次方程，选项符合题意；

．方程是二元一次方程，选项不符合题意；

．方程是一元二次方程，选项不符合题意；

．方程是分式方程，选项不符合题意．

故选：．

5．（4分）在数12、、0、、、中，负数有　　

A．2个 B．3个 C．4个 D．5个

【解答】解：，，，

因此，负数有，，，

故选：．

6．（4分）下列说法正确的是　　

A．若，则点是线段的中点 

B．若，则直线是的平分线 

C．连接、的线段叫做、两点间的距离 

D．两点之间，线段最短

【解答】解：、当三点不在同一直线上的时候，点不是的中点，故错误；

、当位于的内部时候，此结论成立，故错误；

、连接两点之间的线段的长度叫两点间的距离，故错误；

、两点之间线段最短，故正确．

故选：．

7．（4分）如图，它需再添一个面，折叠后才能围成一个正方体．图中的黑色小正方形分别由四位同学补画，其中正确的是　　

A． B． C． D．

【解答】解：、四个方格形成的“田”字的，不能组成正方体，错；

、出现“”字的，不能组成正方体，错；

、以横行上的方格从上往下看：选项组成正方体；

、有两个面重合，不能组成正方体，错．

故选：．

8．（4分）等式就像平衡的天平，能与如图的事实具有相同性质的是　　

A．如果，那么 B．如果，那么 

C．如果，那么 D．如果，那么

【解答】解：观察图形，是等式的两边都加，得到，利用等式性质1，所以成立．

故选：．

9．（4分）按如图的程序计算：若开始输入的值为1，最后输出的结果的值是　　

A．3 B．7 C．15 D．31

【解答】解：，；

，；

，，

，

输出结果为15，

故选：．

10．（4分）如图，若将三个同样大小的正方形的一个顶点重合放置，则的度数为　　

A． B． C． D．

【解答】解：

又

故选：．

11．（4分）如图，表中给出的是某月的月历，在该月中任意选取“”型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现这7个数的和可能的是　　

A．87 B．91 C．133 D．168

【解答】解：设“”型框中最中间的一个数为，则左边的三个数从上到下依次为，，，右边的三个数从上到下依次为，，，

所以这7个数的和为，

解方程得，不合题意舍去；

解方程得；

解方程得，不合题意舍去；

解方程得，不合题意舍去；

所以这7个数的和可能的是91．

故选：．

12．（4分）已知数、、在数轴上的位置如图所示，满足，则下列各式：①；②；③：④正确的个数有　　个．

A．4 B．3 C．2 D．1

【解答】解：，

①，故①正确；

②，故②错误；

③，故③正确：

④，，故④正确．

所以正确的个数有①③④，共3个．

故选：．

二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡

13．（4分）2020年11月1日日，天猫双十一全球狂欢季成交额4982亿，498200000000用科学记数法表示为 　　．

【解答】解：．

故答案为：．

14．（4分）若与是同类项，则的值是 　4　．

【解答】解：与是同类项，

，，

解得，，

．

故答案为：4．

15．（4分）计算：　　．

【解答】解：，

故．

故答案为：．

16．（4分）某食堂购进10袋大米，每袋以50千克为标准，超过的记为正，不足的记为负，称重记录如下：

这10袋大米一共 　504　千克（结果精确到1千克）．

【解答】解：

（千克），

故答案为：504．

17．（4分）已知、为定值，关于的方程，无论为何值，方程的解都是，则　　．

【解答】解：把代入方程，得，

，

，

无论为何值，方程的解都是，

，，

解得，．

则．

故答案为：．

18．（4分）将正整数按图的规律排列：

表中数2在第二行、第一列，记为；数5记为；数14记为，根据这一规律，数2021应记为 　　．

【解答】解：观察发现，第一行的第2、4、6列的数分别为4、16、36，为所在列数的平方，然后向下每一行递减1至与列数相同的行止；

第一列的第1、3、5行的数分别为1、9、25，为所在行数的平方，然后向右每一列递减1至与列数相同的行止．

，，

所在的位置是第45行第5列，

即．

故答案为：．

三、解答题（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算

19．（10分）计算．

（1）；

（2）．

【解答】解：（1）；

；

（2）

．

20．（10分）解方程．

（1）；

（2）．

【解答】解：（1）去分母得，，

去括号得，，

移项得，，

合并同类项得，，

的系数化为1得，；

（2）去分母得，

去括号得，，

移项得，，

合并同类项得，，

的系数化为1得，．

21．（10分）点是线段的中点，，点将线段分为两部分，．

①求线段的长．

②点在线段上，若点距离点的长度为，求线段的长．

【解答】解：①点是线段的中点，，

，

．

，

；

②如图1，当点在点的左边时，

，

如图2，当点在点的右边时，

．

综上，或．

22．（10分）已知，．

（1）化简；

（2）当，，求的值．

【解答】解：（1）

；

（2）由（1）得，因为，，

所以．

23．（10分）某车间为提高生产总量，在原有16名工人的基础上，新调入若干名工人，使得调整后车间的总人数是调入工人人数的3倍多4人．

（1）调入多少名工人；

（2）在（1）的条件下，每名工人每天可以生产1200个螺柱或2000个螺母，1个螺柱需要2个螺母，为使每天生产的螺柱和螺母刚好配套，应该安排生产螺柱和螺母的工人各多少名？

【解答】解：（1）设调入名工人，

根据题意得：，

解得：，

则调入6名工人；

（2）（人，

设名工人生产螺柱，

根据题意得：，

解得：，

（人，

则10名工人生产螺柱，12名工人生产螺母．

24．（10分）若一个正整数，它的各位数字是左右对称的，则称这个数是对称数，如22，797，12321都是对称数，最小的对称数是11，没有最大的对称数，因为数位是无穷的．

（1）有一种产生对称数的方式是：将某些自然数与它的逆序数相加，得出的和再与和的逆序数相加，连续进行下去，便可得到一个对称数．如：17的逆序数为71，17+71＝88，88是一个对称数；687的逆序数为786，687+786＝1473，1473的逆序数为3741，1473+3741＝5214，5214的逆序数为4152，5214+4152＝9339，9339是一个对称数，请你根据以上材料，求以39产生的第一个对称数；

（2）若将一个三位对称数减去其各位数字之和，请你证明所得的结果能被9整除；

（3）将一个三位数的中间数去掉，成为一个两位数，且满足（如155＝9×15+4×5）．试求出所有这样的三位数，其中的三位对称数有几个？

【解答】（1）解：∵39的逆序数为93，39+93＝132，132的逆序数为231，132+231＝363，363是一个对称数，

∴以39产生的第一个对称数是363；

（2）证明：设三位对称数的百位数字是m，十位数字是n，则个位数字是m，这个三位数是100m+10n+m，其中m，n是整数，且1≤m≤9，0≤n≤9，

∵100m+10n+m﹣（m+n+m）

＝99m+9n

＝9（11m+n），

∵m，n是整数，且1≤m≤9，0≤n≤9，

∴9（11m+n）能被9整除，

∴将一个三位对称数减去其各位数字之和，所得的结果能被9整除；

（3）解：＝100a+10b+c，＝10a+c，

根据题意得：100a+10b+c＝9（10a+c）+4c，

化简得，5（a+b）＝6c，

∵1≤a≤9、0≤b≤9、0≤c≤9，且a，b，c为整数，

又5是质数，

∴，

∴或或或或或，

∴所有这样的三位数有155，245，335，425，515，605，而515是三位对称数，故其中的三位对称数有1个．

25．（10分）滴滴快车为我们日常出行提供了极大的便利，某滴滴快车的收费标准为：

（1）小明某天早上因为起床较晚，打滴滴去学校共用时10分钟，付费19元，请求出小明家离学校的距离；

（2）周末，小红和小华分别从家打车去公园游玩，他们家离公园分别为15公里和18公里，结果所付车费一样，其中先到的一人乘车时间和在公园门口等待时间一样，且都等于另一人乘车时间的一半，求他们各自付了多少车费．

【解答】解：（1）行车16公里的里程费为（元，

小明家离学校的距离小于16公里，

设小明家离学校的距离是公里，根据题意得：

，

解得，

答：小明家离学校的距离4公里；

（2）设先到的一人乘车时间是分钟，则另一人乘车时间是分钟，

若小红先到，则，

解得（不符合题意，舍去），

若小华先到，则，

解得，

，

答：他们各自付了53元车费．

四.解答题（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤。

26．（8分）如图在数轴上点、表示的数分别为，，且满足．

（1）点表示的数为 　　；点表示的数为 　　；

（2）若在原点处放一挡板，一小球甲从点处以1个单位秒的速度向左运动；同时另一小球乙从点处以3个单位秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为（秒，

①当时，甲小球到原点的距离　　；乙小球到原点的距离　　；

当时，甲小球到原点的距离　　；乙小球到原点的距离　　；

②试探究：甲，乙两小球到原点的距离可能相等吗？若不能，请说明理由．若能，请直接写出甲，乙两小球到原点的距离相等时经历的时间．

【解答】解：（1），，，

，，

，，

点表示的数为，点表示的数为6；

故答案为：；6；

（2）①当时，甲小球到原点的距离，乙小球到原点的距离；

当时，甲小球到原点的距离；乙小球到原点的距离，

故答案为：3；3；5；3；

②甲，乙两小球到原点的距离能相等，理由：

设运动的时间为（秒，

当小球乙未到达挡板前，由题意得：

，

解得：；

当小球乙到达挡板后，由题意得：

，

解得：，

综上，甲，乙两小球到原点的距离相等时经历的时间为1秒或4秒．