【新高考】2023年高考数学二轮复习精讲精练学案——第14讲 解三角形（原卷版+解析版）

这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第14讲 解三角形（原卷版+解析版），文件包含第十四讲解三角形解析版docx、第十四讲解三角形原卷版docx等2份学案配套教学资源，其中学案共37页， 欢迎下载使用。

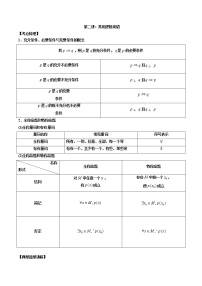
正弦定理
在中，(为外接圆半径).
变形形式：（1）
余弦定理
①；②；③。
推论：①；②；③
三角形面积公式

重要结论
在中，分别为角的对边，.
（2）内角和定理：
= 1 \* GB3 \* MERGEFORMAT ①
同理有：，.
= 2 \* GB3 \* MERGEFORMAT ②；
= 3 \* GB3 \* MERGEFORMAT ③斜三角形中，
= 4 \* GB3 \* MERGEFORMAT ④；
= 5 \* GB3 \* MERGEFORMAT ⑤在中，内角成等差数列.
【典型题型讲解】
考点一：正、余弦定理
【典例例题】
例1．（2022·广东揭阳·高三期末）在中，角所对的边分别为，且.
(1)求角；
(2)若，且的面积为，且，求和的值.
例2．（2022·广东·铁一中学高三期末）在①，②，③这三个条件中任选一个，补充在下面的横线上，并加以解答.
已知的内角，，所对的边分别是，，，若______.
（1）求角；
（2）若，求周长的最小值，并求出此时的面积.
【方法技巧与总结】
在解三角形题目中，若已知条件同时含有边和角，但不能直接使用正弦定理或余弦定理得到答案，要选择“边化角”或“角化边”，变换原则常用：
（1）若式子含有的齐次式，优先考虑正弦定理，“角化边”；
（2）若式子含有的齐次式，优先考虑正弦定理，“边化角”；
（3）若式子含有的齐次式，优先考虑余弦定理，“角化边”；
（4）代数变形或者三角恒等变换前置；
（5）含有面积公式的问题，要考虑结合余弦定理使用；
（6）同时出现两个自由角（或三个自由角）时，要用到.
【变式训练】
1．（2022·广东东莞·高三期末）的内角、、的对边分别为、、，已知.
(1)求；
(2)若，的面积为，求的周长.
2．（2022·广东汕尾·高三期末）中，内角A，B，C所对的边分别为a，b，c，且
(1)求角B
(2)当b=3时，求的面积的最大值．
3．（2022·广东惠州·一模）在△ABC中，内角A，B，C所对的边分别为a，b，c，，且.
(1)求证：；
(2)当时，求.
4．（2022·广东·一模）在中，角的对边分别为，下面给出有关的三个论断：①；②；③.
化简上述三个论断，求出角的值或角的关系，并以其中两个论断作为条件，余下的一个论断作为结论，写出所有可能的真命题.（不必证明）
论断①：；论断②：或；论断③：；所有可能的真命题有：①③②和①②③.
5．（2022·广东湛江·一模）已知在中，角A，B，C的对边分别为a，b，c，.
(1)求角A的大小；
(2)若，求周长的最大值.
6．（2022·广东广州·一模）△的内角A，B，C的对边分别为a，b，c，已知△的面积为.
(1)证明：；
(2)若，求.
7．（2022·广东汕头·一模）在①；②的面积为；③这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c的值；若问题中的三角形不存在，说明理由.问题：是否存在中，a，b，c分别为内角A，B，C的对边，，， ______？.
考点二：正弦、余弦定理在几何中的应用
【典例例题】
例1．（2022·广东佛山·高三期末）中，内角A，B，C所对的边分别为a，b，c，且.
(1)求角A的大小；
(2)若边上的中线，求的面积.
例2．（2022·广东汕头·高三期末）在△ABC中，角A，B，C所对的边分别a，b，c．已知2bcsB=ccsA+acsC．
(1)求B；
(2)若a=2，，设D为CB延长线上一点，且AD⊥AC，求线段BD的长．
例3．（2022·广东珠海·高三期末）在中，角A，B，C所对的边分别为a，b，c，且．
(1)求B；
(2)已知，D为边上的一点，若，，求的长．
【方法技巧与总结】
利用平面向量的有关知识如向量数量积将向量问题转化为三角函数形式，再利用三角函数转化求解.
【变式训练】
1．（2022·广东中山·高三期末）在中，内角A，B，C的对边分别为a，b，c，且．
（1）求A；
（2）如图，已知，D为的中点，点P在上，且满足，求的面积．
2．（2022·广东·金山中学高三期末）如图，在平面四边形中，，，.
(1)若，求的面积；
(2)若，，求.
3．（2022·广东清远·高三期末）在平面四边形中，．
(1)求；
(2)求的面积．
4.如图，在中，对边分别为，且.
(1)求角的大小；
(2)已知，若为外接圆劣弧上一点，且，求四边形的面积.
5．（2022·广东梅州·二模）在中，点在上，平分，已知，，
(1)求的长；
(2)求的值.
6．（2022·广东广州·二模）在平面四边形中，．
(1)求的面积；
(2)若，求的值；
【巩固练习】
一、单选题
1．记的内角A，B，C的对边分别为a，b，c，，,，则的值为（ ）
A．B．C．D．
2．在△ABC中，内角A，B，C所对的边分别为a，b，c，且，则的值为（ ）
A．4B．5C．6D．7
3．（2022·黑龙江·哈九中模拟预测（理））记的内角A，B，C的对边分别为a，b，c，，，．则的值为（ ）
A． B． C．D．
4．（2022·北京昌平·二模）在△中，只需添加一个条件，即可使△存在且唯一.条件：①； ②；③中，所有可以选择的条件的序号为（ ）
A．①B．①②C．②③D．①②③
二、多选题
5．（2022·全国·高三专题练习）内角，，的对边分别为，，.已知，且，则下列结论正确的是（ ）
A．B．
C．的周长为D．的面积为
6．（2022·河北·石家庄二中模拟预测）已知中，为外接圆的圆心，为内切圆的圆心，则下列叙述正确的是（ ）
A．外接圆半径为B．内切圆半径为
C．D．
三、填空题
7．（2022·河北·高三期中）已知中角A，B，C所对的边分别为a，b，c，，则的面积，该公式称作海伦公式，最早由古希腊数学家阿基米德得出．若的周长为15，，则的面积为___________________．
8．在△中，角A，B，C的对边分别为a，b，c，满足，，则___________．
四、解答题
9．已知在三角形中，，三角形的面积．
(1)若，求；
(2)若，求．
10．在中，角A，B，C所对的边分别为a，b，c，且．
(1)求角A的大小；
(2)若，的面积为4，求BC边上的高．
11．在中．．
(1)求角；
(2)若，点是线段的中点，于点，且，求的长．
12．已知对任意，，都有：，若的内角A、B、C的对边分别为a、b、c.，且.
(1)求c；
(2)若，过点C作，垂足为H，若，求的面积S.