【新高考】2023年高考数学二轮复习精讲精练学案——第13讲 三角函数图象及性质（原卷版+解析版）

这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第13讲 三角函数图象及性质（原卷版+解析版），文件包含第十三讲三角函数图象及性质解析版docx、第十三讲三角函数图象及性质原卷版docx等2份学案配套教学资源，其中学案共39页， 欢迎下载使用。

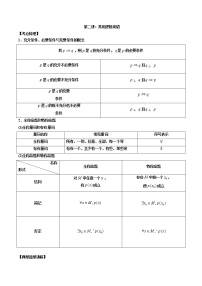
1、用五点法作正弦函数和余弦函数的简图
(1)在正弦函数，的图象中，五个关键点是：．
(2)在余弦函数，的图象中，五个关键点是：．
2、的图象与性质
（1）最小正周期：.
（2）定义域与值域：的定义域为R，值域为[-A,A].
（3）最值（）.
对于，
（4）对称轴与对称中心.（）
对于，
（5）单调性.（）
对于，
（6）平移与伸缩
由的图象变换得到(，)的图象的两种方法
(1)先平移后伸缩 (2)先伸缩后平移
【典型题型讲解】
考点一：三角函数的性质
【典例例题】
例1．（多选）（2022·广东汕头·高三期末）对于函数，x∈R，则（ ）
A．f(x)的最大值为1B．直线为其对称轴
C．f(x)在上单调递增D．点为其对称中心
例2．（2022·广东珠海·高三期末）关于函数，下列说法正确的是（ ）
A．函数的图象可由函数的图象向左平移个单位得到
B．的图象关于直线对称
C．的表达式可以改写为
D．若函数在的值域为，则m的取值范围是
【方法技巧与总结】
研究三角函数的性质，关键式将函数化为与
的形式利用正余弦函数与复合函数的性质求解.
【变式训练】
1．（2022·广东揭阳·高三期末）已知函数，则该函数的增区间为（ ）
A． B．
C． D．
2.（2022·广东茂名·一模）函数在区间上的最大值为______
3.已知函数，则下列说法正确的是（ ）
A．为奇函数B．为偶函数
C．为奇函数D．为偶函数
4.设函数，若时，的最小值为，则（ ）
A．函数的周期为
B．将函数的图象向左平移个单位，得到的函数为奇函数
C．当，的值域为
D．函数在区间上的零点个数共有6个
5．设函数，，其中，.若，，且的最小正周期大于，则（ ）
A．，B．，
C．，D．，
6.若函数，，，又，，且的最小值为，则的值为（ ）
A．B．C．4D．
7.（2022·广东湛江·一模）已知函数，，，且在区间上有且只有一个极大值点，则的最大值为___________.
8．（2021·广东佛山·一模）已知函数.从下面的两个条件中任选其中一个：①；②若，且的最小值为，，求解下列问题：
(1)化简的表达式并求的单调递增区间；
(2)已知，求的值.
考点二：三角函数的图象
【典例例题】
例1．（2022·广东·金山中学高三期末）为了得到函数的图象，可以将函数的图象（ ）
A．向右平移个单位长度B．向右平移个单位长度
C．向左平移个单位长度D．向左平移个单位长度
例2．（多选）（2022·广东中山·高三期末）已知函数的部分图象如图所示，下列说法正确的是（ ）
A．函数的图象关于点对称 B．函数的图象关于直线对称
C．函数在上单调递减
D．函数图象向右平移个单位可得函数的图象
【方法技巧与总结】
1.图象变换过程中务必分清式相位变换，还是周期变换.变换只是相对于其中的自变量而言的，如果的系数不是1，就要把这个系数提取后再确定变换的单位长度和方向.
2.已知函数的图象求解析式时，常采用待定系数法，由图中的最高点、最低点或特殊点求A；由函数的周期确定；确定常根据“五点法”中的五个点求解，其中一般把第一个零点作为突破口，可以从图象的升降找准第一个零点的位置.
【变式训练】
1．（2022·广东广东·一模）将正弦函数图象上各点的横坐标缩短为原来的，纵坐标不变，得到函数的图象．则图象的一个对称中心为（ ）
A．B．C．D．
2．（2022·广东韶关·一模）若将函数的图象向左平移个单位长度，则平移后的函数图象的一条对称轴为（ ）
A． B． C．D．
3．（2022·广东广州·一模）将函数的图象向右平移个单位，得到函数的图象，则下列说法正确的是（ ）
A．若，则是偶函数 B．若，则在区间上单调递减
C．若，则的图象关于点对称 D．若，则在区间上单调递增
4．(多选)（2022·广东·铁一中学高三期末）将函数的图象向右平移个单位长度后得到函数的图象，且，则下列说法正确的是（ ）
A．为奇函数 B．
C．当时，在上有4个极值点 D．若在上单调递增，则的最大值为5
5．(多选)（2022·广东东莞·高三期末）已知函数，若且对任意都有，则下列结论正确的是（ ）
A． B．
C．的图象向左平移个单位后，图象关于原点对称
D．的图象向右平移个单位后，图象关于轴对称
6．（多选）（2022·广东清远·高三期末）将函数图象上所有的点向右平移个单位长度后，得到函数的图象，若函数，则（ ）
A．的最小值是 B．的图象关于直线对称
C．的最小正周期是 D．的单调递增区间是
7．（多选）（2022·广东惠州·一模）已知函数（其中，，）的部分图象如图所示，则下列结论正确的是（ ）
A．函数的图象关于直线对称 B．函数的图象关于点对称
C．函数在区间上单调递增
D．与图象的所有交点的横坐标之和为
9．（2022·广东茂名·二模）已知函数 的部分图象如图所示．将函数的图象向左平移 个单位得到 的图象，则（ ）
A． ）B．
C． D．
10．（2022·广东惠州·二模）已知函数的部分图象如图所示，则下列结论中正确的是（ ）
A．的最小正周期为B．
C．在上单调递增D．为奇函数
【巩固练习】
一、单选题
1．已知直线是函数的图象的一条对称轴，为了得到函数的图象，可把函数的图象（ ）
A．向左平移个单位长度B．向右平移个单位长度
C．向左平移个单位长度D．向右平移个单位长度
2．已知函数，若，则（ ）
A．B．2C．5D．7
3．已知函数，则下列结论错误的是（ ）
A．函数的最小正周期是 B．函数在区间上单调递减
C．函数的图象可由函数的图象向左平移个单位长度，再向下平移1个单位长度得到
D．函数的图象关于对称
4．如图是函数的图象的一部分，则要得到该函数的图象，只需要将函数的图象（ ）
A．向左平移个单位长度B．向右平移个单位长度
C．向左平移个单位长度D．向右平移个单位长度
二、多选题
5．已知函数，则下列说法正确的是（ ）
A．直线为函数f(x)图象的一条对称轴
B．函数f(x)图象横坐标缩短为原来的一半，再向左平移后得到
C．函数f(x)在[－，]上单调递增
D．函数的值域为[－2，]
6．设函数，则下列结论中正确的是（ ）
A．的图象关于点对称B．的图象关于直线对称
C．在上单调递减D．在上的最小值为0
7．已知函数，则下列说法正确的是（ ）
A． B．的图象关于原点对称
C．若，则 D．对，，，有成立
三、填空题
8．写出一个同时具有下列性质①②③的函数___________；已知函数满足：①；②；③函数在上单调递减；
9．已知函数的部分图象如图所示，则________．
10．已知函数，若，且在上有最大值，没有最小值，则的最大值为______．
四、解答题
11．已知函数
(1)求的值；
(2)求函数在上的增区间和值域．
12．设内角A，B，C的对边分别为a，b，c，函数．
(1)若，求的面积；
(2)当时，取最大值，求在上的值域.
14．已知函数，从下面两个条件：条件①、条件②中选择一个作为已知．
(1)求时函数的值域；
(2)若函数图象向右平移m个单位长度后与函数的图象重合，求正数m的最小值．
15．已知函数的部分图象如图所示．
(1)求函数的解析式；
(2)将函数的图象上所有的点向右平移个单位，再将所得图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数的图象．当时，方程恰有三个不相等的实数根，求实数a的取值范围和的值．
16．设.
(1)若，求使函数为偶函数；
(2)在（1）成立的条件下，当，求的取值范围.
17．（已知函数．
(1)求函数的最小正周期及单调递增区间；
(2)若函数关于点中心对称，求在上的值域．