【新高考】2023年高考数学二轮复习精讲精练学案——第05讲 函数的单调性、奇偶性、周期性讲义（原卷版+解析版）

这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第05讲 函数的单调性、奇偶性、周期性讲义（原卷版+解析版），文件包含第五讲函数的单调性奇偶性周期性讲义解析版docx、第五讲函数的单调性奇偶性周期性讲义原卷版docx等2份学案配套教学资源，其中学案共34页， 欢迎下载使用。

1．增函数与减函数
一般地，设函数的定义域为：
(1)如果对于定义域内某个区间上的任意两个自变量的值，，当时，都有，那么就说函数在区间上是增函数．
(2)如果对于定义域内某个区间上的任意两个自变量的值，，当时，都有，那么就说函数在区间上是减函数．
2．函数的最大值与最小值
一般地，设函数的定义域为，如果存在实数满足：
(1)对于任意的，都有；存在，使得，那么，我们称是函数的最大值．
(2)对于任意的，都有；存在，使得，那么我们称是函数的最小值．
3．函数单调性的两个等价结论
设则
(1)(或在上单调递增。
(2)(或⇔f(x)在上单调递减．
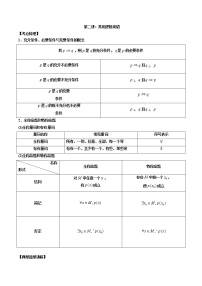
4．函数的奇偶性
5.奇偶函数的性质
(1)奇函数在关于原点对称的区间上的单调性相同，偶函数在关于原点对称的区间上的单调性相反．
(2)在公共定义域内
(ⅰ)两个奇函数的和函数是奇函数，两个奇函数的积函数是偶函数.
(ⅱ)两个偶函数的和函数、积函数是偶函数.
(ⅲ)一个奇函数与一个偶函数的积函数是奇函数.
(3)若是奇函数且处有意义，则.
6．函数的周期性
(1)周期函数：对于函数，如果存在一个非零常数，使得当取定义域内的任何值时，都有，那么就称函数为周期函数，称为这个函数的周期．
(2)最小正周期：如果在周期函数的所有周期中存在一个最小的正数，那么这个最小正数就叫做的最小正周期．
(3)常见结论：若，则；若，则；若，则.
【典型题型讲解】
考点一：函数的单调性
【典例例题】
例1.若定义在R上的函数f(x)对任意两个不相等的实数a，b，总有>0成立，则必有（ ）
A．f(x)在R上是增函数B．f(x)在R上是减函数
C．函数f(x)先增后减D．函数f(x)先减后增
【方法技巧与总结】
函数单调性的判断方法
①定义法：根据增函数、减函数的定义，按照“取值—变形—判断符号—下结论”进行判断．
②图象法：就是画出函数的图象，根据图象的上升或下降趋势，判断函数的单调性．
③直接法：就是对我们所熟悉的函数，如一次函数、二次函数、反比例函数等，直接写出它们的单调区间．
【变式训练】
1.已知函数，若，则实数的取值范围是___.
2.已知函数的定义域为，且对任意两个不相等的实数，都有，则不等式的解集为（ ）．
A．B．C．D．
3．（2022·广东惠州·一模）已知，则当时，与的大小关系是（ ）
A． B． C． D．不确定
4.“”是“函数是在上的单调函数”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
5．已知函数若，，，且仅有1个零点，则实数m的取值范围为（ ）
A．B．C．D．
6．若函数是上的单调函数，则的取值范围（ ）
A．B．C．D．
考点二：判断函数的奇偶性
【典例例题】
例1.已知函数，则（ ）
A．是偶函数，且在是单调递增B．是奇函数，且在是单调递增
C．是偶函数，且在是单调递减D．是奇函数，且在是单调递减
【方法技巧与总结】
函数的奇偶性的判断：图像法、解析式法；
常见函数的奇偶性。
【变式训练】
1．下列函数中，在其定义域内既是奇函数又是减函数的是（ ）
A．B．C．D．
2．（2022·广东·二模）存在函数使得对于都有，则函数可能为（ ）
A．B．C．D．
3．（2022·广东湛江·一模）下列函数是奇函数，且函数值恒小于1的是（ ）
A．B．
C．D．
4．（2022·广东广东·一模）下列四个函数中，以为周期且在上单调递增的偶函数有（ ）
A．B．
C．D．
考点三：函数的奇偶性的应用
【典例例题】
例1．（2022·广东中山·高三期末）（多选）已知函数，则下列说法正确的是（ ）
A．函数是偶函数B．函数是奇函数
C．函数在上为增函数D．函数的值域为
例2．（2022·广东汕尾·高三期末）我国著名数学家华罗庚先生曾说：数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休，在数学的学习和研究中，函数的解析式常用来研究函数图象的特征，函数的图象大致为（ ）
A．B．
C．D．
【方法技巧与总结】
函数单调性与奇偶性结合时，注意函数单调性和奇偶性的定义，以及奇偶函数图像的对称性.
【变式训练】
1.（2021·广东汕头·高三期末）已知偶函数f(x)在区间上单调递减，若f(-1)=0，则满足f(m)>0的实数m的取值范围是______．
2．（2022·广东·金山中学高三期末）已知函数，则________．
3．（2022·广东深圳·一模）已知函数是定义域为R的奇函数，当时，，则_________．
4．（2022·广东韶关·一模）已知函数是定义在上的奇函数，当时，，则
5．（2022·广东·一模）已知函数，，则图象如图的函数可能是( )
A．B．C．D．
6．（2022·广东湛江·一模）下列函数是奇函数，且函数值恒小于1的是（ ）
A．B．
C．D．
7．（2022·广东广州·一模）若函数的大致图象如图，则的解析式可能是( )
B．C．D．
8．（2022·广东广东·一模）函数的部分图象大致为（ ）
A．B．
C．D．
考点四：函数的对称性和周期性
【典例例题】
例1．设函数的定义域为D，若对任意的，且，恒有，则称函数具有对称性，其中点为函数的对称中心，研究函数的对称中心，求（ ）
A．2022B．4043C．4044D．8086
【方法技巧与总结】
（1）若函数有两条对称轴，，则函数是周期函数，且；
（2）若函数的图象有两个对称中心，则函数是周期函数，且；
（3）若函数有一条对称轴和一个对称中心，则函数是周期函数，且.
【变式训练】
1．（2022·广东珠海·高三期末）已知是定义域在上的奇函数，且满足．当时，，则（ ）
A．B．C．4D．
2．已知定义在R上的函数满足，且是奇函数，则（ ）
A．是偶函数B．的图象关于直线对称
C．是奇函数D．的图象关于点对称
3．已知函数的定义域为R，且对任意恒成立，又函数的图象关于点对称，且，则（ ）
A．2021B．C．2022D．
4．已知定义在R上的偶函数满足，且当时，，则下面结论正确的是（ ）
A．B．
C．D．
5．已知函数满足对任意恒成立，又函数的图象关于点对称，且 则（ ）
A．B．C．D．
6．已知函数是上的奇函数，且，且当时，，则的值为（ ）
A．B．C．D．
7．已知是定义在R上的奇函数，若为偶函数且，则（ ）
A．B．C．D．6
【巩固练习】
一、单选题
1．下列函数中，在其定义域内既是奇函数又是减函数的是（ ）
A．B．C．D．
2．已知函数，不等式的解集为（ ）
A．B．
C．D．
3．已知函数在区间的最大值是M，最小值是m，则的值等于( )
A．0B．10C．D．
4．已知函数的图象关于原点对称，且，当时，，则（ ）
A．-11B．-8C．D．
二、多选题
5．下面关于函数的性质，说法正确的是（ ）
A．的定义域为B．的值域为
C．在定义域上单调递减D．点是图象的对称中心
6．已知定义在R上的偶函数的图像是连续的，，在区间上是增函数，则下列结论正确的是（ ）
A．的一个周期为6B．在区间上单调递减
C．的图像关于直线对称D．在区间上共有100个零点
7．（2022·重庆巴蜀中学高三阶段练习）已知函数对任意都有，若函数的图象关于对称，且对任意的，且，都有，若，则下列结论正确的是（ ）
A．是偶函数B．
C．的图象关于点对称D．
8．已知函数，，，则（ ）
A．的图象关于对称 B．的图象没有对称中心
C．对任意的，的最大值与最小值之和为
D．若，则实数的取值范围是
三、填空题
9．已知函数是偶函数，则__________．
10．已知函数在上的最小值为1，则的值为________.
11．（2022·广东佛山·三模）已知函数的图象关于原点对称，若，则的取值范围为________．
12．若函数f（x）同时满足：（1）对于定义域上的任意x，恒有；（2）对于定义域上的任意，当，恒有，则称函数f（x）为“理想函数”，下列①，②，③，④四个函数中，能被称为“理想函数”的有___________.（填出函数序号）奇偶性
定义
图象特点
偶函数
如果函数的定义域内任意一个
都有，那么函数是偶函数
关于对称
奇函数
如果函数的定义域内任意一个
都有，那么函数是奇函数
关于原点对称