广东省广州市花都区2022-2023学年八年级上学期期末数学试卷

2022-2023学年广东省广州市花都区八年级第一学期期末数学试卷

一．选择题（共10小题，满分30分）

1. 若分式有意义，则的取值范围是（    ）

A.      B.  C.  D.

【答案】B

【解析】

【分析】分式有意义时，分母x-2≠0，由此求得x取值范围．

【详解】依题意得：x-2≠0，

解得x≠2．

故选B．

【点睛】本题考查了分式有意义的条件．分式有意义的条件是分母不等于零．

2. 若一个三角形的两边长分别为、，则它的第三边的长可能是（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据三角形的三边关系：任意两边之和大于第三边进行判断即可．

【详解】解：由三角形的三边关系可得：

＜第三边＜，

即： 3＜第三边＜9，

故选C．

【点睛】本题考查三角形的三边关系，任意两边之和大于第三边，任意两边之差小于第三边．

3. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD的是（ ）

A. ∠B=∠C B. AD=AE C. BD=CE D. BE=CD

【答案】D

【解析】

【分析】欲使△ABE≌△ACD，已知AB＝AC，可根据全等三角形判定定理AAS、SAS、ASA添加条件，逐一证明即可．

【详解】解：∵AB＝AC，∠A为公共角，

A、如添加∠B＝∠C，利用ASA即可证明△ABE≌△ACD，不符合题意；

B、如添AD＝AE，利用SAS即可证明△ABE≌△ACD，不符合题意；

C、如添BD＝CE，等量关系可得AD＝AE，利用SAS即可证明△ABE≌△ACD，不符合题意；

D、如添BE＝CD，因为SSA，不能证明△ABE≌△ACD，所以此选项不能作为添加的条件，符合题意．

故选：D．

【点睛】本题主要考查学生对全等三角形判定定理的理解和掌握，此类添加条件题，要求学生应熟练掌握全等三角形的判定定理．

4. 下列运算正确的是（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】利用合并同类项的法则，同底数幂的乘法的法则，幂的乘方与积的乘方的法则对各项进行运算即可．

【详解】解：A、，选项错误，故不符合题意；

B、，选项错误，故不符合题意；

C、，选项正确，故符合题意；

D、，选项错误，故不符合题意；

故选：C．

【点睛】本题主要考查合并同类项，幂的乘方与积的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握．

5. 下列因式分解变形正确的是（　　）

A.  B.

C.  D.

【答案】B

【解析】

【分析】根据提公因式分解因式可得出A错误；根据完全平方公式可得B正确；根据平方差公式可得C错误；根据十字相乘法可判断D错误．

【详解】A、，故此选项错误；

B、，故此选项正确；

C、，故此选项错误；

D、，故此选项错误．

故选：B

【点睛】本题主要考查了因式分解，要灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要提取公因式，再考虑运用公式法分解．

6. 将分式中的、的值同时扩大倍，则分式的值（　　）

A. 扩大倍 B. 缩小到原来的 C. 保持不变 D. 无法确定

【答案】C

【解析】

【分析】利用分式的基本性质，进行计算即可解答．

【详解】解：将分式中的、的值同时扩大倍为，

即分式的值保持不变，

故选：C．

【点睛】本题考查了分式的基本性质，熟练掌握分式的基本性质是解题的关键．

7. 已知x2+mx+25是完全平方式，则m的值为（　　）

A. 10 B. ±10 C. 20 D. ±20

【答案】B

【解析】

【分析】根据完全平方式的特点求解：a2±2ab+b2.

【详解】∵x2+mx+25是完全平方式，

∴m=±10，

故选：B．

【点睛】本题考查了完全平方公式:a2±2ab+b2,其特点是首平方，尾平方，首尾积的两倍在中央，这里首末两项是x和1的平方，那么中间项为加上或减去x和1的乘积的2倍．

8. 如图，在中，，，，，则的长为（    ）

A. 1.5 B. 2 C. 3 D. 4

【答案】B

【解析】

【分析】根据直角三角形两锐角互余求出，然后根据角所对的直角边等于斜边的一半求出，再求出，然后求出，从而得到，根据等角对等边可得，从而得解．

【详解】解：，，

，

，

，，

，

，

，

．

故选：B．

【点睛】本题考查了直角三角形角所对的直角边等于斜边的一半的性质，直角三角形两锐角互余的性质，等角对等边的性质，解题的关键是掌握相应的性质定理．

9. 如图，中，，根据尺规作图的痕迹判断以下结论错误的是（    ）

A.  B.  C.  D.

【答案】D

【解析】

【分析】由尺规作图可知AD是∠CAB角平分线，DE⊥AC，由此逐一分析即可求解．

【详解】解：由尺规作图可知，AD是∠CAB角平分线，DE⊥AC，

在△AED和△ABD中：

∵，∴△AED≌△ABD(AAS)，

∴DB=DE，AB=AE，选项A、B都正确，

又在Rt△EDC中，∠EDC=90°-∠C，

在Rt△ABC中，∠BAC=90°-∠C，

∴∠EDC=∠BAC，选项C正确，

选项D，题目中缺少条件证明，故选项D错误．

故选：D.

【点睛】本题考查了尺规作图角平分线的作法，熟练掌握常见图形的尺规作图是解决这类题的关键．

10. 如图，BN为∠MBC的平分线，P为BN上一点，且PD⊥BC于点D，∠APC+∠ABC＝180°，给出下列结论：①∠MAP＝∠BCP；②PA＝PC；③AB+BC＝2BD；④四边形BAPC的面积是△PBD面积的2倍，其中结论正确的个数有（　　）

A. 4个 B. 3个 C. 2个 D. 1个

【答案】A

【解析】

【分析】过点P作PK⊥AB，垂足为点K．证明Rt△BPK≌Rt△BPD，△PAK≌△PCD，利用全等三角形的性质即可解决问题．

【详解】解：过点P作PK⊥AB，垂足为点K．

∵PK⊥AB，PD⊥BC，∠ABP＝∠CBP，

∴PK＝PD，

在Rt△BPK和Rt△BPD中，

，

∴Rt△BPK≌Rt△BPD（HL），

∴BK＝BD，

∵∠APC+∠ABC＝180°，且∠ABC+∠KPD＝180°，

∴∠KPD＝∠APC，

∴∠APK＝∠CPD，故①正确，

在△PAK和△PCD中，

，

∴△PAK≌△PCD（ASA），

∴AK＝CD，PA＝PC，故②正确，

∴BK﹣AB＝BC﹣BD，

∴BD﹣AB＝BC﹣BD，

∴AB+BC＝2BD，故③正确，

∵Rt△BPK≌Rt△BPD，△PAK≌△PCD（ASA），

∴S△BPK＝S△BPD，S△APK＝S△PDC，

∴S四边形ABCP＝S四边形KBDP＝2S△PBD．故④正确．

故选A．

【点睛】本题考查全等三角形的判定和性质，角平分线的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．

二．填空题（共6小题，满分18分）

11. 计算a2•（﹣6ab）的结果是 ___．

【答案】

【解析】

【分析】利用单项式乘以单项式的法则计算即可．

【详解】∵•（﹣6ab）=，

故答案为：．

【点睛】本题考查了单项式的乘法，熟练掌握单项式乘以单项式的法则是解题的关键．

12. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．

【答案】6##六

【解析】

【分析】根据多边形的内角和公式与外角和定理列出方程，求解即可得到答案．

【详解】解：设这个多边形的边数为，

根据题意得：，

解得：，

故答案为：6．

【点睛】本题考查了多边形内角和公式，多边形外角和定理，解题关键是掌握多边形内角和公式：以及多边形的外角和等于360．

13. 因式分解：______．

【答案】y（x+2）（x-2）

【解析】

【分析】先提取公因式y，再利用平方差公式分解因式即可

【详解】解：x2y﹣4y=y（x2﹣4）=y（x﹣2）（x+2）．

故答案为：y（x﹣2）（x+2）．

【点睛】题目主要考查提公因式法与公式法进行因式分解，熟练掌握因式分解的方法是解题关键．

14. 若 ，则___________．

【答案】15

【解析】

【分析】根据幂的乘方的逆运算得出 ，再由同底数幂乘法的逆运算求解即可．

【详解】解：∵ ，

∴，

故答案为：15．

【点睛】题目主要考查幂的乘方的逆运算及同底数幂的乘法的逆运算，求代数式的值，熟练掌握运算法则是解题关键．

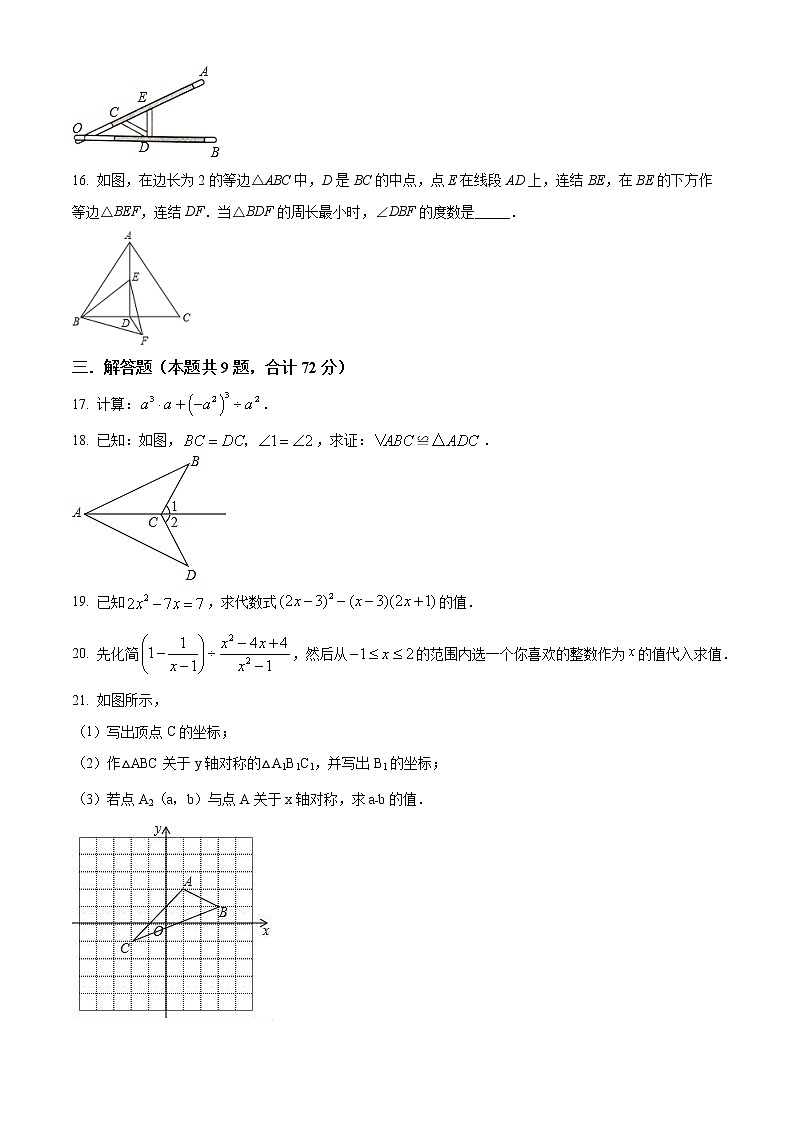
15. 借助如图所示的“三等分角仪”能三等分某些度数的角，这个“三等分角仪”由两根有槽的棒，组成，两根棒在点相连并可绕转动，点固定，，点，可在槽中滑动．若，则______

【答案】

【解析】

【分析】由等边对等角即可得出，．再结合三角形外角性质即可求出，从而可求出的大小．

【详解】解：∵，

∴，．

∵，，

∴，

∴，

∴．

故答案为：．

【点睛】本题考查等腰三角形的性质，三角形外角的性质．利用数形结合的思想是解题关键．

16. 如图，在边长为2的等边△ABC中，D是BC的中点，点E在线段AD上，连结BE，在BE的下方作等边△BEF，连结DF．当△BDF的周长最小时，∠DBF的度数是_____．

【答案】30°

【解析】

【分析】连接CF，由条件可以得出∠ABE＝∠CBF，再根据等边三角形的性质就可以证明△BAE≌△BCF，从而可以得出∠BCF＝∠BAD＝30°，作点D关于CF的对称点G，连接CG，DG，则FD＝FG，依据当B，F，G在同一直线上时，DF+BF的最小值等于线段BG长，可得△BDF的周长最小，再根据等边三角形的性质即可得到∠DBF的度数．

【详解】如图，连接CF，

∵△ABC、△BEF都是等边三角形，

∴AB＝BC＝AC，BE＝EF＝BF，∠BAC＝∠ABC＝∠ACB＝∠EBF＝∠BEF＝∠BFE＝60°，

∴∠ABC﹣∠EBD＝∠EBF﹣∠EBD，

∴∠ABE＝∠CBF，

在△BAE和△BCF中，

，

∴△BAE≌△BCF（SAS），

∴∠BCF＝∠BAD＝30°，

如图，作点D关于CF的对称点G，连接CG，DG，则FD＝FG，

∴当B，F，G在同一直线上时，DF+BF的最小值等于线段BG长，此时△BDF的周长最小，

由轴对称的性质，可得∠DCG＝2∠BCF＝60°，CD＝CG，

∴△DCG是等边三角形，

∴DG＝DC＝DB，

∴∠DBG＝∠DGB＝∠CDG＝30°，

故答案为30°．

【点睛】本题考查了全等三角形的判定与性质，等边三角形的性质的运用．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．

三．解答题（本题共9题，合计72分）

17. 计算：．

【答案】

【解析】

【分析】根据同底数幂的乘法和除法的运算法则，幂的乘方的运算法则解答即可．

【详解】解：原式

．

【点睛】本题主要考查了同底数幂的乘法和除法的运算法则，幂的乘方的运算法则，熟记幂的运算法则是解答本题的关键．

18. 已知：如图，，求证：≌．

【答案】见解析

【解析】

【分析】先证明，再结合，，即可得到结论．

【详解】．证明：，

，

，

≌．

【点睛】本题考查的是全等三角形的判定，掌握“利用证明两个三角形全等”是解本题的关键．

19. 已知，求代数式的值．

【答案】19

【解析】

【分析】先通过整式的运算法则将代数式化简成，再整体代入求值．

【详解】解：原式

∵，

∴，

∴原式．

【点睛】本题考查整式的化简求值，解题的关键是掌握整体代入的思想求值．

20. 先化简，然后从的范围内选一个你喜欢的整数作为的值代入求值．

【答案】，

【解析】

【分析】先计算括号内的，再计算除法，然后根据分式有意义的条件，可得x取0，再代入化简后的结果，即可求解．

【详解】解：

根据题意得：且，

解得，1，2，

∵且x为整数，

∴x取0，

当时，原式

【点睛】本题主要考查了分式的化简求值，熟练掌握分式的混合运算法则是解题的关键．

21. 如图所示，

（1）写出顶点C的坐标；

（2）作△ABC关于y轴对称的△A1B1C1，并写出B1的坐标；

（3）若点A2（a，b）与点A关于x轴对称，求a﹣b的值．

【答案】（1）C（﹣2，﹣1）；（2）△ABC关于y轴对称的△A1B1C1见解析；B1（﹣3，1）；（3）a﹣b=3．

【解析】

【详解】试题分析：（1）观察图形，直接写出点C的坐标即可；（2）在平面直角坐标系中，分别找出点A、B、C关于y轴对称点A1、B1、C1，顺次连接即可；（3）根据点A的坐标求得点A2的坐标，即可得a、b的值，从而求得a-b的值.

试题解析：

（1）C（-2，-1）

（2）如图，B1（-3，1）

（3）∵A（1，2）与A2（a，b）关于x轴对称，可得：a=1，b=-2 ，

∴a-b=3．

22. 如图，中，，点是上一点，，连接，是的角平分线，交于点，交于点，连接．

（1）若，求的度数；

（2）求证：．

【答案】（1）   

（2）见解析

【解析】

【分析】（1）根据角平分线定义和三角形内角和定理即可解决问题；

（2）证明，即可解决问题．

【小问1详解】

解：在中，，

，

，

，是的角平分线，

，，

，

，

；

【小问2详解】

证明：在和中，

，

，

．

【点睛】本题考查全等三角形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形．

23. 如图，在等边中，是边上一点（不含端点，），是的外角的平分线上一点，且．

（1）尺规作图：在直线的下方，过点作，作的延长线，与相交于点．

（2）求证：是等边；

（3）求证：．

【答案】（1）见解析    （2）见解析   

（3）见解析

【解析】

【分析】（1）以为圆心，以任意长为半径画弧，交、两边为和，以为圆心，以为半径画弧，交前弧于，作射线，交的延长线于，则；

（2）证明三个角都是，可得结论；

（3）作辅助线，构建三角形全等，证明（SAS），得，，证明，根据三角形外角的性质可得结论．

小问1详解】

如图所示：

【小问2详解】

证明：是等边三角形，

，

，

平分，

，

，

，

是等边；

小问3详解】

证明：连接，

和是等边三角形，

，

在和中，

，

（SAS），

，，

，

，

，

，

，

，

，

．

【点睛】本题综合考查了等边三角形的性质和判定，作一个角等于已知角的基本作图，全等三角形的判定与性质，三角形的外角性质等知识，熟练掌握等边三角形的性质，通过作辅助线构造三角形全等是解本题的关键．

24. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．

（1）如图1所示的大正方形，是由两个正方形和两个形状大小完全相同的长方形拼成的．用两种不同的方法计算图中阴影部分的面积，可以得到的数学等式是 　 　；

（2）如图2所示的大正方形，是由四个三边长分别为a、b、c的全等的直角三角形（a、b为直角边）和一个正方形拼成，试通过两种不同的方法计算中间正方形的面积，并探究a、b、c之间满足怎样的等量关系；

（3）利用（1）（2）的结论，如果直角三角形两直角边满足a+b＝17，ab＝60，求斜边c的值．

【答案】（1）（a+b）2=2ab+a2+b2；（2）a2+b2= c2，理由见详解；（3）13

【解析】

【分析】（1）用两种方法表示大正方形的面积，即可得到答案；

（2）用两种方法表示中间的正方形的面积，即可得到答案；

（3）利用（a+b）2=2ab+a2+b2和a2+b2= c2，代入求值，即可．

【详解】解：（1）由图形可知：∵大正方形的面积=2ab+a2+b2，大正方形面积=（a+b）2，

∴（a+b）2=2ab+a2+b2，

故答案是：（a+b）2=2ab+a2+b2；

（2）∵中间正方形的面积=c2，中间正方形的面积=（a+b）2-4×ab= a2+b2，

∴a2+b2= c2；

（3）由（1）可知：（a+b）2=2ab+a2+b2，

∴a2+b2=（a+b）2-2ab=172-2×60=169，

又∵a2+b2= c2，

∴c2=169，即c=13（负值舍去），

【点睛】本题主要考查完全平方公式勾股定理证明，结合图形，会用代数式表示同一个图形的面积是解题的关键．

25. 如图，已知等腰直角△ABC中，，以为边在点A的另一侧作等边，点F，G分别在线段，上，，且，与相交于点H，延长交于E．

（1）求证：是等边三角形；

（2）试判断线段和的数量关系，并说明理由．

（3）若点M是边上的动点，AB＝a，，，求周长的最小值（结果用含a，b，c的整式表示）．

【答案】（1）见解析    （2），理由见解析   

（3）

【解析】

【分析】（1）由推出推出只要证明即可解决问题；

（2）如图2中，如图2中，连接．由可得推出，中，即可推出由此即可解决问题；

（3）如图3中，延长交的延长线于，连接．由，推出，推出，推出的最小值为推出的周长最小值，由此即可解决问题；

【小问1详解】

如图1中，

是等边三角形，   

是等边三角形．

【小问2详解】

如图2中，如图2中，连接．

是等边三角形，   

在中，   

【小问3详解】

如图3中，延长交的延长线于，连接．

的最小值为

【点睛】本题考查三角形综合题、等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用对称解决最短问题，属于中考压轴题．