
2023高考数学复习专项训练《空间直线、平面的垂直》
展开
2023高考数学复习专项训练《空间直线、平面的垂直》
一 、单选题(本大题共8小题,共40分)
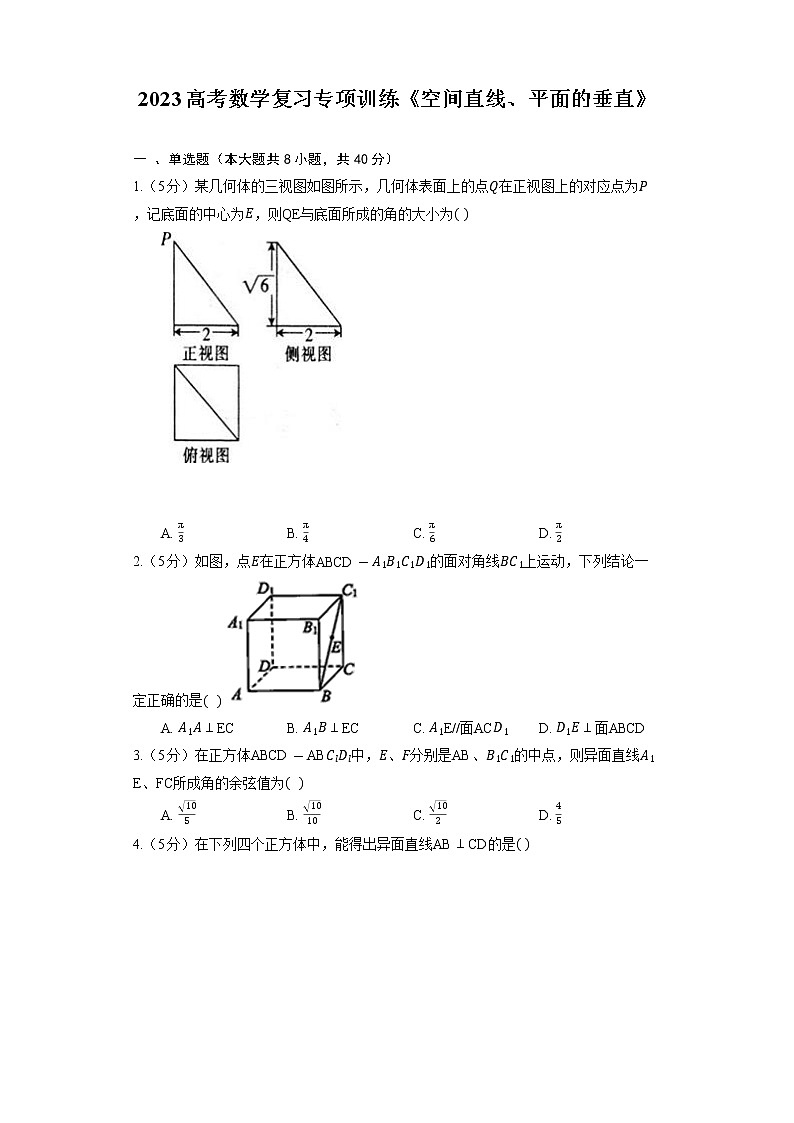
1.(5分)某几何体的三视图如图所示,几何体表面上的点Q在正视图上的对应点为P,记底面的中心为E,则QE与底面所成的角的大小为( )
A. π3 B. π4 C. π6 D. π2
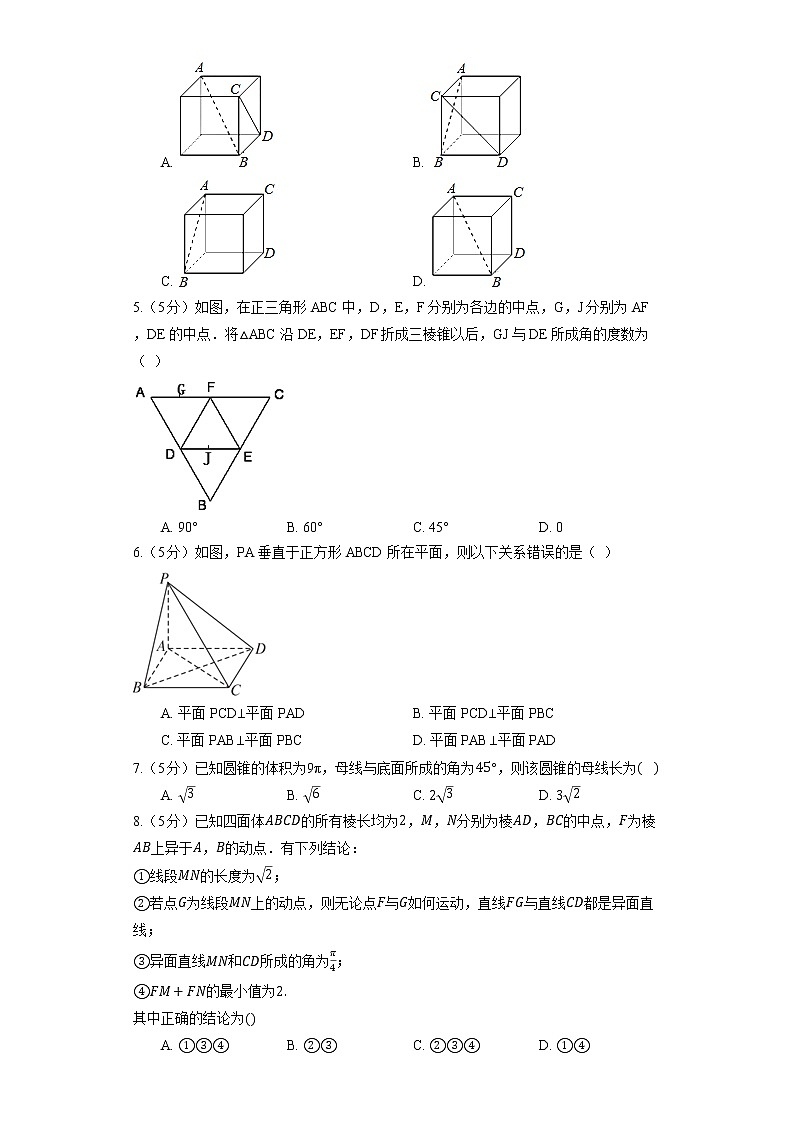
2.(5分)如图,点E在正方体ABCD-A1B1C1D1的面对角线BC1上运动,下列结论一定正确的是( )
A. A1A⊥EC B. A1B⊥EC C. A1E//面ACD1 D. D1E⊥面ABCD
3.(5分)在正方体ABCD-ABClDl中,E、F分别是AB、B1C1的中点,则异面直线A1E、FC所成角的余弦值为( )
A. 105 B. 1010 C. 102 D. 45
4.(5分)在下列四个正方体中,能得出异面直线AB⊥CD的是( )
A. B.
C. D.
5.(5分)如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )
A. 90° B. 60° C. 45° D. 0
6.(5分)如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
A. 平面PCD⊥平面PAD B. 平面PCD⊥平面PBC
C. 平面PAB⊥平面PBC D. 平面PAB⊥平面PAD
7.(5分)已知圆锥的体积为9π,母线与底面所成的角为45°,则该圆锥的母线长为( )
A. 3 B. 6 C. 23 D. 32
8.(5分)已知四面体ABCD的所有棱长均为2,M,N分别为棱AD,BC的中点,F为棱AB上异于A,B的动点.有下列结论:
①线段MN的长度为2;
②若点G为线段MN上的动点,则无论点F与G如何运动,直线FG与直线CD都是异面直线;
③异面直线MN和CD所成的角为π4;
④FM+FN的最小值为2.
其中正确的结论为()
A. ①③④ B. ②③ C. ②③④ D. ①④
二 、多选题(本大题共5小题,共25分)
9.(5分)如图,在棱长为2的正方体ABCD-A1B1C1D1中,P,Q分别为棱BC,CC1的中点,则以下四个结论中正确的是( )
A. B1Q⊥AD1 B. PQ⊥平面A1DCB1
C. AD1//平面DPQ D. 点Q到平面AB1P的距离为62
10.(5分)如图,在正方体ABCD-A1B1C1D1中,下面结论正确的是( )
A. BD//平面CB1D1 B. AC1⊥BD
C. 平面ACC1A1⊥CB1D1 D. 异面直线AD与CB1所成的角为60°
11.(5分)已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则下列结论正确的是( )
A. 棱AB与PD所在直线垂直; B. 平面PBC与平面ABCD垂直;
C. ΔPCD的面积大于ΔPAB的面积; D. 直线AE与直线BF是异面直线.
12.(5分)如图,已知正方体ABCD-A1B1C1D1中,E,F,M,N分别是CD,A1B1,DD1,BC的中点,则下列说法正确的有( )
A. E,F,M,N四点共面
B. BD与EF所成的角为π3
C. 在线段BD上存在点P,使PC1⊥平面EFM
D. 在线段A1B上任取点Q,三棱锥Q-EFM的体积不变
13.(5分)如图,线段AB为圆O的直径,点E,F在圆O上,EF // AB,矩形ABCD所在平面和圆O所在平面垂直,且AB=2,EF=AD=1,则下述正确的是( )
A. OF // 平面BCE
B. BF⊥平面ADF
C. 点A到平面CDFE的距离为217
D. 三棱锥C-BEF外接球的体积为5π
三 、填空题(本大题共5小题,共25分)
14.(5分)已知圆O和圆M是球O的大圆和小圆,其公共弦长为球O半径的3倍,且圆O和圆M所在平面所成的二面角是30°,OM=1,则圆O的半径为______.
15.(5分)a,b为异面直线,且a,b所成角为40°,直线c与a,b均异面,且所成角均为70°,则这样的c共有____________条.
16.(5分)已知圆柱底面半径为r,O是上底面圆心,A、B是下底面圆周上两个不同的点,母线BC长为3.如图,若直线OA与BC所成角的大小为π6,则r=______ .
17.(5分)如图梯形ABCD中,AD//BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:
①DF⊥BC,
②BD⊥FC
③平面DBF⊥平面BFC,
④平面DCF⊥平面BFC.
在翻折过程中,可能成立的结论是______.(填写结论序号)
18.(5分)已知两条异面直线a与b所成角为30,P是空间一点,若过点P与a和b所成角都是θ的直线有4条,则θ的范围是 ______.
四 、解答题(本大题共5小题,共60分)
19.(12分)如图,在四棱锥P-ABCD中,底面ABCD为矩形,点E在棱AD上,且DE=2AE,PE⊥底面ABCD,BC=23,AB=PE=2.
(1)证明:AC⊥PB;
(2)求平面PBE与平面PCD所成锐二面角的余弦值.
20.(12分)如图,在三棱锥中,,,为的中点,,=,求证:平面⊥平面.
21.(12分)如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC//平面EAD;
(Ⅲ)求二面角A-FC-B的余弦值.
22.(12分)如图,在四棱锥P-ABCD中,底面四边形ABCD为直角梯形,AB//CD,AB⊥BC,AB=2CD=2BC,O为BD的中点,BD=4,PB=PC=PD=5.
(1)证明:OP⊥平面ABCD;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
23.(12分)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD,AD//BC,∠ADC=90°,BC=12AD=1,CD=3,Q,M分别为AD,PC的中点.
(1)求证:MB=MQ;
(2)直线PB与平面ABCD所成角的大小为45°,求点P到平面MQB的距离.
答案和解析
1.【答案】A;
【解析】
此题主要考查的是三视图和线面所成角,是基础题.
解:由题知,其图如下,
则QA⊥面ABCD,QA=6,AD=AB=2,
所以AE=2,
所以tan∠QAE=QAAE=62=3,⇒∠QAE=π3.
则QE与底面所成的角的大小为∠QAE=π3.
故选A.
2.【答案】C;
【解析】解:由A1A//CC1,CC1不垂直于EC,A1A⊥EC不正确,故A错误;
由A1B//D1C,当E为BC1的中点时,A1B与EC成60°的角,故B错误;
由A1C1//AC,A1B//D1C,可得平面A1BC//平面ACD1,
而A1E⊂平面A1BC,可得A1E//面ACD1,故C正确;
当E与B重合时,D1E不垂直于面ABCD,故D错误.
故选:C.
由线线垂直的性质可判断A;由异面直线所成角可判断B;由面面平行的判定定理和性质,可判断C;由线面的位置关系可判断D.
该题考查空间线线,线面的位置关系,主要是平行和垂直的判定和性质,考查推理能力,属于基础题.
3.【答案】D;
【解析】解:以A为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设正方体ABCD-ABClDl中棱长为2.
则A1(2,0,2),E(2,1,0),F(1,2,2),C(0,2,0),
A1→E=(0,1,-2),FC→=(-1,0,-2),
设异面直线A1E、FC所成角为θ,
则cosθ=|A1→E.FC→||A1→E|.|FC→|=45.5=45.
故异面直线A1E、FC所成角的余弦值为45.
故选:D.
以A为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出异面直线A1E、FC所成角的余弦值.
该题考查异面直线所成角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是基础题.
4.【答案】A;
【解析】解:对于A,作出过AB的对角面ABE,如图,
可得直线CD与这个对角面ABE垂直,
根据线面垂直的性质,AB⊥CD成立,故A正确;
对于B,作出过AB的等边三角形截面ABE,如图,
将CD平移至内侧面,
可得CD与AB所成角等于60°,故B不成立;
对于C、D,将CD平移至经过B点的侧棱处,
可得AB、CD所成角都是锐角,
故C和D均不成立.
故选:A.
对于A,作出过AB的对角面ABE,可得直线CD与这个对角面ABE垂直,从而AB⊥CD成立;对于B,作出过AB的等边三角形截面ABE,得CD与AB所成角等于60°;对于C、D,将CD平移至经过B点的侧棱处,得AB、CD所成角都是锐角.
此题主要考查四个正方体中,能得出异面直线AB⊥CD的正方体的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
5.【答案】A;
【解析】解:连接DG、GE,
根据题意可知三棱锥为正四面体
点G为AF的中点,则DG=GE
而点J为DE的中点,则GJ⊥DE
∴GJ与DE所成角的度数为90°
故选A.
6.【答案】B;
【解析】证明:由于CD⊥AD,由PA垂直于正方形ABCD所在平面,所以CD⊥PA,易证CD⊥平面PAD,则平面PCD⊥平面PAD;
由于BC⊥AB,由PA垂直于正方形ABCD所在平面,所以BC⊥PA,易证BC⊥平面PAB,则平面PAB⊥平面PBC;
又AD∥BC,故AD⊥平面PAB,则平面PAD⊥平面PAB.
故选:B.
7.【答案】D;
【解析】
此题主要考查圆锥的体积以及直线与平面所成角的应用,考查空间想象能力以及计算能力.
设出圆锥底面半径,利用已知条件求出底面半径,然后求解圆锥的母线长即可.
解:圆锥的体积为9π,母线与底面所成的角为45°,可知圆锥的母线与母线在底面上的射影即底面半径的夹角为45°,
所以圆锥的高与底面半径相等,设为r,所以13.π.r2.r=9π,所以r=3,
该圆锥的母线长为32.
故选:D.
8.【答案】A;
【解析】解:连接AN,DN,四面体ABCD的所有棱长均为2,则AN=DN=3,且MN⊥AD,
所以MN=3-1=2,故①不正确;
取AB的中点F,CD的中点E,FM//BD且FM=12BD,NE//BD,NE=12BD,
所以FM//NE,FM=NE,
所以四边形FNEM是平行四边形,MN与EF相交于点G,所以此时FG与CD相交,不是异面直线,故②不正确;
取BD的中点,连接HN,HM,
M,N分别为棱AD,BC的中点,所以MH=12AB=1,HN=12CD=1,NH//CD,
所以∠HNM为异面直线MN和CD所成的角,又MH2+NH2=MN2,
故△HMN为等腰直角三角形,所以异面直线MN和CD所成的角为π4,故③正确;
将面ABD、面ABC展开为一个平面,如下图:
当M,F,N共线时,MF+FN最小为MN=2,故④正确.
故选:A.
①连接AN,DN,易知△AND为等腰三角形,即MN⊥AD,即可求MN的长;
②构造平行四边形FNEM,探讨它们的关系可判断;
③取BD的中点,连接HNd,HM,可证△HMN为等腰直角三角形,从而可得结论;
④将面ABD、面ABC展开为一个平面,判断NF+FN最小的情况即可.
此题主要考查了正四面体的性质、异面直线所成的角,外接球的体积及将展面开求线段的最小值,属于中档题.
9.【答案】BCD;
【解析】解:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系如图所示,
则D(0,0,0),A(2,0,0),D1(0,0,2),P(1,2,0),
Q(0,2,1),A1(2,0,2),B1(2,2,2),C(0,2,0),
对于选项A,A→D1=(-2,0,2),B1→Q=(-2,0,-1),
则有A→D1.B1→Q=4-2=2≠0,∴B1Q与AD1不垂直,故A错误;
对于选项B,PQ→=(-1,0,1),D→A1=(2,0,2),DC→=(0,2,0),
∵PQ→.D→A1=0,PQ→.DC→=0,且DA1∩DC=D,∴PQ⊥平面A1DCB1,故B正确;
对于选项C,∵PQ//BC1,AD1//BC1,∴AD1//PQ,
而AD1⊄平面DPQ,PQ⊂平面DPQ,∴AD1//平面DPQ,故C正确;
对于选项D,∵AP→=(-1,2,0),B1→P=(-1,0,-2),
设平面AB1P的法向量为n→=(x,y,z),
则有n→.AP→=-x+2y=0n→.B1P=-x-2z=0,令y=1,则x=2,z=-1,得n→=(2,1,-1),
故Q到平面AB1P的距离为|PQ→.n→||n→|=|-2-1|6=62,故D正确.
故选:BCD.
建立空间直角坐标系,求出所需的向量,利用直线的方向向量是垂直判断选项A,利用直线与平面垂直的判定判断选项B,利用线面平行的判定判断选项C,利用点到面的距离公式判断选项D.
此题主要考查了空间向量在立体几何中的应用,涉及了利用直线的方向向量判断两条直线位置关系、线面平行及垂直的判定、点到面距离公式的应用,属于中档题.
10.【答案】ABC;
【解析】
此题主要考查异面直线所成的角、线面平行的判定定理、线面垂直的判定定理、面面垂直的判定定理,属中档题.
按照定理逐项判断即可得到最后结果.
解:因为BD//B1D1,B1D1⊂平面CB1D1,BD⊄平面CB1D1,
所以BD//平面CB1D1,故A正确;
连接AC,则AC⊥BD,
又因为CC1⊥BD,CC1∩AC=C,CC1,AC⊂平面ACC1,
∴BD⊥平面ACC1,
∵AC1⊂平面ACC1,
∴AC1⊥BD,故B正确;
同理可得AC1⊥B1C,AC1⊥B1D1,
又因为B1C∩B1D1=B1,B1C,B1D1∈平面CB1D1,
∴AC1⊥平面CB1D1,
∵AC1⊂平面ACC1A1,
∴平面ACC1A1⊥CB1D1,故C正确;
因为AD//BC,
所以∠BCB1为异面直线AD与CB1所成的角,
故异面直线AD与CB1所成的角为45°,故D错误.
故选ABC.
11.【答案】AC;
【解析】
此题主要考查空间直线与直线、平面与平面位置关系的判断,属于中档题.利用线面垂直的判断及性质、面面垂直的性质逐一判断.
解:如图:
因为PA⊥底面ABCD,AB在平面ABCD内,
所以PA⊥AB,
又底面ABCD为矩形,
则AB⊥AD,
AD、PA在平面PAD内,且相交于点A,
则AB⊥平面PAD,PD在平面PAD内,
所以AB⊥PD,
故A正确;
平面PBC与平面ABCD不垂直,
若平面PBC与平面ABCD垂直,
因为AB⊥BC,平面PBC与平面ABCD的交线为BC,
则AB⊥平面PBC,
所以AB与PB垂直,
由题意知,AB与PB不垂直,
故B错误;
因为AB⊥PD,AB//CD,
所以CD⊥PD,又AB⊥PA,
所以SΔ=12AB×PA,SΔ=12PD×CD,
又AB=CD且PA
故C正确;
点E、F分别是棱PC、PD的中点,
则EF//CD,又CD//AB,
所以EF//AB,
则AB与EF共面,
所以AE与BF共面,
故D错误.
以上结论正确的是AC.
故选AC.
12.【答案】ABD;
【解析】解:以点D为坐标原点,建立如图所示的空间直角坐标系D-xyz,
令AB=2,则E(0,1,0),F(2,1,2),M(0,0,1),N(1,2,0),
∴EF→=(2,0,2),FM→=(-2,-1,-1),MN→=(1,2,-1),
取向量m→=(1,-1,-1),注意到m→⋅EF→=m→⋅FM→=m→⋅MN→=0
即平面EFM和平面FMN的法向量相同,据此可得E,F,M,N四点共面,选项A正确;
由于B(2,2,0),D(0,0,0),E(0,1,0),F(2,1,2),
故BD→=(-2,-2,0),EF→=(2,0,2).
由于BD→⋅EF→=-4,|BD→|=|EF→|=8,
故设BD与EF所成的角为θ,则|cosθ|=|BD→⋅EF→||BD→|×|EF→|=48=12,∴θ=π3,
选项B正确;
对应选项C,设P(m,m,0)(0⩽m⩽2),G(0,2,2),
∴P→C1=(-m,2-m,2),
由于平面EFM的法向量m→=(1,-1,-1),
故P→C1⋅m→=-m+m-2-2≠0,据此可得选项C错误;
由于A1(2,0,2),B(2,2,0),E(0,1,0),M(0,0,1),
故A1→B=(0,2,-2),EM→=(0,-1,1),∴A1→B//øverrightarrowEM,
从而有直线A1B//平面EFM,点Q到平面EFM的距离为定值,选项D正确.
故选:ABD.
建立空间直角坐标系,利用空间直角坐标系的相关结论考查所给的选项是否正确即可.
此题主要考查空间中的四点共面问题,异面直线所成的角的计算,线面垂直的判定,锥体体积的计算,空间向量的应用等知识,属于中等题.
13.【答案】ABC;
【解析】
该题考查简单多面体(棱柱、棱锥、棱台)及其结构特征,棱柱、棱锥、棱台的侧面积、表面积和体积,球的表面积和体积,
线面平行的判定,线面垂直的判定,考查逻辑推理能力和空间想象能力,属于中档题.
由线面平行与垂直的判定定理,等体积转化,球的体积公式对选项逐一判定可得结论.
解:
对于A,连接OF,∵EF // AB,AB=2,EF=1,∴EF // =OB,
则四边形OBEF是平行四边形,∴OF//BE,∵BE⊂平面BCE,
OF⊄平面BCE,∴OF//平面BCE,故A正确;
对于B,由题意,平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
AD⊥AB,AD⊂平面ABCD,∴AD⊥平面ABEF,BF⊂平面ABEF,∴AD⊥BF,
又∵AB是圆O的直径,∴BF⊥AF,AF∩AD=A,AF、AD⊂平面ADF,
∴BF⊥平面ADF,故B正确;
对于C,设点A到平面CDFE的距离为h,即点A到平面CDF的距离为h,
∵由A可得,四边形ABEF是等腰梯形,AB=2,BE=AF=EF=1,取AO的中点G,
过点G作GM//AD,与CD交于点M,连接GF,MF,则GF⊥AO,
又平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,GF⊂平面ABEF,
∴GF⊥平面ABCD,且易得GF=3 2,
∵AD⊥AO,∴MG⊥AO,MG∩GF=G,MG、GF⊂平面MGF,
∴AO⊥平面MGF,MF⊂平面MGF,∴AO⊥MF,则CD⊥MF,
且MF=MG2+GF2=1+3 4=7 2,
∵VA-CDF=VF-ACD,∴1 3×1 2CD.MF.h=1 3×1 2CD.AD.GF,
∴MF.h=AD.GF,解得h=1×3 2 7 2=21 7,故C正确;
对于D,∵B,E,F在圆O上,则圆O是ΔBEF的外接圆,
则ΔBEF的外接圆为r=1,
则三棱锥C-BEF外接球的半径为R=(BC 2 )2+r2=1 4+1=5 2,
∴三棱锥C-BEF外接球的体积为4 3 π×(5 2 )3=55 6 π,故D错误.
故选ABC.
14.【答案】4;
【解析】解:设两圆的公共弦长为AB,C为AB的中点,连结MC、OC,
则OC⊥AB,MC⊥AB,
则∠MCO就是圆O与圆M所在的平面所成的二面角的平面角,即∠MCO=30°
在RtΔMOC中,∵OM=1,∴OC=OMsin30∘=2,
在RtΔAOC中,OA2=OC2+AC2,即R2=4+(32R)2,
解得R=4,
故答案为:4.
设C是两圆的公共弦AB的中点,连结MC、OC,则OC⊥AB,MC⊥AB,可得∠MCO是题中二面角的平面角,得∠MCO=30°.在RtΔMOC中算出OC=2,再在RtΔAOC中根据勾股定理列式求得R值.
该题考查空间中线线、线面、面面间的位置关系、球等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.
15.【答案】3;
【解析】解:如图所示:先将异面直线a,b平移到点P,
BD∥a,CE∥,b,
则由题意可得∠BPE=40°、∠EPD=140°,
而∠BPE的角平分线与a和b的所成角为20°,
∠DPE的角平分线与a和b的所成角为70°,
故直线c可以是∠DPE的角平分线.
∵70°>20°,故与a、b所成的角相等且等于70°
有且只有3条,
另外2条直线c满足直线c在面EPD的射影为∠BPE的角平分线,
即图中直线c、d,
故答案为 3.
16.【答案】3;
【解析】解:如图,过A作与BC平行的母线AD,连接OD,
则∠OAD为直线OA与BC所成的角,
∴∠OAD=π6.
在直角三角形ODA中,tanπ6=rl=r3=33,
解得;r=3,
故答案为:3
过A作与BC平行的母线AD,由异面直线所成角的概念得到∠OAD=π6.在直角三角形ODA中,直接由tanπ6=rl得到答案.
此题主要考查了异面直线所成的角,考查了直角三角形的解法,是基础题.
17.【答案】②③;
【解析】
该题考查命题的真假判断,考查学生分析解决问题的能力,属于中档题.
①:因为BC//AD,AD与DF相交不垂直,所以BC与DF不垂直;
②:设点D的在平面BCF上的射影为点P,当BP⊥CF时就有BD⊥FC,而AD:BC:AB=2:3:4可使条件满足;
③:当点P落在BF上时,DP⊂平面BDF,从而平面BDF⊥平面BCF.
④:点D的射影不可能在FC上.
解:①:因为BC//AD,AD与DF相交不垂直,所以BC与DF不垂直,则①不成立;
②:设点D的在平面BCF上的射影为点P,当BP⊥CF时就有BD⊥FC,而AD:BC:AB=2:3:4可使条件满足,所以②正确;
③:当点P落在BF上时,DP⊂平面BDF,从而平面BDF⊥平面BCF,所以③正确.
④:因为点D的射影不可能在FC上,所以平面DCF⊥平面BFC不成立.
故答案为:②③.
18.【答案】75°<θ<90°;
【解析】解:过点O作a1//a,b1//b,
则相交直线a1,b1确定一个平面α,且a1,b1所成的角为150°或30°,
设直线OA与a1,b1均成θ角,
作AB⊥平面α于点B,BC⊥a1于点C,BD⊥b1于点D,
记∠AOB=θ1,∠BOC=θ2(θ2=15°或75°),
则有cosθ=cosθ1⋅cosθ2,
因为0°⩽θ1⩽90°,
所以0⩽cosθ⩽cosθ2,
当θ2=15°时,由0⩽cosθ⩽cos15°,可得15°⩽θ⩽90°;
当θ2=75°时,由0⩽cosθ⩽cos75°,可得75°⩽θ⩽90°;
故当θ<15°时,直线l不存在;
当θ=15°时,直线l有且仅有1条;
当15°<θ<75°时,直线有且仅有2条;
当θ=75°时,直线l有且仅有3条;
当75°<θ<90°时,直线有且仅有4条;
当θ=90°时,直线l有且仅有1条.
综上所述,θ的范围是75°<θ<90°.
故答案为:75°<θ<90°.
过点O作a1//a,b1//b,则相交直线a1,b1确定一个平面α,且a1,b1所成的角为150°或30°,设直线OA与a1,b1均成θ角,作AB⊥平面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2,(θ2=15°或75°),利用cosθ=cosθ1⋅cosθ2,进行角之间的大小比较,从而得到答案.
此题主要考查了异面直线所成角的理解与应用,考查了逻辑推理能力与空间想象能力,属于中档题.
19.【答案】解:(1)证明:设BE交AC于点F,
因为PE⊥底面ABCD,AC⊂底面ABCD,所以PE⊥AC.
因为BC∥AD,所以AFCF=EFBF=AEBC=13,
所以CF=34AC=34AB2+BC2=3,BF=34BE=34AB2+AE2=3,
所以BF2+CF2=BC2,所以BE⊥AC,
又PE∩BE=E,PE,BE⊂平面PBE,所以AC⊥平面PBE,
又PB⊂平面PBE,所以AC⊥PB.
(2)解:过F作FG∥PE,则FG⊥平面ABCD,∴FG⊥BF,FG⊥FC,
以F为原点,以FB→,FC→,FG→的方向分别为x,y,z轴的正方向建立如图所示的空间直角坐标系,
则P(-33,0,2),C(0,3,0),D(-3,2,0),
所以PC→=(33,3,-2),DC→=(3,1,0),
设平面PCD的一个法向量为m→=(x,y,z),
则{m→·PC→=0m→·DC→=0,即{33x+3y-2z=03x+y=0,
取x=3,则y=-3,z=-4,所以m=(3,-3,-4).
又平面PBE的一个法向量为n→=(0,1,0).
设平面PBE与平面PCD所成锐二面角为θ,
则cosθ=|m→·n→||m→|·|n→|=328=3714,
∴平面PBE与平面PCD所成锐二面角的余弦值为3714.;
【解析】
(1)设BE交AC于点F,则PE⊥AC,推导出BE⊥AC,从而AC⊥平面PBE,由此能证明AC⊥PB.
(2)过F作FG//PE,则FG⊥平面ABCD,可得FG⊥BF,FG⊥FC,以F为原点,FB→,FC→,FG→的方向分别为x,y,z轴的正方向建立空间直角坐标系,利用向量法能求出平面PBE与平面PCD所成锐二面角的余弦值.
此题主要考查线面垂直的判定与性质、线面平行的性质、向量法求二面角的余弦值等基础知识,考查运算求解能力,是中档题.
20.【答案】略;
【解析】证明:在中,,,,则为直角三角形,所以.又由已知,且是的中点,可得,又,平面又面,平面平���.
21.【答案】(Ⅰ)证明:设AC与BD相交于点O,
连接FO.因为四边形ABCD为菱形,所以AC⊥BD,且O为AC中点.
又 FA=FC,所以 AC⊥FO.
因为 FO∩BD=O,
所以 AC⊥平面BDEF.
(Ⅱ)证明:因为四边形ABCD与BDEF均为菱形,
所以AD//BC,DE//BF,
所以 平面FBC//平面EAD.
又FC⊂平面FBC,所以FC//平面EAD.
(Ⅲ)解:因为四边形BDEF为菱形,且∠DBF=60°,
所以ΔDBF为等边三角形.
因为O为BD中点,所以FO⊥BD,故FO⊥平面ABCD.
由OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O-xyz.
设AB=2.因为四边形ABCD为菱形,∠DAB=60°,
则BD=2,所以OB=1,OA=OF=3.所以 O(0,0,0),A(3,0,0),B(0,1,0),C(-3,0,0),F(0,0,3).
所以 CF→=(3,0,3),CB→=(3,1,0).
设平面BFC的法向量为n→=(x,y,z),
则有3x+3z=03x+y=0,
取x=1,得n→=(1,-3,-1).
∵平面AFC的法向量为v→=(0,1,0).
由二面角A-FC-B是锐角,得|cos
所以二面角A-FC-B的余弦值为155.;
【解析】该题考查直线与平面垂直、直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,合理地进行等价转化,注意向量法的合理运用.
(Ⅰ)设AC与BD相交于点O,连接FO.因为四边形ABCD为菱形,所以AC⊥BD,且O为AC中点.由FA=FC,知AC⊥FO.由此能够证明AC⊥平面BDEF.
(Ⅱ)因为四边形ABCD与BDEF均为菱形,所以AD//BC,DE//BF,平面FBC//平面EAD.由此能够证明FC//平面EAD.
(Ⅲ)因为四边形BDEF为菱形,且∠DBF=60°,所以ΔDBF为等边三角形.因为O为BD中点,所以FO⊥BD,故FO⊥平面ABCD.由OA,OB,OF两两垂直,建立空间直角坐标系O-xyz.设AB=2.因为四边形ABCD为菱形,∠DAB=60°,则BD=2,所以 CF→=(3,0,3),CB→=(3,1,0).求得平面BFC的法向量为n→=(1,-3,-1),平面AFC的法向量为v→=(0,1,0).由此能求出二面角A-FC-B的余弦值.
22.【答案】(1)证明:如图,连接OC,
在Rt△BCD中,由BD=4,可得OC=2,
因为PB=PD=5,OB=OD=2,
所以OP⊥BD,OP=PB2-OB2=5-4=1,
因为OP=1,OC=2,PC=5,
则PC2=OP2+OC2,
故OP⊥OC,
因为OP⊥BD,BD∩OC=O,BD,OC⊂平面ABCD,
则OP⊥平面ABCD;
(2)解:由(1)可知,OC,OB,OP两两垂直,
以点O为坐标原点,建立空间直角坐标系如图所示,
则O(0,0,0),B(2,0,0),D(-2,0,0),C(0,2,0),P(0,0,1),
所以DC→=(2,2,0),AB→=2DC→=(4,4,0),
则A(-2,-4,0),
又BC→=(-2,2,0),BP→=(-2,0,1),
设平面PBC的法向量为m→=(x,y,z),
则m→.BC→=-2x+2y=0m→.BP→=-2x+z=0,令x=1,则y=1,z=2,
故m→=(1,1,2),
设平面PAD的法向量为n→=(a,b,c),
因为DP→=(2,0,1),AD→=(0,4,0),
所以n→.DP→=2a+c=0n→.AD→=4b=0,令a=1,则b=0,c=-2,
故n→=(1,0,-2),
所以|cos<m→,n→>|=|n→.m→||n→||m→|=31+1+4×1+4=3010,
故平面PAD与平面PBC所成锐二面角的余弦值为3010.;
【解析】
(1)连接OC,利用勾股定理证明OP⊥OC,又可证明OP⊥BD,根据线面垂直的判定定理证明即可;
(2)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面PBC和平面PAD的法向量,由向量的夹角公式求解即可.
此题主要考查了立体几何的综合应用,涉及了线面垂直的判定定理的应用,二面角的求解,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.
23.【答案】证明:(1)连接QC,
因为AD //BC,BC=12AD,Q为AD的中点,所以QD //BC,QD=BC,
所以四边形BCDQ为平行四边形,所以BQ //CD,BQ=CD=3,
又因为∠ADC=90∘,所以BC⊥BQ;又因为PA=PD,所以PQ⊥AD,
因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PQ⊥平面ABCD,所以PQ⊥QC,PQ⊥BC,
所以BC⊥平面PQB,所以BC⊥PB,
因为M为PC的中点,所以MB=MQ=12PC.
(2)由(1)知PQ⊥平面ABCD,则PB与平面ABCD所成角的平面角为∠PBQ=45∘,所以PQ=BQ=3,则MB=MQ=12PC=12PQ2+QC2=123+22=72,
其中SΔBCQ=12BC⋅QB=32,SΔBQM=12BQ⋅MQ2-(BQ2)2=12⋅3⋅74=32,
又因为M为PC的中点,所以VP-BQM=12VP-BCQ,
设点P到平面MQB的距离为h,
即13⋅SΔBQM⋅h=12⋅13⋅SΔBQC⋅PQ,即h=32,
所以点P到平面MQB的距离为32.;
【解析】此题主要考查面面垂直、直线与平面所成的角,解答本题的关键是掌握相关知识,逐一分析解答即可.
(1)连接QC,因为AD //BC,BC=12AD,Q为AD的中点,所以QD //BC,QD=BC,所以四边形BCDQ为平行四边形,所以BQ //CD,BQ=CD=3,求证MB=MQ;
(2)由(1)知PQ⊥平面ABCD,则PB与平面ABCD所成角的平面角为∠PBQ=45∘,所以PQ=BQ=3,则MB=MQ=12PC=12PQ2+QC2=123+22=72,求点P到平面MQB的距离.
2024年高考数学第一轮复习专题训练第七章 §7.5 空间直线、平面的垂直: 这是一份2024年高考数学第一轮复习专题训练第七章 §7.5 空间直线、平面的垂直,共6页。试卷主要包含了直线和平面所成的角等内容,欢迎下载使用。
2023高考数学复习专项训练《空间直线、平面的平行》: 这是一份2023高考数学复习专项训练《空间直线、平面的平行》,共19页。试卷主要包含了、单选题,、填空题,、解答题等内容,欢迎下载使用。
2023高考数学复习专项训练《空间直线、平面的垂直》: 这是一份2023高考数学复习专项训练《空间直线、平面的垂直》,共19页。试卷主要包含了、单选题,、填空题,、解答题等内容,欢迎下载使用。












