【中考一轮复习】2023年中考数学通用版考点梳理+练习——第12讲　反比例函数及其应用（含答案）

这是一份【中考一轮复习】2023年中考数学通用版考点梳理+练习——第12讲　反比例函数及其应用（含答案），共9页。试卷主要包含了反比例函数的概念，反比例函数的图象与性质等内容，欢迎下载使用。

考 点 清 单
考点1 反比例函数的图象与性质
1．反比例函数的概念
一般地，形如y＝eq \f(k,x)(k为常数，k≠0)的函数，叫做反比例函数．
【注意】(1)反比例函数的表达式除y＝eq \f(k,x)外，还可以写成y＝kx－1或xy＝k(k≠0)；
(2)反比例函数自变量x的取值范围是x≠0；函数y的取值范围是y≠0；
(3)已知点在函数图象上，直接利用xy＝k即可求得k值并确定函数表达式．
2．反比例函数的图象与性质
【注意】因为正比例函数和反比例函数图象都关于原点对称，所以在同一平面直角坐标系中，正比例函数与反比例函数图象若有交点，则两个交点关于原点对称．
【易错警示】双曲线不是连续曲线，是两支不同的曲线，且与坐标轴不相交，所以比较函数值大小时，要注意所判断的点是否在同一象限，当k＞0时，在两支上，第一象限函数值大于第三象限函数值；当k＜0时，在两支上，第二象限函数值大于第四象限函数值．解决这种问题的一个有效办法是画出草图，标出各点，再比较大小．
考点2 反比例函数比例系数k的几何意义
1．k的几何意义
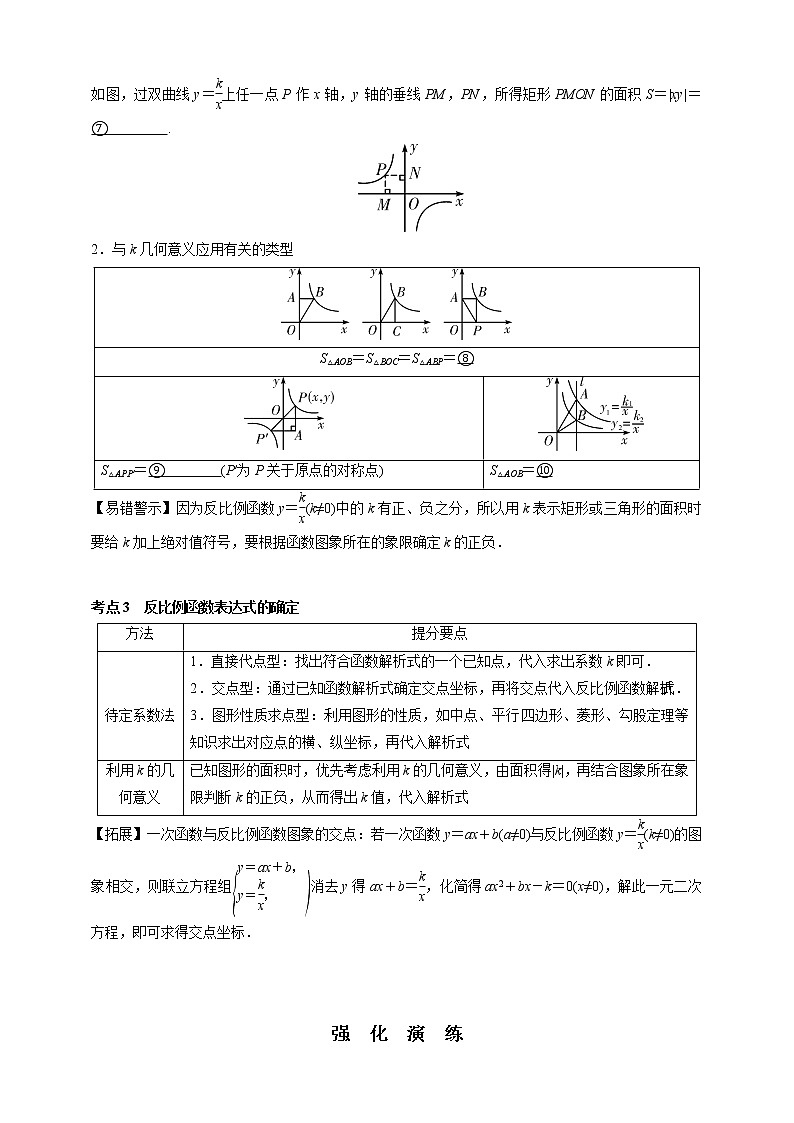
如图，过双曲线y＝eq \f(k,x)上任一点P作x轴，y轴的垂线PM，PN，所得矩形PMON的面积S＝|xy|＝⑦ .
2．与k几何意义应用有关的类型
【易错警示】因为反比例函数y＝eq \f(k,x)(k≠0)中的k有正、负之分，所以用k表示矩形或三角形的面积时要给k加上绝对值符号，要根据函数图象所在的象限确定k的正负．
考点3 反比例函数表达式的确定
【拓展】一次函数与反比例函数图象的交点：若一次函数y＝ax＋b(a≠0)与反比例函数y＝eq \f(k,x)(k≠0)的图象相交，则联立方程组eq \b\lc\{(\a\vs4\al\c1(y＝ax＋b，,y＝\f(k,x)，))消去y得ax＋b＝eq \f(k,x)，化简得ax2＋bx－k＝0(x≠0)，解此一元二次方程，即可求得交点坐标．
强 化 演 练
基础练
1．反比例函数y＝eq \f(k,x)的图象分别位于第二、四象限，则直线y＝kx＋k不经过的象限是( )
A．第一象限 B．第二象限
C．第三象限 D．第四象限
2．已知反比例函数y＝eq \f(k,x)(k≠0)的图象与正比例函数y＝ax(a≠0)的图象相交于A，B两点，若点A的坐标是(1，2)，则点B的坐标是( )
A．(－1，2) B．(1，－2)
C．(－1，－2) D．(2，1)
3．已知反比例函数y＝eq \f(6,x)，则下列描述不正确的是( )
A．图象位于第一、第三象限 B．图象必经过点(4，eq \f(3,2))
C．图象不可能与坐标轴相交 D．y随x的增大而减小
4．函数y＝kx－k与y＝eq \f(k,x)(k≠0)在同一平面直角坐标系中的图象可能是( )

A B C D
5．如图，直线x＝t(t＞0) 与反比例函数y＝eq \f(k,x)(x＞0)，y＝eq \f(－1,x)(x＞0)的图象分别交于B，C两点，A为y轴上任意一点，△ABC的面积为3，则k的值为( )
A．2 B．3 C．4 D．5
6．若点A(－3，y1)，B(－1，y2)，C(2，y3)都在反比例函数y＝eq \f(k,x)(k＜0)的图象上，则y1，y2，y3的大小关系是( )
A．y3＜y1＜y2 B．y2＜y1＜y3 C．y1＜y2＜y3 D．y3＜y2＜y1
7．如图，正比例函数y1＝k1x(k1＜0)的图象与反比例函数y2＝eq \f(k2,x)(k2＜0)的图象相交于A，B两点，点B的横坐标为2，当y1＞y2时，x的取值范围是( )
A．x＜－2或x＞2 B．－2＜x＜0或x＞2
C．x＜－2或0＜x＜2 D．－2＜x＜0或0＜x＜2
8．关于某个函数的表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．
甲：函数图象经过点(－1，1)；
乙：函数图象经过第四象限；
丙：当x＞0时，y随x的增大而增大．
则这个函数的表达式可能是( )
A．y＝－x B．y＝eq \f(1,x) C．y＝x2 D．y＝－eq \f(1,x)
9．已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示．下列说法正确的是( )
A．函数解析式为I＝eq \f(13,R) B．蓄电池的电压是18 V
C．当I≤10 A时，R≥3.6 Ω D．当R＝6 Ω时，I＝4 A
10．如图，在平面直角坐标系中，菱形ABCD的边AD⊥y轴，垂足为E，顶点A在第二象限，顶点B在y轴正半轴上，反比例函数y＝eq \f(k,x)(k≠0，x＞0)的图象同时经过顶点C，D.若点C的横坐标为5，BE＝2DE，则k的值为( )
A．eq \f(40,3) B．eq \f(5,2) C．eq \f(5,4) D．eq \f(20,3)
11．如图，在平面直角坐标系中，点A，B在函数y＝eq \f(k,x)(k＞0，x＞0)的图象上，过点A作x轴的垂线，与函数y＝－eq \f(k,x)(x＞0)的图象交于点C，连接BC交x轴于点D.若点A的横坐标为1，BC＝3BD，则点B的横坐标为( )
A．eq \f(3,2) B．2 C．eq \f(5,2) D．3
12．如图，直线y1＝kx＋1与双曲线y2＝eq \f(2,x)在第一象限交于点P(1，t)，与x轴，y轴分别交于A，B两点，则下列结论错误的是( )
A．t＝2 B．△AOB是等腰直角三角形
C．k＝1 D．当x＞1时，y2＞y1
13．若点A(－3，y1)，B(－4，y2)在反比例函数y＝eq \f(5,x)的图象上，则y1 y2.(填“＞”“＜”或“＝”)
14．如图，A，B两点在反比例函数y＝－eq \f(3,x)(x＜0)的图象上，AB的延长线交x轴于点C，且AB＝2BC，则△AOC的面积是 .
15．如图，矩形ABCD的边AB与y轴平行，顶点A的坐标为(1，2)，点B，D在反比例函数y＝eq \f(6,x)(x＞0)的图象上，点C在反比例函数y＝eq \f(k,x)(x＞0)的图象上，k＝ .
16．已知点A(a，y1)，B(a＋1，y2)在反比例函数y＝eq \f(m2＋1,x)(m是常数)的图象上，且y1＜y2，则a的取值范围是 .
17．如图，将直线y＝x向下平移b个单位长度后得到直线l，l与反比例函数y＝eq \f(5,x)(x＞0)的图象相交于点A，与x轴相交于点B，则OA2－OB2的值为 .
18．如图，点A在x轴正半轴上，B(5，4)，四边形AOCB为平行四边形，反比例函数y＝eq \f(8,x)的图象经过点C，交AB边于点D，则点D的坐标为 .
19．如图，在平面直角坐标系xOy中，直线y＝x＋2与反比例函数y＝eq \f(k,x)(k≠0)的图象交于A，B两点，且点A的坐标为(1，a)．
(1)求a和k的值；
(2)已知点P(m，0)，过点P作平行于y轴的直线，交直线y＝x＋2于点C，交反比例函数y＝eq \f(k,x)(k≠0)的图象于点D.若PC＞PD，结合函数的图象，直接写出m的取值范围．
20．如图，在平面直角坐标系中，菱形ABCD的顶点D在y轴上，A，C两点的坐标分别为(2，0)，(2，m)，直线CD：y1＝ax＋b与双曲线：y2＝eq \f(k,x)交于C，P(－4，－1)两点．
(1)求双曲线y2的函数关系式及m的值；
(2)判断点B是否在双曲线上，并说明理由；
(3)当y1＞y2时，请直接写出x的取值范围．
强化练
21．如图，在△ABC中，C是AB的中点，反比例函数y＝eq \f(k,x)(k＞0)在第一象限的图象经过A，C两点．若△ABO的面积为6，则k的值为( )
A．3 B．4 C．5 D．6
22．已知y1和y2均是以x为自变量的函数，当x＝m时，函数值分别为M1和M2.若存在实数m，使得M1＋M2＝0，则称函数y1和y2具有性质P.以下函数y1和y2具有性质P的是( )
A．y1＝x2＋2x和y2＝－x－1 B．y1＝x2＋2x和y2＝－x＋1
C．y1＝－eq \f(1,x)和y2＝－x－1 D．y1＝－eq \f(1,x)和y2＝－x＋1
23．如图，过反比例函数y＝eq \f(k,x)(k＞0, x＞0)图象上的四点P1，P2，P3，P4分别作x轴的垂线，垂足分别为A1，A2，A3，A4，再过P1，P2，P3，P4分别作y轴的垂线，P1A1，P2A2，P3A3，P4A4构造了四个相邻的矩形．若这四个矩形的面积从左到右依次为S1，S2，S3，S4，OA1＝A1A2＝A2A3＝A3A4，则S1与S4的数量关系为 .
提升练
24．一杠杆装置如图，杆的一端吊起一桶水，水桶对杆的拉力的作用点到支点的杆长固定不变．甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力F甲、F乙、F丙、F丁，将相同重量的水桶吊起同样的高度．若F乙＜F丙＜F甲＜F丁，则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A．甲同学 B．乙同学 C．丙同学 D．丁同学
参 考 答 案
考点清单
①＞ ②＜ ③一、三 ④减小 ⑤二、四 ⑥增大 ⑦|k| ⑧eq \f(|k|,2) ⑨2|k| ⑩eq \f(1,2)(|k1|－|k2|)
强化演练
1. A 2. C 3. D 4. D 5. D 6. A 7. C 8. D 9. C 10. A 11. B 12. D
13. ＜ 14. 6 15. 18 16. －1＜a＜0 17. 10 18. (4，2)
19. 解：(1)∵点A(1，a)在直线y＝x＋2上，∴a＝1＋2＝3，∴点A的坐标为(1，3)．将(1，3)代入y＝eq \f(k,x)，得k＝1×3＝3.
(2)联立eq \b\lc\{(\a\vs4\al\c1(y＝x＋2，,y＝\f(3,x)，))解得eq \b\lc\{(\a\vs4\al\c1(x＝1，,y＝3))或eq \b\lc\{(\a\vs4\al\c1(x＝－3，,y＝－1，))∴B(－3，－1)，如图，由图象可得当m＜－3或m＞1时，PC＞PD.
20. 解：(1)如图，连接AC，BD相交于点E. ∵四边形ABCD是菱形，∴DE＝BE，AE＝CE，AC⊥BD. ∵A(2，0)，C(2，m)，∴E(2，eq \f(1,2)m)，AC∥y轴，∴BD⊥y轴，∴D(0，eq \f(1,2)m)，B(4，eq \f(1,2)m)．∵点C(2，m)，D(0，eq \f(1,2)m)，P(－4，－1)在直线CD上，∴eq \b\lc\{(\a\vs4\al\c1(2a＋b＝m，,b＝\f(1,2)m，,－4a＋b＝－1，))解得eq \b\lc\{(\a\vs4\al\c1(m＝2，,a＝\f(1,2)，,b＝1，))∴C(2，2)．∵点C在双曲线y2＝eq \f(k,x)上，∴k＝2×2＝4，∴双曲线的函数关系式为y2＝eq \f(4,x).
(2)点B在双曲线上，理由如下：由(1)知，m＝2，B(4，eq \f(1,2)m)，∴B(4，1)，由(1)知双曲线的解析式为y2＝eq \f(4,x). ∵4×1＝4，∴点B在双曲线上．
(3)由(1)知C(2，2)，由图知，当y1＞y2时，x的取值范围为－4＜x＜0或x＞2.
21. B 22. A 23. S1＝4S4
24. B
表达式
y＝eq \f(k,x)(k≠0，k为常数)
k的符号
k① 0
k② 0
图象
取值范围
x≠0，y≠0
性质
当k＞0时，函数图象的两个分支分别在第③ 象限，在每个象限内，y随x的增大而④
当k＜0时，函数图象的两个分支分别在第⑤ 象限，在每个象限内，y随x的增大而⑥
对称性
关于原点成中心对称
关于直线y＝x和y＝－x成轴对称
S△AOB＝S△BOC＝S△ABP＝⑧
S△APP′＝⑨ (P′为P关于原点的对称点)
S△AOB＝⑩
方法
提分要点
待定系数法
1．直接代点型：找出符合函数解析式的一个已知点，代入求出系数k即可．
2．交点型：通过已知函数解析式确定交点坐标，再将交点代入反比例函数解析式．
3．图形性质求点型：利用图形的性质，如中点、平行四边形、菱形、勾股定理等知识求出对应点的横、纵坐标，再代入解析式
利用k的几何意义
已知图形的面积时，优先考虑利用k的几何意义，由面积得|k|，再结合图象所在象限判断k的正负，从而得出k值，代入解析式