

2022-2023学年江苏省盐城市七年级下册数学期末专项提升模拟(AB卷)含解析
展开2022-2023学年江苏省盐城市七年级下册数学期末专项提升模拟
(A卷)
一.选一选(共14小题,每小题3分,共42分)
1. 下列各直线的表示法中,正确的是( )
A. 直线ab B. 直线Ab C. 直线A D. 直线AB
2. 下列方程是一元方程的是( )
A. x2=25 B. x﹣5=6 C. x﹣y=6 D. =2
3. 对于直线、射线、线段,在下列各图中能相交的是( )
A. B.
C. D.
4. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A. 1cm B. 9cm C. 1cm或9cm D. 以上答案都没有对
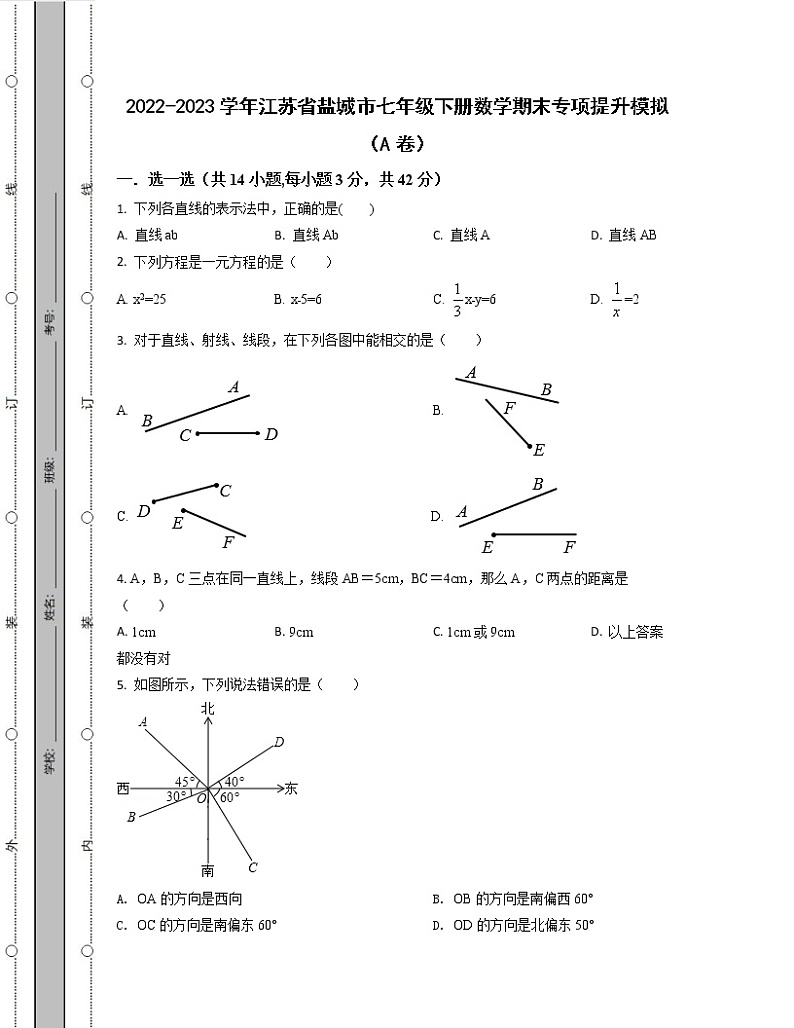
5. 如图所示,下列说法错误的是( )
A. OA的方向是西向 B. OB的方向是南偏西60°
C. OC的方向是南偏东60° D. OD的方向是北偏东50°
6. 学习了角的常用度量单位后,乐乐发现度、分、秒之间可以相互换算,乐乐计算出某一时刻闹钟的时针和分针的夹角是108000″,此时这个夹角等于( )
A 5° B. 15° C. 30° D. 60°
7. 如图,下列表示角的方法,错误的是( )
A. ∠1与∠AOB表示同一个角 B. ∠AOC也可以用∠O来表示
C. ∠β表示的是∠BOC D. 图中共有三个角:∠AOB,∠AOC,∠BOC
8. 如图,从点O出发的五条射线,可以组成( )个角.
A. 4 B. 6 C. 8 D. 10
9. 从某多边形的一个顶点引出的所有对角线把这个多边形分成了6个三角形,则此多边形的形状是( )
A. 六边形 B. 七边形 C. 八边形 D. 九边形
10. 下列等式变形正确的是( )
A. 若,则 B. 若,则
C 若,则 D. 若,则
11. 已知关于x的方程5x+3k=21与5x+3=0的解相同,则k的值是( )
A. ﹣10 B. 7 C. ﹣9 D. 8
12. 方程去分母正确的是( ).
A. x-1-x=-1 B. 4x-1-x=-4 C. 4x-1+x=-4 D. 4x-1+x=-1
13. 如图,点C在线段AB上,点D是AC的中点,如果CB=CD,AB=10.5cm,那么BC的长为( )
A. A2.5cm B. 3cm C. 4.5cm D. 6cm
14. 已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON大小为( )
A. 20° B. 40° C. 20°或40° D. 30°或10°
二.填 空 题(共8小题,每小题3分,共24分)
15. 在2:30时,时钟上的时针和分针之间的夹角为________.
16. 建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,这样做的依据是:__________.
17. 已知线段AB=12,在直线AB上取一点P,恰好使AP=AB,点Q为线段PB的中点,则AQ的长为_____.
18. 如图,点A、O、B一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=___度.
19. 圆心角为120°,半径为2的扇形,则这个扇形的面积为_____.
20. 当=_________时,代数式与的值互为相反数.
21. 某校七年级共有587名学生分别到北京博物馆和中国科技馆参观,其中到北京博物馆人数比到中国科技馆人数的2倍还多56人,设到中国科技馆的人数为x人,可列方程为_____.
22. 一件衣服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元,那么这件衣服的成本是_____元.
三.解 答 题(共6小题)
23. 解方程:
(1)4x=5x﹣5
(2)4x+3(2x﹣3)=12﹣(x﹣4)
(3).
(4)
24. 已知关于x的方程与=3x﹣2的解互为倒数,求m的值.
25. 如图,已知点C为AB上一点,AC=15cm,CB=AC,若D、E分别为AC、AB的中点,求DE的长.
26. 如图,已知∠AOC:∠BOC=1:4,OD平分∠AOB,且∠COD=36°,求∠AOB的度数.
27. 海南五月瓜果飘香,某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
28. 一个自行车队进行训练,训练时所有队员都以相同的速度前进,突然,1号队员以每小时比其他队员快10千米的速度独自行进,行进了10千米后掉转车头,速度没有变往回骑,直到与其他的队员会合.从1号队员离队开始到与其他队员重新会合,了15分钟.
(1)其他队员的行进速度是多少?
(2)1号队员从离队开始到与队员重新会合这个过程中,多长时间与其他队员相距1千米?
2022-2023学年江苏省盐城市七年级下册数学期末专项提升模拟
(A卷)
一.选一选(共14小题,每小题3分,共42分)
1. 下列各直线的表示法中,正确的是( )
A. 直线ab B. 直线Ab C. 直线A D. 直线AB
【正确答案】D
【详解】根据直线的两种表示法:用一个小写字母表示,或用两个大些字母(直线上的)表示,可得选项D正确,故选D.
点睛:本题主要考查了直线的表示法,解题的关键是掌握直线表示法:用一个小写字母表示,或用两个大些字母(直线上的)表示.
2. 下列方程是一元方程的是( )
A. x2=25 B. x﹣5=6 C. x﹣y=6 D. =2
【正确答案】B
【详解】【分析】只含有一个未知数(元),未知数项的次数都是1(次),这样的方程叫做一元方程.据此进行分析.
【详解】
A. x2=25,次数是2,故没有能选;
B. x﹣5=6,符合一元方程条件,故能选;
C. x﹣y=6,含有两个未知数,故没有能选;
D. =2,分母有未知数,是分式方程,故没有能选.
故选B
本题考核知识点:一元方程的意义. 解题关键点:理解一元方程的意义.
3. 对于直线、射线、线段,在下列各图中能相交的是( )
A. B. C. D.
【正确答案】B
【分析】根据直线能向两方无限延伸,射线能向一方无限延伸,线段没有能延伸,据此进行选择.
【详解】A.线段CD没有能延伸,直线延伸方向,与线段无交点,直线和线段没有能相交;
B.射线可以无线延伸,这条射线与这条直线能相交;
C.线段CD没有能延伸,射线EF延伸的方向与线段无交点;
D.直线和射线的延伸方向,得两者没有能相交.
故选B.
本题考查了相交线,理解直线、线段和射线的延伸性是关键.
4. A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A. 1cm B. 9cm C. 1cm或9cm D. 以上答案都没有对
【正确答案】C
【分析】由已知条件知A,B,C三点在同一直线上,做本题时应考虑到A、B、C三点之间的位置,分情况可以求出A,C两点的距离.
【详解】种情况:C点在线段AB上时,故AC=AB-BC=1cm;
第二种情况:当C点在线段AB延长线上时,AC=AB+BC=9cm,
故选C.
5. 如图所示,下列说法错误的是( )
A. OA的方向是西向 B. OB的方向是南偏西60°
C. OC的方向是南偏东60° D. OD的方向是北偏东50°
【正确答案】C
【详解】【分析】图,根据方向角的意义逐个分析.
【详解】
A. OA的方向是西向,说确;
B. OB的方向是南偏西60°,说确;
C. OC的方向是南偏东30°,故说法没有正确;
D. OD的方向是北偏东50°,说确.
故选C
本题考核知识点:方向角. 解题关键点:理解方向角的意义.
6. 学习了角的常用度量单位后,乐乐发现度、分、秒之间可以相互换算,乐乐计算出某一时刻闹钟的时针和分针的夹角是108000″,此时这个夹角等于( )
A. 5° B. 15° C. 30° D. 60°
【正确答案】C
【详解】【分析】根据1度=3600秒,进行转化即可.
【详解】108000″=108000÷3600(度)= 30°
故选C:
本题考核知识点:角度的换算.解题关键点:熟记角度的转换进率.
7. 如图,下列表示角的方法,错误的是( )
A. ∠1与∠AOB表示同一个角 B. ∠AOC也可以用∠O来表示
C. ∠β表示的是∠BOC D. 图中共有三个角:∠AOB,∠AOC,∠BOC
【正确答案】B
【详解】解:由于顶点O处,共有3个角,所以∠AOC没有可以用∠O来表示,故B错误.故选B.
8. 如图,从点O出发的五条射线,可以组成( )个角.
A. 4 B. 6 C. 8 D. 10
【正确答案】D
【详解】【分析】根据公式m=,可求得的个数m. (n表示射线数)
【详解】根据公式m=,可求得m==10(条).
故选D
本题考核知识点:角. 解题关键点:理解规律公式m=.
9. 从某多边形的一个顶点引出的所有对角线把这个多边形分成了6个三角形,则此多边形的形状是( )
A. 六边形 B. 七边形 C. 八边形 D. 九边形
【正确答案】C
【详解】【分析】根据公式m=n-2,可求得多边形边数n.(m表示三角形个数)
【详解】设多边形的边数为n,则
6=n-2,
所以,n=8
故是八边形.
故选C
本题考核知识点:多边形.解题关键点:由多边形的对角线和分成三角形个数的关系推出边数.
10. 下列等式变形正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
【正确答案】B
【分析】根据等式的基本性质1:等式的两边同时加上(或减去)同一个数或同一个整式,所得的结果仍是等式;等式的基本性质2:等式的两边同时乘以(或除以)同一个数(除数没有为零),所得的结果仍是等式,针对每一个选项进行判断即可.
【详解】解:A、若,则x=,故该选项错误;
B、若3(x+1)-2x=1,则3x+3-2x=1,故该选项正确;
C、若,则,故该选项错误;
D、若,则,故该选项错误.
故选B.
本题考查了等式的基本性质.解题的关键是熟练掌握等式的基本性质.
11. 已知关于x的方程5x+3k=21与5x+3=0的解相同,则k的值是( )
A. ﹣10 B. 7 C. ﹣9 D. 8
【正确答案】D
【详解】∵5x+3=0,∴5x=-3,
∵方程5x+3k=24与5x+3=0的解相同,∴-3+3k=21,解得k=8,
故选D.
12. 方程去分母正确的是( ).
A. x-1-x=-1 B. 4x-1-x=-4 C. 4x-1+x=-4 D. 4x-1+x=-1
【正确答案】C
【详解】
方程左右两边各项都要乘以4,故选C
13. 如图,点C在线段AB上,点D是AC的中点,如果CB=CD,AB=10.5cm,那么BC的长为( )
A. A2.5cm B. 3cm C. 4.5cm D. 6cm
【正确答案】C
【详解】【分析】由线段中点定义得AD=CD,由AB=AD+DC+BC得10.5=CD+CD+CD,解得CD,再求BC.
【详解】因为,点D是AC的中点,
所以,AD=CD,
又因为CB=CD,
所以,由AB=AD+DC+BC得10.5=CD+CD+CD,
解得CD=3,
所以,CB=×3=,
故选C
本题考核知识点:线段中点.解题关键点:由线段中点定义得到线段相等,由线段和列出方程.
14. 已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为( )
A. 20° B. 40° C. 20°或40° D. 30°或10°
【正确答案】C
【详解】解:本题需要分两种情况进行讨论,
当射线OC在∠AOB外部时,∠MON=∠BOM+∠BON=30°+10°=40°;
当射线OC在∠AOB内部时,∠MON=∠BOM-∠BON=30°-10°=20°;
故选:C.
本题考查角平分线的性质、角度的计算,注意分类讨论是本题的解题关键.
二.填 空 题(共8小题,每小题3分,共24分)
15. 在2:30时,时钟上的时针和分针之间的夹角为________.
【正确答案】105°
【详解】【分析】这属于时针和分针的追及问题,先计算时针和分针转过的度数,再求出差.
【详解】因为,分针:60分钟转一圈,每分钟转动的角度为:360°÷60=6°;
时针:12小时转一圈,每小时转动的角度为:360°÷12=30°.
所以,在2:30时,时钟上时针和分针之间的夹角为:6°×30-30°×2.5=105°.
故答案为105°
本题考核知识点:钟面角. 解题关键点:熟记时针和分针的转速.
16. 建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,这样做的依据是:__________.
【正确答案】两点确定一条直线
分析】由直线公理可直接得出答案.
【详解】建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故两点确定一条直线.
本题主要考查的是直线的性质,掌握直线的性质是解题的关键.
17. 已知线段AB=12,在直线AB上取一点P,恰好使AP=AB,点Q为线段PB的中点,则AQ的长为_____.
【正确答案】4或8
【详解】当点P在点A的左侧时,如右图1所示,
∵线段AB=12,在直线AB上取一点P,恰好使AP=AB,点Q为线段PB的中点,
∴AP=4,
∴PB=PA+AB=16,
∴PQ=8,
∴AQ=PQ﹣PA=4,
当点P在点A的右侧时,如右图2所示,
∵线段AB=12,在直线AB上取一点P,恰好使AP=AB,点Q为线段PB的中点,
∴AP=4,
∴PB=AB﹣AP=8,
∴PQ=4,
∴AQ=AP+PQ=8,
故答案为4或8.
18. 如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=___度.
【正确答案】155
【详解】试题分析:因为点A、O、B在一条直线上,且∠AOC=50°,所以∠BOC=130°,又OD平分∠AOC,所以∠DOC=∠AOC=25°,所以∠BOD=∠BOC+∠DOC =130°+25°=155°.
考点:1.角的平分线2.角的和差关系3.角的计算.
19. 圆心角为120°,半径为2的扇形,则这个扇形的面积为_____.
【正确答案】
【详解】【分析】由扇形面积公式S=,可求得面积.
【详解】由扇形面积公式S=,可求得S=
故答案为
本题考核知识点:扇形面积. 解题关键点:熟记扇形面积公式.
20. 当=_________时,代数式与的值互为相反数.
【正确答案】1
【详解】试题解析:根据题意列方程:2x+1=5x-8,
移项,合并同类项得
-3x=-9,
系数化为1,得x=3.
考点:解一元方程.
21. 某校七年级共有587名学生分别到北京博物馆和中国科技馆参观,其中到北京博物馆的人数比到中国科技馆人数的2倍还多56人,设到中国科技馆的人数为x人,可列方程为_____.
【正确答案】x+2x+56=587.
【详解】试题分析:由到中国科技馆的人数为x人可得到北京博物馆的人数为2x+56,再根据七年级共有589名学生列出方程即可
解:设到中国科技馆的人数为x人,依题意可列方程为:
x+2x+56=589,
故答案为x+2x+56=589.
考点:由实际问题抽象出一元方程.
22. 一件衣服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元,那么这件衣服的成本是_____元.
【正确答案】140
【详解】解:设这件衣服的成本是x元,根据题意得:
x(1+50%)×80%﹣x=28,
解得:x=140.
答:这件衣服成本是140元;
故答案为140.
三.解 答 题(共6小题)
23. 解方程:
(1)4x=5x﹣5
(2)4x+3(2x﹣3)=12﹣(x﹣4)
(3).
(4)
【正确答案】(1) x=5;(2) x=;(3) x=0;(4) x=1.
【分析】根据解方程一般步骤可得.即:去分母,去括号,移项,合并同类项,系数化为1.
【详解】解:(1)4x=5x﹣5
4x﹣5x=﹣5,
则﹣x=﹣5,
解得:x=5;
解:(2)去括号得,4x+6x﹣9=12﹣x+4,
移项得,4x+6x+x=12+4+9,
合并同类项得,11x=25,
系数化为1得,x=;
解:(3)﹣1=
去分母得:3(x+2)﹣12=2(2x﹣3),
去括号得:3x+6﹣12=4x﹣6,
移项得:3x﹣4x=﹣6﹣6+12,
合并同类项得:-x=0
系数化为1得:x=0.
解:(4)去分母得,4(2x﹣1)﹣2(10x+1)=3(2x+1)﹣27,
去括号得,8x﹣4﹣20x﹣2=6x+3﹣27,
移项得,8x﹣20x﹣6x=3﹣27+4+2,
合并同类项得,﹣18x=﹣18,
系数化为1得,x=1.
本题考核知识点:解一元方程. 解题关键点:熟记解一元方程的一般步骤.
24. 已知关于x的方程与=3x﹣2的解互为倒数,求m的值.
【正确答案】
【详解】解方程,可得x=1,由于解互为倒数,把x=1代入可得,可得,解得m=-.
故答案为-.
点睛:此题主要考查了一元方程解,利用同解方程,可先求出一个方程的解,再代入第二个含有m的方程,从而求出m即可.
25. 如图,已知点C为AB上一点,AC=15cm,CB=AC,若D、E分别为AC、AB的中点,求DE的长.
【正确答案】
【分析】根据条件可求出AB与CD的长度,利用中点的性质即可求出AE与AD的长度,从而可求出答案.
【详解】解:∵AC=15 cm,CB=AC,∴CB=10 cm,AB=15+10=25 cm.
又∵E是AB的中点,D是AC的中点,∴AE=AB=12.5 cm.
∴AD=AC=7.5 cm,∴DE=AE﹣AD=12.5﹣7.5=5 cm.
本题考查了两点间的距离,解题的关键是熟练运用线段之间的熟练关系,本题属于基础题型.
26. 如图,已知∠AOC:∠BOC=1:4,OD平分∠AOB,且∠COD=36°,求∠AOB的度数.
【正确答案】120°
【详解】设∠AOC=x°,则∠BOC、∠AOB、∠AOD均可用x表示出来,由∠COD=36°来列方程,求x.
解:设∠AOC=x°,则∠BOC=4x°.
∵OD平分∠AOB,
∴∠AOD=∠AOB= (x°+4x°)=2.5x°.
又∵∠COD=∠AOD-∠AOC,
∴2.5x°-x°=36°.x=24.
∴∠AOB=∠AOC+∠BOC=x°+4x°=120°.
27. 海南五月瓜果飘香,某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
【正确答案】李叔叔购买“无核荔枝”12千克,购买“鸡蛋芒果”18千克.
【分析】设李叔叔购买“无核荔枝”x千克,购买“鸡蛋芒果”y千克,根据总质量为30千克,总花费为708元,可得出方程组,解出即可.
【详解】解:设李叔叔购买“无核荔枝” x千克,购买“鸡蛋芒果” y千克,
由题意,得:,解得:.
答:李叔叔购买“无核荔枝”12千克,购买“鸡蛋芒果”18千克.
28. 一个自行车队进行训练,训练时所有队员都以相同的速度前进,突然,1号队员以每小时比其他队员快10千米的速度独自行进,行进了10千米后掉转车头,速度没有变往回骑,直到与其他的队员会合.从1号队员离队开始到与其他队员重新会合,了15分钟.
(1)其他队员的行进速度是多少?
(2)1号队员从离队开始到与队员重新会合这个过程中,多长时间与其他队员相距1千米?
【正确答案】(1) 其他队员的行进速度是35千米/小时.(2) 小时或小时长时间与其他队员相距1千米.
【详解】【分析】(1)设其他队员的行进速度是x千米/小时,根据15分钟内,两者路程和为10千米×2,得x+(x+10)=10×2;(2)分两种情况分析:离开时和返回时.
【详解】解:(1)设其他队员的行进速度是x千米/小时,依题意有
x+(x+10)=10×2,
解得x=35.
故其他队员的行进速度是35千米/小时.
(2)设y小时长时间与其他队员相距1千米,依题意有
①35y+1=(35+10)y,
解得:x=;
②35y+(35+10)y=10×2﹣1,
解得:y=.
答:小时或.
小时长时间与其他队员相距1千米.
本题考核知识点:列方程解应用题. 解题关键点:根据路程关系列出方程.
2022-2023学年江苏省盐城市七年级下册数学期末专项提升模拟
(B卷)
一、填 空 题(每小题3分,共30分)
1. 太阳半径约为696000千米,数字696000用科学记数法表示为_______千米.
2. 近似数5.3万到_______位.把234.0615四舍五入到千分位,近似数是________.
3. 吐鲁番盆地低于海平面155米,记作﹣155m,南岳衡山高于海平面1900米,则衡山比吐鲁番盆地高_____m.
4. -4的倒数是________,相反数是_______.值是_________.
5. 最小的正整数是________,的负整数是_______,值最小的数是________.
6. 一个数的倒数是它本身,这个数是_______, 互为倒数的两个数的_______是1,一个数的相反数是它本身这个数是________.
7. 若单项式5x4y和5xnym是同类项,则m+n的值是_______.
8. 如果|a-4|+|b+5|=0,则a+b=_______,a-b=_______,a×b=________.
9. 38°41′的角的余角等于________,123°59′的角的补角等于________.
10. 若|a| =|b|,则a 与b的关系是__________________________..
二.选一选(每题3分,共30分)
11. 如果两个有理数、互为相反数,则、一定满足的关系为( )
A. B. C. D.
12. 设、、为三个有理数,下列等式成立是( )
A. B.
C. D.
13. 多项式-23m2-n2是( )
A 二次二项式 B. 三次二项式 C. 四次二项式 D. 五次二项式
14. 我国某年石油产量约为170000000吨,用科学记数法表示为( )
A. 1.7×10-7吨 B. 1.7×107吨 C. 1.7×108吨 D. 1.7×109吨
15. 已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A. 7 B. 4 C. 1 D. 没有能确定
16. 单项式系数是( )
A. -3 B. - C. - D.
17. 已知轮船在逆水中前进的速度是m千米/时,水流的速度是3千米/时,则这轮船在静水中航行的速度是( ).
A. (m-3)千米/时 B. (m+3)千米/时 C. (3-m)千米/时 D. 以上答案都没有对
18. 若原产量为n吨,增产30%后的产量为( )
A. 30%n吨 B. (1﹣30%)n吨 C. (1+30%)n吨 D. (n+30%)吨
19. 如果从A看B的方向为北偏东,那么从B看A的方向为( )
A 南偏东65° B. 南偏西65° C. 南偏东25° D. 南偏西25°
20. 已知线段AB=6cm,在直线AB上画线段AC=2,则BC的长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 没有能确定
三.解 答 题(共计60分)
21. 已知|x-|+(2y+1)2=0,求x2+y2的值是多少?
22. 计算题
(1). +16÷( ) (2).(-24)×() +
(3). (4)
23. 已知:a,b互为相反数,c,d互为倒数,x2=9,求:x-(a+b-cd)3的值.
24. 在对某班的数学测试成绩进行统计分析中,各分数段的人数如图所示(分数取整数,满分100分)根据图形回答下列问题:
(1)该班有多少名学生?
(2)该班这次数学测试及格率(60分以上为及格)是多少?( 结果保留十分位)
25. 一只小虫从某点P出发,在一条直线上来回爬行,假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:+5,﹣3,+10,﹣8,﹣6,+12,﹣10.
(1)通过计算说明小虫是否回到起点P.
(2)如果小虫爬行的速度为0.5厘米/秒,那么小虫共爬行了多长时间.
26. 如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
2022-2023学年江苏省盐城市七年级下册数学期末专项提升模拟
(B卷)
一、填 空 题(每小题3分,共30分)
1. 太阳半径约696000千米,数字696000用科学记数法表示为_______千米.
【正确答案】 .
【详解】试题分析:696000=6.96×105,故答案为6.96×105.
考点:科学记数法—表示较大的数.
2. 近似数5.3万到_______位.把234.0615四舍五入到千分位,近似数是________.
【正确答案】 ①. 千, ②. 234.062,
【详解】分析:到哪一位是看的一个数所在的位置.四舍五入看位数的后一位,如果大于等于5,则需要进一,比5小则舍去.
详解:近似数5.3万到千位;把234.0615四舍五入到千分位,近似数是234.062.
点睛:本题主要考查的是近似数,属于基础题型.理解表达方式是解题的关键.
3. 吐鲁番盆地低于海平面155米,记作﹣155m,南岳衡山高于海平面1900米,则衡山比吐鲁番盆地高_____m.
【正确答案】2055
【详解】试题分析:根据正负数的意义,把比海平面低记作“﹣”,则比海平面高可记作“+”,求高度差用“作差法”,列式计算.
解:吐鲁番盆地低于海平面155米,记作﹣155m,则南岳衡山高于海平面1900米,记作+1900米;
∴衡山比吐鲁番盆地高1900﹣(﹣155)=2055(米).
考点:正数和负数.
4. -4的倒数是________,相反数是_______.值是_________.
【正确答案】 ①. -, ②. 4, ③. 4;
【详解】分析:当两数的积为1时,则两数互为倒数;当两数的和为零时,则两数互为相反数;负数的值等于它的相反数.
详解:-4的倒数是;相反数是4;值是4.
点睛:本题主要考查是倒数、相反数、值的定义,属于基础题型.理解定义是解题的关键.
5. 最小的正整数是________,的负整数是_______,值最小的数是________.
【正确答案】 ①. 1 ②. -1 ③. 0
【详解】分析:根据正整数、负整数和值的性质即可求解.
详解:最小的正整数是1,的负整数是-1,值最小的数是0.
点睛:本题主要考查的是有理数的性质,属于基础题型.理解整数及值的性质得出答案.
6. 一个数的倒数是它本身,这个数是_______, 互为倒数的两个数的_______是1,一个数的相反数是它本身这个数是________.
【正确答案】 ①. 1或-1, ②. 积, ③. 0;
【详解】分析:倒数等于本身的数为1和-1,相反数等于本身的数为0.
详解:一个数的倒数是它本身,这个数是1和-1,互为倒数的两个数的积是1,一个数的相反数是它本身这个数是0.
点睛:本题主要考查的是倒数和相反数的性质,属于基础题型.理解定义是解题的关键.
7. 若单项式5x4y和5xnym是同类项,则m+n的值是_______.
【正确答案】5;
【详解】分析:同类项是指所含的字母相同,且相同字母的指数也相同的单项式.根据定义可以得出m和n的值,从而得出答案.
详解:根据定义可得:m=1,n=4,则m+n=5.
点睛:本题主要考查的是同类项的定义,属于基础题型.理解同类项的定义是解决这个问题的关键.
8. 如果|a-4|+|b+5|=0,则a+b=_______,a-b=_______,a×b=________.
【正确答案】 ①. -1 , ②. 9, ③. -20;
【详解】分析:根据值的非负性分别求出a和b的值,从而得出答案.
详解:∵, ∴a-4=0,b+5=0, 解得:a=4,b=-5,
∴a+b=-1,a-b=9,a×b=-20.
点睛:本题主要考查的是值的性质,属于基础题型.几个非负数的和为零,则每一个非负数都为零.理解这个性质是解题的关键.
9. 38°41′的角的余角等于________,123°59′的角的补角等于________.
【正确答案】 ①. 51°19′ ②. 56°1′.
【详解】38°41′的角的余角=90°−38°41′=51°19′
123°59′的角的补角=180°−123°59′=56°1′
故51°19′、56°1′.
10. 若|a| =|b|,则a 与b的关系是__________________________..
【正确答案】a=b或a+b=0
【详解】分析:互为相反数的两个数的值相等.
详解:∵, ∴a=±b, 即a=b或a+b=0.
点睛:本题主要考查的是值的性质,属于基础题型.相等的两数的值相等,互为相反数的两个数的值相等.
二.选一选(每题3分,共30分)
11. 如果两个有理数、互为相反数,则、一定满足的关系为( )
A. B. C. D.
【正确答案】C
【详解】互为相反数的两个数相加得0,所以a+b=0.
故选C.
12. 设、、为三个有理数,下列等式成立的是( )
A. B.
C. D.
【正确答案】D
详解】A选项错误,a(b+c)=ab+ac.
B选项错误,(a+b)·c=ac+bc.
C选项错误,(a-b)·c=ac-bc.
D选项正确.
故选D.
点睛:熟练掌握乘法分配律.
13. 多项式-23m2-n2是( )
A. 二次二项式 B. 三次二项式 C. 四次二项式 D. 五次二项式
【正确答案】A
【详解】分析:多项式中各单项式的次数作为多项式的次数,单项式的个数为多项式的项数.
详解:是二次二项式, 故选A.
点睛:本题主要考查的是多项式的次数和项数,属于基础题型.理解多项式的定义是解题的关键.
14. 我国某年石油产量约为170000000吨,用科学记数法表示为( )
A. 1.7×10-7吨 B. 1.7×107吨 C. 1.7×108吨 D. 1.7×109吨
【正确答案】C
【详解】分析:科学记数法的表示值大于1的数的方法:a×,且,n为原数的整数位数减一.
详解:170000000=1.7×,故选C.
点睛:本题主要考查的是用科学记数法表示较大的数,属于基础题型.理解科学记数法是解题的关键.
15. 已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A. 7 B. 4 C. 1 D. 没有能确定
【正确答案】A
【分析】观察题中的代数式2x+4y+1,可以发现2x+4y+1=2(x+2y)+1,因此可整体代入,即可求得结果.
【详解】由题意得,x+2y=3,
∴2x+4y+1=2(x+2y)+1=2×3+1=7.
故选A.
本题主要考查了代数式求值,整体代入是解答此题的关键.
16. 单项式的系数是( )
A. -3 B. - C. - D.
【正确答案】C
【详解】分析:单项式的系数是指单项式中的数字因数;所有字母的指数之和为单项式的次数.
详解:根据定义可得单项式的系数为:, 故选C.
点睛:本题主要考查的是单项式的系数,属于基础题型.理解定义是解决这个问题的关键.
17. 已知轮船在逆水中前进的速度是m千米/时,水流的速度是3千米/时,则这轮船在静水中航行的速度是( ).
A. (m-3)千米/时 B. (m+3)千米/时 C. (3-m)千米/时 D. 以上答案都没有对
【正确答案】B
【详解】分析:逆水速度=船速-水速,顺水速度=船速+水速.
详解:设静水的速度为x千米/时,根据题意可得:x-3=m,解得:x=(m+3)千米/时,故选B.
点睛:本题主要考查的是一元方程的应用,属于基础题型.解决这个问题必须要明白逆水速度=船速-水速这个公式.
18. 若原产量为n吨,增产30%后的产量为( )
A. 30%n吨 B. (1﹣30%)n吨 C. (1+30%)n吨 D. (n+30%)吨
【正确答案】C
【分析】根据增产量=原产量×(1+增长率)作答.
【详解】若原产量为n吨,增产30%后的产量为(1+30%)n吨.
故选:C.
19. 如果从A看B的方向为北偏东,那么从B看A的方向为( )
A. 南偏东65° B. 南偏西65° C. 南偏东25° D. 南偏西25°
【正确答案】D
【详解】分析:根据题意画出图形,再根据方位角的表示方法进行解答即可.
详解:如图所示:
∵从点A看点B的方向为北偏东25°, ∴∠1=∠2=25°,∠3=90°-∠2=90°-25°=65°,
∴从点B看点A方向为:南偏西25°或西偏南65°.故选D.
点睛:本题考查的是方向角的概念,根据题意画出图形,再根据方向角的表示方法进行解答即可.
20. 已知线段AB=6cm,在直线AB上画线段AC=2,则BC的长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 没有能确定
【正确答案】C
【详解】分析:画出图形,分情况讨论:①当点C在线段AB上;②当点C在线段BA的延长线上;③因为AB大于AC,所以点C没有可能在AB的延长线上.
详解:如图所示,可知:①当点C在线段AB上时,BC=AB-AC=4;②当点C在线段BA的延长线上时,BC=AB+AC=8.故选C.
点睛:本题主要考查的是线段的长度计算,属于基础题型.注意根据题意,分情况讨论,要画出正确的图形,图形进行计算.
三.解 答 题(共计60分)
21. 已知|x-|+(2y+1)2=0,求x2+y2的值是多少?
【正确答案】
【详解】分析:根据非负数之和为零可知每一个非负数都为零,根据题意得出x和y的值,然后代入进行计算得出答案.
详解:∵ ︳x-︳≥0,≥0,且︳x-︳+=0
∴x-=0且2y+1=0 ∴x=, y=- ∴+=+=.
点睛:本题主要考查的是非负数的性质,属于基础题型.几个非负数的和为零,则每一个非负数都为零,初中阶段所学的非负数为算术平方根、值和平方.
22. 计算题
(1). +16÷( ) (2).(-24)×() +
(3). (4)
【正确答案】(1)-;(2)-9 ;(3)-8ab (4)
【详解】分析:(1)、首先计算乘除法,然后进行加法计算;(2)、利用乘法分配律进行简便计算得出答案;(3)、首先根据单项式乘以多项式的法则将括号去掉,然后进行合并同类项得出答案;(4)、根据有理数的混合计算法则得出答案.
详解:(1)、原式=;
(2)、原式=(-24)×-(-24)×+(-24)×+(-8)=-3+8-6-8=-9;
(3)、原式=15-5-3-15=-8;
(4)、原式=-9+=.
点睛:本题主要考查的是有理数的混合计算法则以及合并同类项计算,属于基础题型.理解计算法则是解题的关键.
23. 已知:a,b互为相反数,c,d互为倒数,x2=9,求:x-(a+b-cd)3的值.
【正确答案】(1)4;(2)-2
【详解】分析:根据相反数和倒数的性质得出a+b=0,cd=1,根据平方根的性质得出x=±3,然后分两种情况得出答案.
详解:由已知得,a+b=0,cd=1,x=3或-3,
(1)、当x=3时,原式=3-(0-1)=4,
(2)、当x=-3时,原式=-3-(0-1)=-2.
点睛:本题主要考查的是相反数、倒数和平方根的计算,属于基础题型.理解他们的性质是解题的关键.
24. 在对某班的数学测试成绩进行统计分析中,各分数段的人数如图所示(分数取整数,满分100分)根据图形回答下列问题:
(1)该班有多少名学生?
(2)该班这次数学测试的及格率(60分以上为及格)是多少?( 结果保留十分位)
【正确答案】(1) 这个班共有60人;(2) 767﹪
【详解】分析:(1)、将各组的人数进行求和得出答案;(2)、首先求出60分以上的人数,然后除以总人数得出答案.
详解:(1)、6+8+10+18+16+2=60(人), 答:这个班共有60人.
(2)、(10+18+16+2)÷60≈76.7﹪.
点睛:本题主要考查的是条形统计图的性质,属于基础题型.理解条形统计图的含义是解题的关键.
25. 一只小虫从某点P出发,在一条直线上来回爬行,假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:+5,﹣3,+10,﹣8,﹣6,+12,﹣10.
(1)通过计算说明小虫是否回到起点P.
(2)如果小虫爬行的速度为0.5厘米/秒,那么小虫共爬行了多长时间.
【正确答案】(1)小虫回到了起点P;(2)小虫共爬行了108秒.
【分析】(1)、将各数进行相加得出结果为0,即回到了原点;(2)、首先将各数的值进行相加,然后除以速度得出答案.
【详解】(1)5+(-3)+10+(-8)+(-6)+12+(-10)=0,
答:小虫回到了原点.
(2)︳5 ︳+ ︳-3︳+ ︳10︳+︳-8︳+︳-6︳+︳12︳+︳-10︳=54(厘米)
54÷0.5=108(秒),
答:小虫共爬行了108秒.
本题主要考查的是有理数加法的实际应用,属于基础题型.理解题目的含义是解题的关键,什么时候需要进行值相加是难点.
26. 如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
【正确答案】80°
【分析】设∠BOE=x°,则∠EOC=2x°,由∠DOE=70°,OD平分∠AOB知,∠AOD=∠DOB=70°﹣x°,再根据∠AOD+∠DOB+∠BOE+∠EOC=180°,列出关于x的方程求解即可.
【详解】解:如图,设∠BOE=x°,
∵∠BOE=∠EOC,
∴∠EOC=2x°,
∵OD平分∠AOB,
∴∠AOD=∠DOB=70°﹣x°,
∵∠AOD+∠DOB+∠BOE+∠EOC=180°,
∴70°﹣x°+70°﹣x°+x°+2x°=180°,
∴x°=40°,
∴∠EOC=80°.
本题主要考查角的计算及角平分线的定义,熟练掌握角平分线的定义及性质是解题的关键.
2022-2023学年江苏省南京市七年级下册数学专项提升模拟卷(AB卷)含解析: 这是一份2022-2023学年江苏省南京市七年级下册数学专项提升模拟卷(AB卷)含解析,共41页。
2022-2023学年江苏省盐城市七年级下册数学期中专项提升模拟(AB卷)含解析: 这是一份2022-2023学年江苏省盐城市七年级下册数学期中专项提升模拟(AB卷)含解析,共42页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年江苏省盐城市七年级下册数学期末专项突破模拟(AB卷)含解析: 这是一份2022-2023学年江苏省盐城市七年级下册数学期末专项突破模拟(AB卷)含解析,共51页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












