2022-2023学年湖北省黄冈市八年级下册数学期末专项提升模拟题（AB卷）含解析

这是一份2022-2023学年湖北省黄冈市八年级下册数学期末专项提升模拟题（AB卷）含解析，共41页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年湖北省黄冈市八年级下册数学期末专项提升模拟题（A卷）
一、选一选：（每小题4分，共40分．请将正确答案的字母填写在表格内）
1. 下列图形是轴对称图形有（　　）

A. 1个 B. 2个 C. 3个 D. 4个
2. 如图，在折纸中，小明制作了一张△ABC纸片，D，E分别是边AB，AC上的点，将△ABC沿着DE折叠压平，点A与点A′重合，若∠A＝70°，则∠1＋∠2的度数为(　　)

A. 110° B. 140° C. 220° D. 70°

3. 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是(　　)

A. 50° B. 60° C. 100° D. 120°
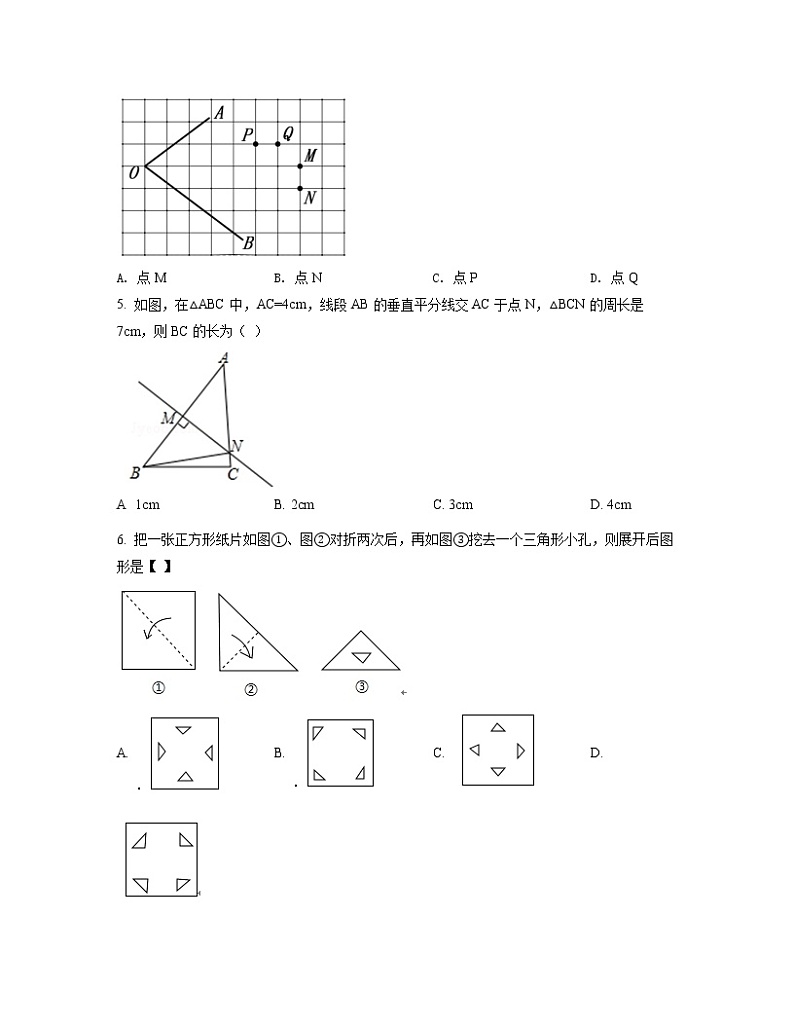
4. 在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是（ ）

A. 点M B. 点N C. 点P D. 点Q
5. 如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（ ）

A 1cm B. 2cm C. 3cm D. 4cm
6. 把一张正方形纸片如图①、图②对折两次后，再如图③挖去一个三角形小孔，则展开后图形是【 】

A. B. C. D.
7. （x－m）2＝x2＋nx＋36，则n的值为（　　）
A. 12 B. －12 C. －6 D. ±12
8. 如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案．已知该图案的面积为49，小正方形的面积为4，若用x、y表示小矩形的两边长(x＞y)，请观察图案，指出以下关系式中没有正确的是 ( )


A. B.
C. D.
9. 解分式方程分以下四步，其中错误的一步是（ ）
A. 方程两边分式最简公分母是
B. 方程两边都乘以，得整式方程
C. 解这个整式方程，得
D. 原方程的解为
10. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原来计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（　　）
A. B.
C. D.
二、填 空 题：（每小题4分，共20分）
11. 如图，在△ABC中，∠B＝42°，△ABC的外角∠DAC和∠ACF的平分线交于点E，则∠AEC＝____________．

12. 如图，△ABC和△FDE中，AD=FC，AB=EF，当添加条件_______时，就可得到△ABC≌△FED．（只需填写一个正确条件即可）

13. 如图所示，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，若DE＝2，则EC＝_________．

14. 某种电子元件的面积大约为0.00000069平方毫米，将0.00000069这个数用科学记数法表示为______．
15. 若关于x的方程无解，则m=_____．
三、解 答 题：（共90分）
16. （1）计算：5a3b·（－3b）2＋（－ab）（－6ab）2；
（2）先化简（a2b－2ab2－b3）÷b－（a＋b）（a－b），然后对式子中a、b分别选择一个自己最喜欢的数代入求值．
（3）解方程.
17. 已知，求的值．
18. 如图是由三个阴影的小正方形组成的图形，请你在三个网格图中，各补画出一个有阴影的小正方形，使补画后的图形为轴对称图形．

19. 如图所示，求∠A＋∠B＋∠C＋∠D＋∠E．

20. 如图所示，若 MP和 NQ 分别垂直平分AB和 AC．
（1）若△APQ的周长为12，求 BC的长；
（2）∠BAC=105°，求∠PAQ 的度数．

21. 有一项工程，若甲队单独做，恰好在规定日期完成，若乙队单独做要超过规定日期3天完成；现在先由甲、乙两队合做2天后，剩下的工程再由乙队单独做，也刚好在规定日期完成，问规定日期多少天？
22. 已知：∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D. 求证：PC=PD.

23. （1）阅读理解：
如图 1，在△ABC 中，若 AB=10，AC=6，求 BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长 AD到点 E使 DE=AD，连接 BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把 AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线 AD的取值范围是__________.
（2）问题解决：如图2，在△ABC中，D是 BC边上的中点,DE⊥DF 于点 D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．


















2022-2023学年湖北省黄冈市八年级下册数学期末专项提升模拟题（A卷）
一、选一选：（每小题4分，共40分．请将正确答案的字母填写在表格内）
1. 下列图形是轴对称图形的有（　　）

A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】D

【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．
【详解】个图有1条对称轴，是轴对称图形，符合题意；
第二个图没有是轴对称图形，因为找没有到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即没有满足轴对称图形的定义，没有符合题意；
第三个图有2条对称轴，是轴对称图形，符合题意；
第四个图有5条对称轴，是轴对称图形，符合题意；
第五个图有1条对称轴，是轴对称图形，符合题意；
第六个图没有是轴对称图形，因为找没有到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即没有满足轴对称图形的定义，没有符合题意.
故轴对称图形有4个.
故选D.
本题考查的是轴对称图形，熟练掌握它的概念是解题的关键.
2. 如图，在折纸中，小明制作了一张△ABC纸片，D，E分别是边AB，AC上的点，将△ABC沿着DE折叠压平，点A与点A′重合，若∠A＝70°，则∠1＋∠2的度数为(　　)

A. 110° B. 140° C. 220° D. 70°
【正确答案】B

【分析】根据三角形的内角和等于180°求出∠ADE+∠AED，再根据翻折变换的性质可得∠A′DE=∠ADE，∠A′ED=∠AED，然后利用平角等于180°列式计算即可得解．
【详解】解：∵∠A=70°，
∴∠ADE+∠AED=180°-70°=110°，
∵△ABC沿着DE折叠压平，A与A′重合，
∴∠A′DE=∠ADE，∠A′ED=∠AED，
∴

故选：B．
本题考查了三角形的内角和定理，翻折变换的性质，解题的关键是利用翻折的性质找到相等的角．

3. 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是(　　)

A 50° B. 60° C. 100° D. 120°
【正确答案】A

【详解】根据全等三角形性质求出∠B=∠EDF=20°和∠C=∠F =60°，根据三角形内角和定理求出∠BAC=180°﹣∠B﹣∠C=100°，根据角平分线定义求出∠DAC=∠BAC=50°，
故选A．
点睛：此题主要考查了全等三角形的性质，三角形的内角和定理，角平分线的定义，能根据全等三角形的性质求出∠B和∠C是解题关键.
4. 在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是（ ）

A. 点M B. 点N C. 点P D. 点Q
【正确答案】A

【分析】利用到角的两边的距离相等的点在角的平分线上进行判断．
【详解】点P、Q、M、N中在∠AOB的平分线上的是M点．
故选：A．
本题主要考查了角平分线的性质，根据正方形网格看出∠AOB平分线上的点是解答问题的关键．
5. 如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（ ）

A. 1cm B. 2cm C. 3cm D. 4cm
【正确答案】C

【详解】试题分析：∵MN是线段AB的垂直平分线，∴AN=BN，∵△BCN的周长是7cm，∴BN+NC+BC=7（cm），∴AN+NC+BC=7（cm），∵AN+NC=AC，∴AC+BC=7（cm），又∵AC=4cm，∴BC=7﹣4=3（cm）．故选C．
考点：线段垂直平分线的性质．
6. 把一张正方形纸片如图①、图②对折两次后，再如图③挖去一个三角形小孔，则展开后图形是【 】

A. B. C. D.
【正确答案】C

【详解】当正方形纸片两次沿对角线对折成为一直角三角形时，在直角三角形中间的位置上剪三角形，则直角顶点处完好，即原正方形中间无损，且三角形关于对角线对称，三角形的一个顶点对着正方形的边．
故选C．
7. （x－m）2＝x2＋nx＋36，则n的值为（　　）
A. 12 B. －12 C. －6 D. ±12
【正确答案】D

【详解】 （x－m）2＝x2＋nx＋36，


解得：
故选D.
8. 如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案．已知该图案的面积为49，小正方形的面积为4，若用x、y表示小矩形的两边长(x＞y)，请观察图案，指出以下关系式中没有正确的是 ( )


A. B.
C. D.
【正确答案】D

【详解】试题解析：A. 因为正方形图案的边长7,同时还可用(x+y)来表示，故x+y=7正确；
B. 因为正方形图案面积从整体看是49，
从组合来看,可以是,还可以是(4xy+4)，
所以有
即
所以
即x−y=2；
C. 由B可知4xy+4=49. 
D.
故是错误的；
故选D.
9. 解分式方程分以下四步，其中错误的一步是（ ）
A. 方程两边分式的最简公分母是
B. 方程两边都乘以，得整式方程
C. 解这个整式方程，得
D. 原方程的解为
【正确答案】D

【分析】分式方程两边乘以最简公分母，去分母转化为整式方程，求出整式方程的解，经检验即可得到分式方程的解．
【详解】解：分式方程的最简公分母为（x−1）（x＋1），
方程两边乘以（x−1）（x＋1），得整式方程2（x−1）＋3（x＋1）＝6，
解得：x＝1，
经检验x＝1是增根，分式方程无解．
故选：D．
此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
10. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原来计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（　　）
A. B.
C. D.
【正确答案】B

【分析】设原计划每天铺设x米，则实际施工时每天铺设（x+50）米，根据：原计划所用时间-实际所用时间=2，列出方程即可．
【详解】设原计划每天施工x米，则实际每天施工（x+50）米，
根据题意，可列方程：=2，
故选B．
本题考查了由实际问题抽象出分式方程，解题的关键是读懂题意，找出合适的等量关系，列出方程．
二、填 空 题：（每小题4分，共20分）
11. 如图，在△ABC中，∠B＝42°，△ABC的外角∠DAC和∠ACF的平分线交于点E，则∠AEC＝____________．

【正确答案】69°．

【详解】试题分析：∠AEC＝180°-∠EAC-∠ECA，因为△ABC的外角∠DAC和∠ACF的平分线交于点E，所以∠EAC=∠DAC，∠ECA=∠ACF，所以∠AEC＝180°-∠DAC-∠ACF=（360°-∠DAC-∠ACF）=（180°-∠DAC+180°-∠ACF）=（∠BAC+∠ACB）=(180°-∠B)=69°.
12. 如图，在△ABC和△FDE中，AD=FC，AB=EF，当添加条件_______时，就可得到△ABC≌△FED．（只需填写一个正确条件即可）

【正确答案】BC=ED或∠A∠F或AB∥EF或∠B=∠E=RT∠等

【分析】要得到△ABC≌△FED，现有条件为两边分别对应相等，找到全等已经具备的条件，根据全等的判定方法选择另一条件即可得等答案．
【详解】∵AD=FC，∴AC=FD，又AB=EF，加BC=DE就可以用SSS判定△ABC≌△FED；
加∠A=∠F或AB∥EF就可以用SAS判定△ABC≌△FED；
加∠B=∠E=90°就可以用HL判定△ABC≌△FED．
故答案为BC=ED或∠A=∠F或AB∥EF或∠B=∠E=90°．
本题考查了三角形全等的判定方法．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA没有能判定两个三角形全等，没有能添加，根据已知图形及判定方法选择条件是正确解答本题的关键．
13. 如图所示，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，若DE＝2，则EC＝_________．

【正确答案】8．

【详解】因为AB=AC，∠BAC=120°，所以∠B=∠C=30°.
因为DE垂直平分AB，所以EA=EB，∠ADE=90°，所以∠B=∠EAB=30°，
所以∠EAC=120°-30°=90°.
Rt△ADE中，AE=2DE=2×2=4.
Rt△CAE中，CE=2AE=2×4=8.
故答案为8.
14. 某种电子元件的面积大约为0.00000069平方毫米，将0.00000069这个数用科学记数法表示为______．
【正确答案】6.9×10﹣7．

【详解】试题分析：对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法没有同的是其所使用的是负指数幂，指数由原数左边起个没有为零的数字前面的0的个数所决定．所以0.00000069=6.9×10﹣7．
考点：科学记数法．
15. 若关于x的方程无解，则m=_____．
【正确答案】－8

【详解】解：∵关于x的方程无解，
∴x=5，
解分式方程，
去分母得：，
将x=5代入得：m=－8.
三、解 答 题：（共90分）
16. （1）计算：5a3b·（－3b）2＋（－ab）（－6ab）2；
（2）先化简（a2b－2ab2－b3）÷b－（a＋b）（a－b），然后对式子中a、b分别选择一个自己最喜欢的数代入求值．
（3）解方程.
【正确答案】（1）9a3b3；（2）－2ab，若取a＝1，b＝－1，则原式＝2；（3）x＝3．

【详解】试题分析：先进行幂的乘方运算，然后进行单项式乘单项式的运算，合并即可．
按照整式的乘法和除法法则进行运算，再合并同类项，选取一对字母的值代入计算即可.
按照解分式方程的步骤解方程即可.
试题解析：（1）原式
（2）原式
如选择一个喜欢的数为，原式
（3）去分母，两边都乘以 得

解得
经检验是原方程的根．
原方程的解是：
17. 已知，求的值．
【正确答案】-5．

【详解】试题分析：已知等式左边通分并利用同分母分式的加法法则变形，代入原式计算即可得到结果．
试题解析：显然xy≠0．将待求式的分子、分母同时除以xy，得
已知等式整理得：，即
则原式
18. 如图是由三个阴影的小正方形组成的图形，请你在三个网格图中，各补画出一个有阴影的小正方形，使补画后的图形为轴对称图形．

【正确答案】答案见解析．

【详解】试题分析：根据轴对称的概念作答，如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．
试题解析：如图所示：

19. 如图所示，求∠A＋∠B＋∠C＋∠D＋∠E．

【正确答案】180°

【详解】试题分析：根据外角的性质得∠1＝∠A＋∠E，∠2＝∠B＋∠C，然后放在一个三角形里，再根据三角形内角和是180°，即可求得∠A＋∠B＋∠C＋∠D＋∠E＝180°
解：∵∠1＝∠A＋∠E，∠2＝∠B＋∠C，
∴∠A＋∠B＋∠C＋∠D＋∠E＝∠1＋∠2＋∠D＝180°

20. 如图所示，若 MP和 NQ 分别垂直平分AB和 AC．
（1）若△APQ的周长为12，求 BC的长；
（2）∠BAC=105°，求∠PAQ 的度数．

【正确答案】（1）12；（2）30°．

【详解】试题分析：
（1）根据线段的垂直平分线的性质证PA=PB，QA=AC.
（2）等腰三角形的性质和三角形的内角和定理求解.
试题解析：
(1)∵MP和NQ分别垂直平分AB和AC，∴AP＝BP，AQ＝CQ.
∴△APQ的周长为AP＋PQ＋AQ＝BP＋PQ＋CQ＝BC.
∵△APQ的周长为12，
∴BC＝12.
(2)∵AP＝BP，AQ＝CQ，
∴∠B＝∠BAP，∠C＝∠CAQ.
∵∠BAC＝105°，
∴∠BAP＋∠CAQ＝∠B＋∠C＝180°－∠BAC＝180°－105°＝75°.
∴∠PAQ＝∠BAC－(∠BAP＋∠CAQ)＝105°－75°＝30°.
21. 有一项工程，若甲队单独做，恰好在规定日期完成，若乙队单独做要超过规定日期3天完成；现在先由甲、乙两队合做2天后，剩下的工程再由乙队单独做，也刚好在规定日期完成，问规定日期多少天？
【正确答案】规定日期是6天．

【分析】本题的等量关系为：甲工作2天完成的工作量+乙规定日期完成的工作量=1，把相应数值代入即可求解．
【详解】解：设工作总量为1，规定日期为x天，则若单独做，甲队需x天，乙队需x+3天，根据题意列方程得

解方程可得x=6，
经检验x=6是分式方程的解．
答：规定日期是6天．


22. 已知：∠AOB=90°,OM是∠AOB平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D. 求证：PC=PD.

【正确答案】见解析

【分析】过P分别作PE⊥OB于E，PF⊥OA于F，由角平分线的性质易得PE＝PF，然后由同角的余角相等证明∠1＝∠2，即可由ASA证明△CFP≌△DEP，从而得证．
【详解】证明：过P分别作PE⊥OB于E，PF⊥OA于F，
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线，
∴PE=PF,
∵∠1+∠FPD=90°
又∵∠AOB=90°
∴∠FPE=90°，
∴∠2+∠FPD=90°
∴∠1=∠2,
∵在△CFP和△DEP中：，
∴△CFP≌△DEP(ASA)
∴PC=PD.

此题主要考查角平分线的性质和全等三角形的判定和性质，难度中等，作辅助线很关键．
23. （1）阅读理解：
如图 1，在△ABC 中，若 AB=10，AC=6，求 BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长 AD到点 E使 DE=AD，连接 BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把 AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线 AD的取值范围是__________.
（2）问题解决：如图2，在△ABC中，D是 BC边上的中点,DE⊥DF 于点 D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．

【正确答案】（1）2