冀教版八年级下册第十九章 平面直角坐标系19.2 平面直角坐标系优秀课件ppt

这是一份冀教版八年级下册第十九章 平面直角坐标系19.2 平面直角坐标系优秀课件ppt，共41页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，探索新知，典题精讲，易错提醒，小试牛刀等内容，欢迎下载使用。

1.什么是平面直角坐标系？2.你能在平面直角坐标系中描出下列各点吗？ A (4，2) B(3，3) C(0，5) D(－3，－3)3.(－5，5)和(5，－5)表示同一个点吗？
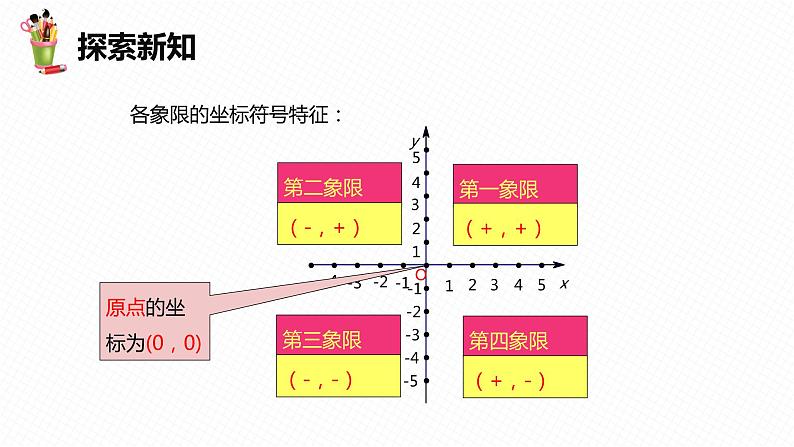
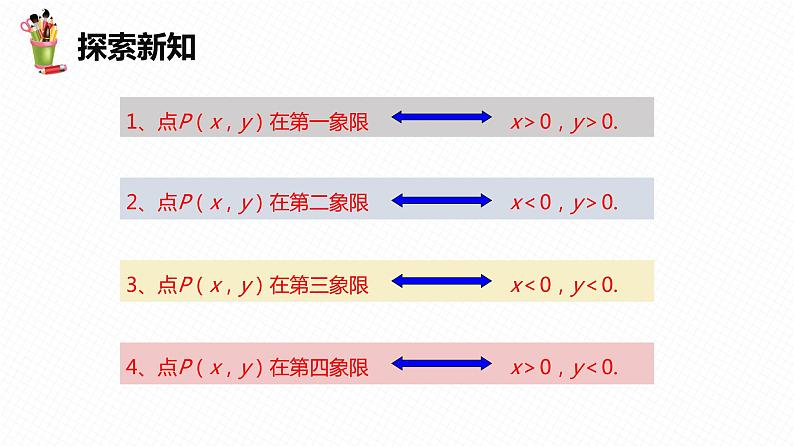
1、直角坐标系的横轴和纵轴将平面分成 ____ 部分， 从右上方的部分说起，按逆时针方向，各部分 依次是__________、 _________ 、 _________ 和__________. 2、坐标轴上的点属于哪一象限？
原点的坐标为(0，0)
各象限的坐标符号特征：
在平面直角坐标系中，点A(2，－3)在第(　　)象限．A．一　　　　　　　 B．二　　　　　　　C．三　　　　　　 　D．四
根据平面直角坐标系中四个象限内的点的坐标特征，即可确定点的位置. 答案：D
由点的坐标确定点的位置的方法：方法一是由点的坐标的符号确定点的位置，即(＋，＋)的点在第一象限，(－，＋)的点在第二象限，(－，－)的点在第三象限，(＋，－)的点在第四象限；方法二是分别过两坐标轴上表示该点的坐标的点作两坐标轴的垂线，这两条垂线的交点位置即为该点的位置．
点A (－3，4)在_______象限，到x 轴的距离为________，到y 轴的距离为______，到原点的距离为_______.
下列说法错误的是(　　)A．象限内的点的坐标可用一个有序数对来表示B．坐标轴上的点的坐标可用一个有序数对来表示C．过点P 向x 轴作垂线，点P 与垂足之间的线段 长是点P 的纵坐标D．过点P 向y 轴作垂线，点P 与垂足之间的线段 长不一定是点P 的横坐标
若点P (a，b)到x 轴的距离为2，到y 轴的距离为1，且在第二象限，则点P 的坐标为(　　)A．(－2，1) B．(1，2)C．(－1，2) D．(－1，－2)
在平面直角坐标系中，若点A(a，－b)在第一象限内，则点B (a，b)所在的象限是(　　)A．第一象限 B．第二象限C．第三象限 D．第四象限
拓展：平行于x 轴的直线上的点的纵坐标相等；平行于y 轴的直线上的点的横坐标相等．
例3 已知点P (x＋6，x－4)在y 轴上，则点P 的坐标是 __________．
导引：根据y 轴上点的坐标的特征可得x＋6＝0，得x＝－6， 所以x－4＝－10.故点P 的坐标是(0，－10)．
下列坐标平面内的各点中，在坐标轴上的是(　　)A．(3，3) B．(－3，0)C．(－1，2) D．(－2，－3)
如果点A (a＋3，a )在y 轴上，那么点A 的坐标是(　　)A．(0，3) B．(0，－3)C．(3，0) D．(－3，0)
已知点P（0，m）在y 轴的负半轴上，则点M（－m，－m＋1）在（　　）A．第一象限 B．第二象限C．第三象限 D．第四象限
关于x 轴、y 轴和原点对称的点的坐标特征
关于x 轴对称的点，横坐标相等，纵坐标互为相反数；关于y 轴对称的点，横坐标互为相反数，纵坐标相等．关于原点对称的点，横坐标和纵坐标都互为相反数．
已知点A (a，－5)，B (8，b)，根据下列要求，确定a，b 的值．(1)A，B 两点关于y 轴对称；(2)A，B 两点关于原点对称；(3)AB∥x 轴；(4)A，B 两点在第一、三象限的角平分线上．
(1)两点关于y 轴对称时，它们的横坐标互为相反数，而纵坐标相同；(2)两点关于原点对称时，两点的横、纵坐标都互为相反数；(3)两点连线平行于x 轴时，这两点纵坐标相同(但横坐标不同)；(4)当两点位于第一、三象限的角平分线上时，每个点的横、纵坐标相同．
(1)当点A (a，－5)，B (8，b)关于y 轴对称时， 有a＝－8，b＝－5.(2)当点A (a，－5)，B (8，b)关于原点对称时， 有a＝－8，b＝5.(3)当AB∥x 轴时，有a≠8，b＝－5.(4)当A，B 两点位于第一、三象限的角平分线 上时，有a＝－5，b＝8.
点B (3，－5)在第_____象限，其关于x 轴的对称点的坐标为________，关于y 轴的对称点的坐标为____________，关于原点的对称点的坐标为 .
在直角坐标系中，点A 的坐标为(4，2).(1)分别画出点A 关于x 轴，y 轴，和原点的对称点 B，C，D. 并分别写出点B，C，D 的坐标.(2)四边形ABDC 是轴对称图形吗？如果是轴对 称图形，请画出它的对称轴.
(1)如图．B (4，－2)， C (－4，2)，D (－4，－2)．(2)是．对称轴l1，l2 如图所示．
点P (2，5)关于x 轴对称的点的坐标为(　　)A．(－2，5) B．(5，2)C．(－2，－5) D．(2，－5)
已知点P 的坐标为(x，y )，且(x＋1)2＋ ＝0，则点P 关于原点的对称点P ′的坐标是(　　)A. B.C. D.
在平面直角坐标系中，点P (－7，3)关于原点的对称点Q 的坐标为(　　)A．(7，－3) B．(7，3)C．(3，－7) D．(－7，－3)点(4，3)与点(－4，3)的关系是(　　)A．关于原点对称 B．关于y 轴对称C．关于x 轴对称 D．不能构成对称关系
若点P (a，b)在第二象限，则点M (b－a，a－b)在(　　)A．第一象限 B．第二象限C．第三象限 D．第四象限
易错点：对直角坐标系内的点的坐标的符号理解不清而致错.
错解：A或B或C诊断：错解产生的原因有两个：一是对各象限内点的坐标特点没有掌握好，二是没有弄清b－a与a－b的符号．正解：D解题策略：根据各象限内的点的坐标的符号特点，先判定a 与b 的符号，再确定b－a 与a－b 的符号．
如图为A，B，C 三点在坐标平面上的位置图．若A，B，C 的x坐标的数字总和为a，y 坐标的数字总和为b，则a－b 之值为何？（　　）A．5 　　　　B．3 C．－3 　　　　D．－5
点M (a，b)为平面直角坐标系中的点．(1)当a>0，b<0时，点M 位于第几象限？(2)当ab>0时，点M 位于第几象限？(3)当a 为任意非零实数，且b<0时，点M 位于第几象限？
(1)第四象限．(2)因为ab＞0，所以a＞0且b＞0或a＜0且b＜0. 所以点M 位于第一象限或第三象限．(3)第三象限或第四象限.
如图，给出格点三角形ABC.(1)写出三角形ABC 各顶点的坐标；(2)求出此三角形的面积．
(1)A (2，2)，B (－2，－1)，C (3，－2)．(2)S三角形ABC＝4×5－ ×3×4－ ×1×4－ ×1×5 ＝9.5.
如图所示．(1)请写出A，B，C，D，E 五点的坐标．
(1)A (2，4)，B (－1，2)， C (－1，－1)， D (1，－4)，E (4，－4)．
(2)通过观察B，C 两点的坐标，你发现了什么？线段BC 的位置有什么特点？由此你得出什么结论？通过进一步观察D，E 两点的坐标你发现了什么？线段DE 的位置有什么特点？由此你又能得出什么结论？
(2)通过观察B，C 两点的坐标，发现B，C 两点的横坐标相同，纵坐标不同．线段BC 与y 轴平行，与x 轴垂直．由此可得出若一条直线上的所有点的横坐标均相同，纵坐标不同，则此直线与y 轴平行(或就是y 轴)，也可以说与x 轴垂直．通过观察D，E 两点的坐标，发现D，E 两点的纵坐标相同，横坐标不同．线段DE 与x 轴平行，与y 轴垂直．由此可得出若一条直线上的所有点的纵坐标均相同，横坐标不同，则此直线与x 轴平行(或就是x 轴)，也可以说与y 轴垂直．
在平面直角坐标系中，一只蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位长度．其行走路线如图所示．(1)填写下列各点的坐标： A1(___，___)，A3(___，___)，A12(____，___)；
(2)写出点A4n 的坐标(n 是正整数)；
(2)当n＝1时，点A4 的坐标是(2，0)， 当n＝2时，点A8 的坐标是(4，0)， 当n＝3时，点A12 的坐标是(6，0)， … 所以点A4n 的坐标是(2n，0)．
(3)指出蚂蚁从点A100 到点A101 的移动方向．
(3)100正好是4的倍数， 所以点A100 和A101 的坐标分别是A100 (50，0)， A101 (50，1)， 所以蚂蚁从点A100 到点A101 的移动方向是向上．
1. 第一、二、三、四象限内点的坐标的符号依次 为(＋，＋)，(－，＋)，(－，－)，(＋，－)．2．x 轴上的点纵坐标为0，y 轴上的点横坐标为0.
3．纵坐标相同的点的连线平行于x 轴(或与x 轴重合)； 横坐标相同的点的连线平行于y 轴(或与y 轴重合)．4．关于x 轴对称的点横坐标相等，纵坐标互为相反数； 关于y 轴对称的点横坐标互为相反数，纵坐标相等； 关于原点对称的点横、纵坐标都互为相反数.