




初中数学中考复习 专题12几何模型-将军饮马模型(将军饮马、将军遛马、造桥选址等)-2022年中考数学第二轮总复习课件(全国通用)
展开“线段最值”问题是中考的热点问题(每年必考),题型多样,变化灵活,综合性强,考查的知识点众多,涉及多种数学思想、方法和技能技巧,对学生的各种能力要求较高,一般都是各题型的压轴题,拉分题. 深刻理解把握这一问题的基本原理、解决策略,利于我们把握中考方向,在教学实践中才能做到有的放矢,提高教学的针对性、有效性.
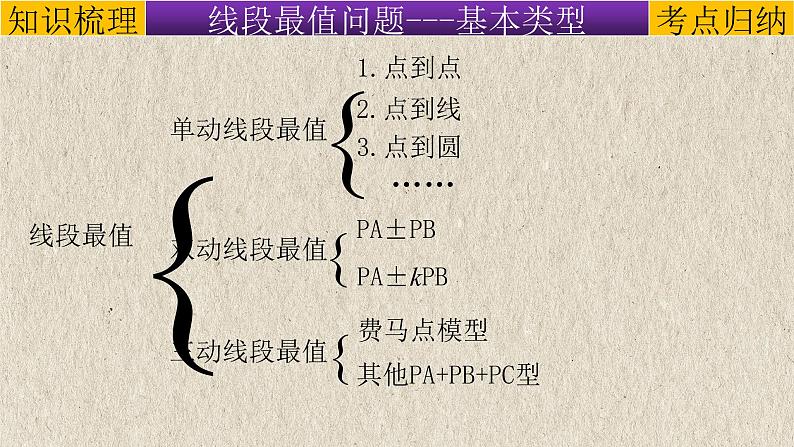
其他PA+PB+PC型
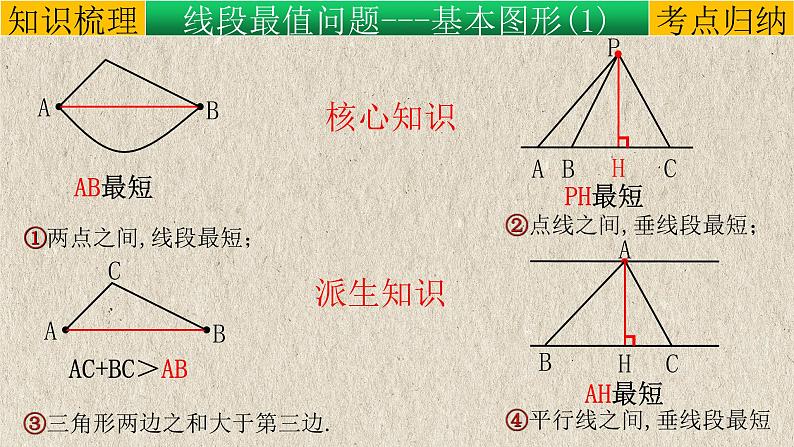
①两点之间,线段最短;
③三角形两边之和大于第三边.
②点线之间,垂线段最短;
④平行线之间,垂线段最短
复杂的几何最值问题都是在基本图形的基础上进行变式得到的,在解决这一类问题的时候,常常需要通过几何变换进行转化,逐渐转化为“基本图形”,再运用“基本图形”的知识解决.常运用的典型几何变换有: (1)翻折---将军饮马; (2)平移---造桥选址; (3)旋转---费马点问题; (4)相似---阿氏圆问题; (5)三角---胡不归问题; (6)多变换综合运用。
1.分析定点、动点,寻找不变特征; 2.确定路径(关键):通过起点、终点、特殊点猜测运动路径(轨迹), 并结合不变特征进行验证; 3.①若属于常见模型,调用模型解决问题; ②若不属于常见模型,要结合所求目标, 根据不变特征转化为基本定理或函数解决问题. 4.设计方案,求出路径长.
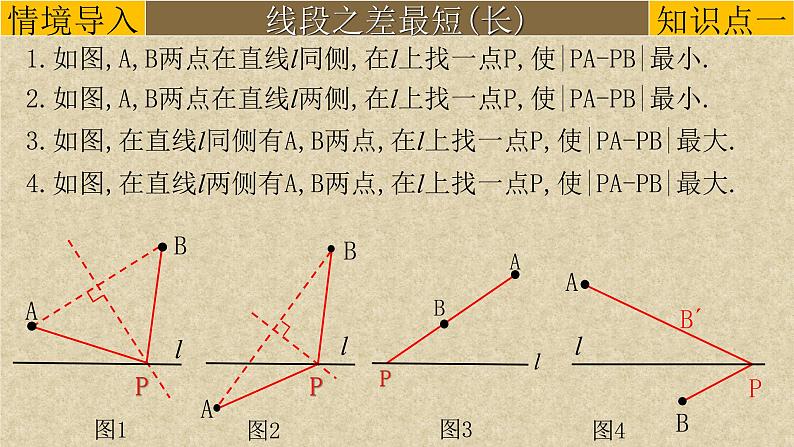
1.如图,A,B两点在直线l同侧,在l上找一点P,使|PA-PB|最小.
4.如图,在直线l两侧有A,B两点,在l上找一点P,使|PA-PB|最大.
2.如图,A,B两点在直线l两侧,在l上找一点P,使|PA-PB|最小.
3.如图,在直线l同侧有A,B两点,在l上找一点P,使|PA-PB|最大.
【例1】如图,已知二次函数y=x2+4x-5的图象及对称轴,请用无刻度直尺按下列要求作图.(1)在图1中作点P(-4,-5);(2)已知点P(-4,-5),在图2中的对称轴上作一点Q,使QC-QA的值最大.
利用将军饮马求线的和的最值问题
利用轴对称或梯形四点共线作图
【引例】如图,一位将军骑马从驻地A出发,先牵马去河边MN喝水,再回到驻地B.这位将军怎样走路程最短?
将军沿A-P-B走路程最短.
图形特征: 适用模型:基本策略:基本方法:基本原理:解题关键:
同侧化异侧、折线化直线;
N个动点N条河,N次对称跑不脱;
图形特征:两定一动;适用模型:将军饮马;基本策略:同侧化异侧、折线化直线;基本方法:N个动点N条河,N次对称跑不脱;基本原理:两点之间线段最短;解题关键:根据结论抓点、线.
PA+PB=_______.
PA+PB=_______=____.
【引例1】如图,A,B均为驻地,将军某一天要从驻地A出马,先到草地边某处牧马,再到河边饮马,然后回到驻地B,这位怎样走路程最短?
将军沿A-C-D-B走路程最短
图形特征:两定两动;适用模型:将军遛马(台球两次碰壁);基本策略:同侧化异侧、折线化直线;基本方法:N个动点N条河,N次对称跑不脱;基本原理:两点之间线段最短;解题关键:根据结论抓点、线.
【引例2】如图,一位将军骑马从驻地A出发,先牵马去草地OM吃草,再牵马去河边ON喝水,最后回到驻地A.这位怎样走路程最短?
将军沿A-B-C-A走路程最短
图形特征:两定两动;适用模型:将军遛马;基本策略:同侧化异侧、折线化直线;基本方法:N个动点N条河,N次对称跑不脱;基本原理:两点之间线段最短;解题关键:根据结论抓点、线.
【例3-1】如图,点A(a,3)B(b,1)都在双曲线 上,点C,D分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( ) A. B. C. D.
1.(1)如图①,在AB直线一侧C,D两点,在AB上找一点P,使C,D,P三点组成的三角形的周长最短,找出此点并说明理由.(2)如图②,在∠AOB内部有一点P,是否在OA,OB上分别存在点E,F,使得E,F,P三点组成的三角形的周长最短,并说明理由.(3)如图③,在∠AOB内部有两点M,N,是否在OA,OB上分别存在点E,F,使得E,F,M,N,四点组成的四边形的周长最短,并说明理由.
2.如图,抛物线y=0.5x²-4x+4与y轴交于点A,点B是OA的中点.一个动点G从点B出发,先经过x轴上的点M,再经过抛物线对称轴上的点N,然后返回到点A.如果动点G走过的路程最短为____,则点M、N的坐标为________________,
M(8/3,0)N(4,1)
【引例】“变态的将军饮马”--- 造桥选址问题 将军每日需骑马从军营A出发,去河对岸的瞭望台B观测敌情,已知河流的宽度为30米,请问,在何地修浮桥,使每日的行程最短?
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?
我们能否在不改变AM+MN+BN的前提下把桥转化到一侧呢?什么图形变换能帮助我们?
图形特征:两定两动;适用模型:造桥选址;基本方法:将一定点沿定长方向平移定长距离, 再用将军饮马模型解决问题;基本原理:两点之间线段最短;解题关键:根据结论抓点、线.
如图,荆州古城河在CC´处直角转弯,河宽相同,从A处到B处,须经两座桥:DD´,EE´(桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD´E´EB的路程最短?
【例4-1】如图,菱形ABCD中,AB=4,∠BAD=60º,M,N是AC上两动点,且MN=2,则BM+BN的最小值为_____.
【例4-2】在矩形ABCD,AB=6,BC=8,G为AD的中点.如图,E,F为边AB上的两个动点,且EF=4,当四边形CGEF的周长最小时,则AF=___.
1.已知A(1,1),B(4,2),(1)点P为x轴上一动点,求|PA-PB|的值最大时P点的坐标;(2)点P为x轴上一动点,求PA+PB的最小值和此时P点的坐标;(3)CD为x轴上一条动线段,且CD=1,求AC+CD+DB的最小值和此时C点的坐标.
PA+PB的最小值为 ,
AC+CD+DB的最小值为 ,
【例5】如图,在Rt△ABC中∠ACB=90º,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为_____.
图形特征: 基本策略:基本原理:解题关键:
1.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为____.2.如图,∠BAC=30º,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为____.
将军饮马:这个将军饮的不是马,是数学!解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称.解题策略:对称、翻折→化同为异;化异为同;化折为直.口 诀:和与差,求最值,将军饮马七模型!
两村一路(异侧)和最小
两村一路(同侧)差最大
两村一路(异侧)差最大
两村一路(同侧)和最小
(经典版)中考数学二轮复习课件:专题12几何模型-将军饮马模型(将军饮马、将军遛马、造桥选址等) (含解析): 这是一份(经典版)中考数学二轮复习课件:专题12几何模型-将军饮马模型(将军饮马、将军遛马、造桥选址等) (含解析),共33页。PPT课件主要包含了线段最值,单动线段最值,双动线段最值,三动线段最值,点到点,点到线,点到圆,PA±PB,PA±kPB,费马点模型等内容,欢迎下载使用。
”将军饮马“模型课件-数学中考复习: 这是一份”将军饮马“模型课件-数学中考复习,共26页。PPT课件主要包含了模型一两定一动,数学建模思想,模型二两动一定,模型三两定两动,“将军饮马”模型,解题方法,运用新知,课堂小结等内容,欢迎下载使用。
2023年中考数学二轮复习必会几何模型剖析--2.1 “将军饮马”模型(将军饮马、将军遛马、将军造桥)(轴对称模型)(精品课件): 这是一份2023年中考数学二轮复习必会几何模型剖析--2.1 “将军饮马”模型(将军饮马、将军遛马、将军造桥)(轴对称模型)(精品课件),共22页。PPT课件主要包含了线段最值,单动线段最值,双动线段最值,三动线段最值,点到点,点到线,点到圆,PA±PB,PA±kPB,费马点模型等内容,欢迎下载使用。












