2023 鲁教版（五四制）数学八年级下册开学测试卷（二）

这是一份2023 鲁教版（五四制）数学八年级下册开学测试卷（二），文件包含2023鲁教版五四制数学八年级下册开学测试卷二解析版docx、2023鲁教版五四制数学八年级下册开学测试卷二原卷版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
开学测试卷二
一．选择题（共12小题，满分36分，每小题3分）
1．（3分）因式分解：1﹣4y2＝（　　）
A．（1﹣2y）（1+2y） B．（2﹣y）（2+y）
C．（1﹣2y）（2+y） D．（2﹣y）（1+2y）
2．（3分）如图，Rt△ABC中，∠C＝90°，BC＝3，AC＝4，将△ABC绕点B逆时针旋转得△A′BC'，若点C′在AB上，则AA′的长为（　　）

A． B．4 C．2 D．5
3．（3分）若分式的值为0，则x的值为（　　）
A．3或﹣2 B．3 C．﹣2 D．﹣3或2
4．（3分）如果x2﹣（m﹣1）x+1是一个完全平方式，则m的值为（　　）
A．﹣1 B．1 C．﹣1或3 D．1或3
5．（3分）如图，在平行四边形ABCD中，DE平分∠ADC交BC边于点E，已知BE＝4cm，AB＝6cm，则AD的长度是（　　）

A．4cm B．6cm C．8cm D．10cm
6．（3分）某班数学兴趣小组10名同学的年龄情况如下表：
年龄（岁）
12
13
14
15
人数
1
4
4
1
则这10名同学年龄的平均数和中位数分别是（　　）
A．13.5，13.5 B．13.5，13 C．13，13.5 D．13，14
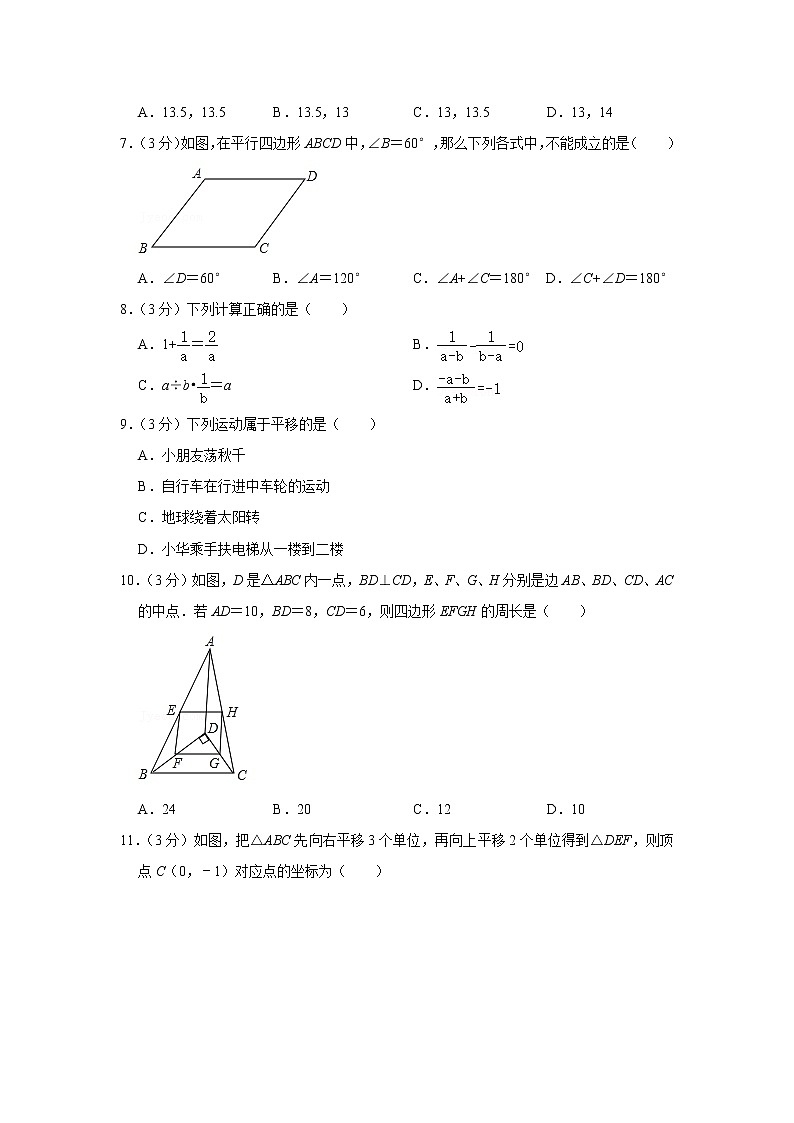
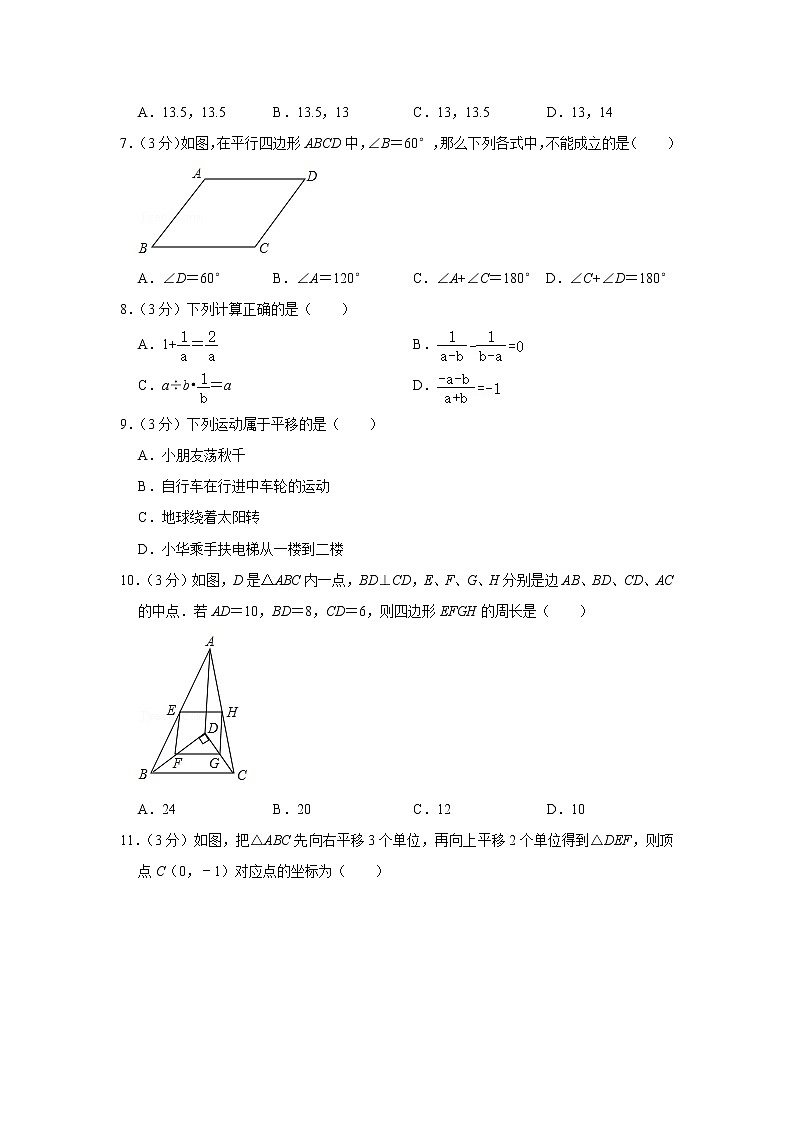
7．（3分）如图，在平行四边形ABCD中，∠B＝60°，那么下列各式中，不能成立的是（　　）

A．∠D＝60° B．∠A＝120° C．∠A+∠C＝180° D．∠C+∠D＝180°
8．（3分）下列计算正确的是（　　）
A．1+＝ B．
C．a÷b•＝a D．
9．（3分）下列运动属于平移的是（　　）
A．小朋友荡秋千
B．自行车在行进中车轮的运动
C．地球绕着太阳转
D．小华乘手扶电梯从一楼到二楼
10．（3分）如图，D是△ABC内一点，BD⊥CD，E、F、G、H分别是边AB、BD、CD、AC的中点．若AD＝10，BD＝8，CD＝6，则四边形EFGH的周长是（　　）

A．24 B．20 C．12 D．10
11．（3分）如图，把△ABC先向右平移3个单位，再向上平移2个单位得到△DEF，则顶点C（0，﹣1）对应点的坐标为（　　）

A．（0，0） B．（1，2） C．（1，3） D．（3，1）
12．（3分）已知x2﹣3x﹣1＝0，x≠0，那么x2+＝（　　）
A．9 B．10 C．11 D．12
二．填空题（共6小题，满分18分，每小题3分）
13．（3分）如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B＝90°，AB＝10，DH＝4，平移距离为7，求阴影部分的面积为　 　．

14．（3分）已知a＝7﹣3b，则代数式a2+6ab+9b2的值为 　 　．
15．（3分）如图是用平行四边形纸条沿对边AB，CD上的点E，F所在的直线折成的V字形图案，已知图中∠2＝64°，则∠1的度数是　 　．

16．（3分）已知一组数据0，2，x，4，5的众数为4，那么这组数据方差是　 　．
17．（3分）如图，六边形ABCDEF的各角都相等，若m∥n，则∠1+∠2＝　 　°．

18．（3分）若关于x的分式方程＝1的解为负数，则m的取值范围为 　 　．
三．解答题（共7小题，满分66分）
19．（7分）化简：．20．（7分）因式分解：（y2﹣y）2﹣14（y2﹣y）+24．
21．（8分）如图，在平行四边形ABCD中，E、F分别是CD，AB上的点，且DE＝BF，求证：
（1）CE＝AF；
（2）四边形AFCE是平行四边形．

22．（8分）京东快递仓库使用机器人分拣货物，已知一台机器人的工作效率相当于一名分拣工人工作效率的20倍，若用一台机器人分拣8000件货物，比原先16名工人分拣这些货物要少用小时．
（1）求一台机器人一小时可分拣多少件货物？
（2）受“双十一”影响，石家庄某京东仓库11月11日当天收到快递72万件，为了在8小时之内分拣完所有快递货物，公司调配了20台机器人和20名分拣工人，工作3小时之后，又调配了15台机器人进行增援，该公司能否在规定的时间内完成任务？请说明理由．
23．（11分）计算公式：设一组数据含有n个数x1，x2，…，xn．
（1）写出这组数据的平均数的计算公式；
（2）设f1，f2，…，fn是一组权数，用数学式子表示权数应具备的两个性质；
（3）写出x1，x2，…，xn以f1，f2，…，fn为权的加权平均数的计算公式；
（4）用M，m分别表示这组数据的最大值和最小值，写出求这组数据的极差的计算公式；
（5）写出求这组数据的方差的计算公式．
24．（12分）如图，在四边形ABCD中，对角线AC和BD相交于点E，且DA＝DB＝DC．
（1）求证：∠ADB＝2∠ACB；
（2）如图2，点F在BC边上，AC与DF相交于点G，DE＝BF，若∠BAC＝30°，5CG＝3DG，试探究AG与DG的数量关系，并说明理由；
（3）如图3，在（2）的条件下，BN与DF相交于点M，若2∠BNC﹣2∠BFD＝∠BCE，BC＝7，求线段DM的长．

25．（13分）（1）【操作发现】
如图1，将△ABC绕点A顺时针旋转50°，得到△ADE，连接BD，则∠ABD＝　 　度．

（2）【解决问题】
①如图2，在边长为的等边三角形ABC内有一点P，∠APC＝90°，∠BPC＝120°，求△APC的面积．
②如图3，在△ABC中，∠ACB＝90°，AC＝BC，P是△ABC内的一点，若PB＝1，PA＝3，∠BPC＝135°，则PC＝　 　．
（3）【拓展应用】
如图4是A，B，C三个村子位置的平面图，经测量AB＝4，BC＝3，∠ABC＝75°，P为△ABC内的一个动点，连接PA，PB，PC．求PA+PB+PC的最小值．

开学测试卷二
参考答案与试题解析
一．选择题（共12小题，满分36分，每小题3分）
1．（3分）因式分解：1﹣4y2＝（　　）
A．（1﹣2y）（1+2y） B．（2﹣y）（2+y）
C．（1﹣2y）（2+y） D．（2﹣y）（1+2y）
【分析】直接利用平方差公式分解因式得出答案．
【解答】解：1﹣4y2
＝1﹣（2y）2
＝（1﹣2y）（1+2y）．
故选：A．
【点评】此题主要考查了公式法分解因式，正确应用乘法公式是解题关键．
2．（3分）如图，Rt△ABC中，∠C＝90°，BC＝3，AC＝4，将△ABC绕点B逆时针旋转得△A′BC'，若点C′在AB上，则AA′的长为（　　）

A． B．4 C．2 D．5
【分析】连接AA'，由旋转的性质得出AC'、A'C'的长度，利用勾股定理即可得出答案．
【解答】解：如图，连接AA'，

∵将△ABC绕点B逆时针旋转得△A′BC'，
∴∠A'C'B＝∠C＝90°，A'C'＝AC＝4，AB＝A'B，
根据勾股定理得：
AB＝＝5，
∴A'B＝AB＝5，
∴AC'＝AB﹣BC'＝2，
在Rt△AA'C'中，由勾股定理得：
AA'＝＝2，
故选：C．
【点评】本题主要考查了旋转的性质，勾股定理等知识，熟练掌握旋转的性质是解题的关键．
3．（3分）若分式的值为0，则x的值为（　　）
A．3或﹣2 B．3 C．﹣2 D．﹣3或2
【分析】分式的值是0的条件是：分子为0，分母不为0．
【解答】解：∵x2﹣x﹣6＝0，
∴x＝3或﹣2，
当x＝3时，x2﹣3x+2≠0，∴x＝3值是0．
当x＝﹣2时，x2﹣3x+2≠0，∴当x＝﹣2时分式的值是0．
∴x＝3或﹣2．
故选：A．
【点评】分式是0的条件中特别需要注意的是分母不能是0，这是经常考查的知识点．
4．（3分）如果x2﹣（m﹣1）x+1是一个完全平方式，则m的值为（　　）
A．﹣1 B．1 C．﹣1或3 D．1或3
【分析】利用完全平方公式的结构特征判断即可确定出m的值．
【解答】解：∵x2﹣（m﹣1）x+1是一个完全平方式，
∴m﹣1＝±2，
解得：m＝﹣1或3，
故选：C．
【点评】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．
5．（3分）如图，在平行四边形ABCD中，DE平分∠ADC交BC边于点E，已知BE＝4cm，AB＝6cm，则AD的长度是（　　）

A．4cm B．6cm C．8cm D．10cm
【分析】由已知平行四边形ABCD，DE平分∠ADC可推出△DCE为等腰三角形，所以得CE＝CD＝AB＝6，那么AD＝BC＝BE+CE，从而求出AD．
【解答】解：已知平行四边形ABCD，DE平分∠ADC，
∴AD∥BC，CD＝AB＝6，∠EDC＝∠ADE，AD＝BC，
∴∠DEC＝∠ADE，
∴∠DEC＝∠CDE，
∴CE＝CD＝6，
∴BC＝BE+CE＝4+6＝10，
∴AD＝BC＝10，
故选：D．
【点评】此题考查的知识点是平行四边形的性质及角平分线的性质，关键是由平行四边形的性质及角平分线的性质得等腰三角形通过等量代换求出AD．
6．（3分）某班数学兴趣小组10名同学的年龄情况如下表：
年龄（岁）
12
13
14
15
人数
1
4
4
1
则这10名同学年龄的平均数和中位数分别是（　　）
A．13.5，13.5 B．13.5，13 C．13，13.5 D．13，14
【分析】根据加权平均数和中位数的定义列式计算即可．
【解答】解：这10位同学年龄的平均数为＝13.5，
中位数为＝13.5，
故选：A．
【点评】本题主要考查加权平均数和中位数，熟练掌握加权平均数和中位数的定义是解题的关键．
7．（3分）如图，在平行四边形ABCD中，∠B＝60°，那么下列各式中，不能成立的是（　　）

A．∠D＝60° B．∠A＝120° C．∠A+∠C＝180° D．∠C+∠D＝180°
【分析】由于平行四边形中相邻内角互补，对角相等，而∠A和∠C是对角，而它们和∠B是邻角，∠D和∠B是对角，由此可以分别求出它们的度数，问题得解．
【解答】解：∵四边形ABCD是平行四边形，
∴∠A＝∠C，∠B＝∠D，
∵∠B＝60°，∠C+∠D＝180°，
∴∠A＝∠C＝120°，∠D＝60°，
∴∠A+∠C＝240°≠180°，
所以C选项是错误的．
故选：C．
【点评】本题考查了平行四边形的性质，熟练掌握平行四边形的性质是解题的关键．
8．（3分）下列计算正确的是（　　）
A．1+＝ B．
C．a÷b•＝a D．
【分析】根据分式的运算法则即可求出答案．
【解答】解：（A）原式＝，故A错误．
（B）原式＝+＝，故B错误．
（C）原式＝aו＝，故C错误．
故选：D．
【点评】本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
9．（3分）下列运动属于平移的是（　　）
A．小朋友荡秋千
B．自行车在行进中车轮的运动
C．地球绕着太阳转
D．小华乘手扶电梯从一楼到二楼
【分析】在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，简称平移．根据平移的概念进而得出答案．
【解答】解：A、小朋友荡秋千，属于旋转变换，此选项错误；
B、行驶的自行车的车轮，属于旋转变换，此选项错误；
C、地球绕着太阳转，属于旋转变换，此选项错误；
D、小华乘手扶电梯从一楼到二楼，属于平移变换，此选项正确；
故选：D．
【点评】此题主要考查了生活中的平移，正确掌握平移的概念是解题关键．
10．（3分）如图，D是△ABC内一点，BD⊥CD，E、F、G、H分别是边AB、BD、CD、AC的中点．若AD＝10，BD＝8，CD＝6，则四边形EFGH的周长是（　　）

A．24 B．20 C．12 D．10
【分析】利用勾股定理列式求出BC的长，再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH＝FG＝BC，EF＝GH＝AD，然后代入数据进行计算即可得解．
【解答】解：∵BD⊥CD，BD＝8，CD＝6，
∴BC＝＝＝10，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴EH＝FG＝BC，EF＝GH＝AD，
∴四边形EFGH的周长＝EH+GH+FG+EF＝AD+BC，
又∵AD＝10，
∴四边形EFGH的周长＝10+10＝20，
故选：B．
【点评】本题考查了三角形的中位线定理，勾股定理的应用，熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键．
11．（3分）如图，把△ABC先向右平移3个单位，再向上平移2个单位得到△DEF，则顶点C（0，﹣1）对应点的坐标为（　　）

A．（0，0） B．（1，2） C．（1，3） D．（3，1）
【分析】利用平移规律进而得出答案．
【解答】解：∵把△ABC先向右平移3个单位，再向上平移2个单位得到△DEF，顶点C（0，﹣1），
∴F（0+3，﹣1+2），
即F（3，1），
故选：D．
【点评】此题主要考查了坐标与图形变化﹣平移，正确得出对应点位置是解题关键．
12．（3分）已知x2﹣3x﹣1＝0，x≠0，那么x2+＝（　　）
A．9 B．10 C．11 D．12
【分析】由x≠0，可将方程两边都除以x得出x﹣＝3，再两边平方，继而得出答案．
【解答】解：∵x2﹣3x﹣1＝0，且x≠0，
∴x﹣3﹣＝0，即x﹣＝3，
∴（x﹣）2＝9，即x2﹣2+＝9，
∴x2+＝11，
故选：C．
【点评】本题主要考查分式的化简求值，解题的关键是掌握等式的基本性质和完全平方公式．
二．填空题（共6小题，满分18分，每小题3分）
13．（3分）如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B＝90°，AB＝10，DH＝4，平移距离为7，求阴影部分的面积为　56　．

【分析】由S△ABC＝S△DEF，推出S四边形ABEH＝S阴即可解决问题．
【解答】解：∵平移距离为7，
∴BE＝7，
∵AB＝10，DH＝4，
∴EH＝10﹣4＝6，
∵S△ABC＝S△DEF，
∴S四边形ABEH＝S阴，
∴阴影部分的面积为＝×（10+6）×7＝56，
故答案为56．

【点评】此题主要考查了平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，要熟练掌握．
14．（3分）已知a＝7﹣3b，则代数式a2+6ab+9b2的值为 　49　．
【分析】先根据完全平方公式变形，再代入，即可求出答案．
【解答】解：∵a＝7﹣3b，
∴a+3b＝7，
∴a2+6ab+9b2
＝（a+3b）2
＝72
＝49，
故答案为：49．
【点评】本题考查了完全平方公式，能熟记完全平方公式是解此题的关键，注意：（a+b）2＝a2+2ab+b2．
15．（3分）如图是用平行四边形纸条沿对边AB，CD上的点E，F所在的直线折成的V字形图案，已知图中∠2＝64°，则∠1的度数是　58o　．

【分析】首先将此题没折叠前的图形补充完整，根据折叠的性质可得∠1＝∠3；又因为平角的定义，可得∠1+∠2+∠3＝180°，可得∠1的度数．
【解答】解：如图所示：根据题意可得：∠3＝∠1，
∵∠1+∠2+∠3＝180°，∠2＝64°，
∴∠1＝（180°﹣64°）÷2＝58°．．
故答案为：58°．

【点评】此题考查了折叠问题，这是中考中的常见题目．解题的关键是掌握折叠前后的图形全等，即对应角与对应边相等．解此题的关键是将折叠前的图形补充完整．
16．（3分）已知一组数据0，2，x，4，5的众数为4，那么这组数据方差是　3.2　．
【分析】先根据众数的定义求出x的值，再求出平均数，继而根据方差公式计算可得．
【解答】解：∵0，2，x，4，5的众数是4，
∴x＝4，
∴这组数据的平均数是（0+2+4+4+5）÷5＝3，
则方差为×[（0﹣3）2+（2﹣3）2+（4﹣3）2+（4﹣3）2+（5﹣3）2]＝3.2，
故答案为：3.2．
【点评】本题主要考查方差，根据众数定义求得x的值，掌握方差的计算公式是解题的关键．
17．（3分）如图，六边形ABCDEF的各角都相等，若m∥n，则∠1+∠2＝　180　°．

【分析】根据六边形ABCDEF的各角都相等，可得六边形ABCDEF的对边平行；延长DC，交直线n于点G，再根据平行线的性质解答即可．
【解答】解：连接DF，延长DC，交直线n于点G，

∵六边形ABCDEF是正六边形，
∴每个内角为：（6﹣2）×180°÷6＝120°，
∴∠E+∠EDC+∠EFA＝360°，
∵∠E+∠EDF+∠EFD＝180°，
∴∠FDC+∠DFC＝180°，
∴AF∥DC，
∴∠2＝∠3，
又∵m∥n，
∴∠3+∠4＝180°，
∵∠4＝∠1，
∴∠1+∠2＝180°，
故答案为：180．
【点评】本题考查了多边形的内角与外角以及平行线的判定与性质，得出AF∥DC是本题的关键．
18．（3分）若关于x的分式方程＝1的解为负数，则m的取值范围为 　m＞1且m≠3　．
【分析】先解关于x的分式方程＝1，得x＝1﹣m．再根据关于x的分式方程＝1的解为负数，得1﹣m＜0且1﹣m≠﹣2，故m＞1且m≠3．
【解答】解：＝1
去分母，得3﹣m＝x+2．
移项，得x＝1﹣m．
∵关于x的分式方程＝1的解为负数，
∴1﹣m＜0且1﹣m≠﹣2．
∴m＞1且m≠3．
故答案为：m＞1且m≠3．
【点评】本题主要考查解分式方程以及解一元一次不等式，熟练掌握解分式方程以及解一元一次不等式是解决本题的关键．
三．解答题（共7小题，满分66分）
19．（7分）化简：．
【分析】根据分式的减法和除法可以解答本题．
【解答】解：
＝[]
＝[﹣]
＝
＝
＝
＝．
【点评】本题考查分式的混合运算，解答本题的关键是明确分式混合运算的计算方法．
20．（7分）因式分解：（y2﹣y）2﹣14（y2﹣y）+24．
【分析】直接利用十字相乘法分解因式得出答案
【解答】解：原式＝（y2﹣y﹣2）（y2﹣y﹣12）
＝（y﹣2）（y+1）（y﹣4）（y+3）．
【点评】此题主要考查了十字相乘法分解因式，正确分解常数项是解题关键．
21．（8分）如图，在平行四边形ABCD中，E、F分别是CD，AB上的点，且DE＝BF，求证：
（1）CE＝AF；
（2）四边形AFCE是平行四边形．

【分析】（1）根据平行四边形的对边相等得AB＝CD，已知DE＝BF，再作线段的差可得CE＝AF；
（2）利用CE与AF平行且相等，可证四边形AFCE是平行四边形．
【解答】证明：（1）∵四边形ABCD为平行四边形，
∴AB＝CD．
又∵DE＝BF，
∴AB﹣BF＝CD﹣DE．
即AF＝CE．
（2）∵AF＝CE，AF∥CE，
∴四边形AFCE是平行四边形．
【点评】本题考查了平行四边形的性质及判定方法．平行四边形的五种判定方法与平行四边形的性质相呼应，每种方法都对应着一种性质，在应用时应注意它们的区别与联系．
22．（8分）京东快递仓库使用机器人分拣货物，已知一台机器人的工作效率相当于一名分拣工人工作效率的20倍，若用一台机器人分拣8000件货物，比原先16名工人分拣这些货物要少用小时．
（1）求一台机器人一小时可分拣多少件货物？
（2）受“双十一”影响，石家庄某京东仓库11月11日当天收到快递72万件，为了在8小时之内分拣完所有快递货物，公司调配了20台机器人和20名分拣工人，工作3小时之后，又调配了15台机器人进行增援，该公司能否在规定的时间内完成任务？请说明理由．
【分析】（1）设一名工人每小时可分拣x件货物，则一台机器人每小时可分拣20x件货物，对于8000件的工作量，时间相差小时，即可列出以时间为等量关系的方程；
（2）根据20台机器人和20名分拣工人3小时分拣的数量+35台机器人和20名分拣工人5小时分拣的数量与72万件比较即可．
【解答】解：（1）设一名工人每小时可分拣x件货物，则一台机器人每小时可分拣20x件货物，
根据题意得：﹣＝，
解得：x＝150，
经检验：x＝150 是原方程的根，
∴20x＝3000，
答：一台机器人每小时可以分拣3000件货物；
（2）该公司能在规定的时间内完成任务，理由：
3×（20×150+20×3000）+（8﹣3）×（35×3000+20×150）＝189000+540000＝729000＞720000，
∴该公司能在规定的时间内完成任务．
【点评】本题考查的是分式方程的应用，明确等量关系进行列式是解题的关键．
23．（11分）计算公式：设一组数据含有n个数x1，x2，…，xn．
（1）写出这组数据的平均数的计算公式；
（2）设f1，f2，…，fn是一组权数，用数学式子表示权数应具备的两个性质；
（3）写出x1，x2，…，xn以f1，f2，…，fn为权的加权平均数的计算公式；
（4）用M，m分别表示这组数据的最大值和最小值，写出求这组数据的极差的计算公式；
（5）写出求这组数据的方差的计算公式．
【分析】（1）根据平均数的定义直接解答即可．
（2）直接根据加权平均数的定义解答即可．
（3）根据加权平均数的定义解答即可．
（4）根据极差的定义直接解答即可．
（5）根据方差的定义直接解答即可．
【解答】解：（1）这组数据的平均数的计算公式为＝（x1+x2+…+xn）；
（2）权的表现形式，一种是比的形式，如4：3：2，另一种是百分比的形式，如创新占50%，综合知识占30%，语言占20%，权的大小直接影响结果；
（3）x1，x2，…，xn以f1，f2，…，fn为权的加权平均数的计算公式为＝；
（4）用M，m分别表示这组数据的最大值和最小值，求这组数据的极差的计算公式为M﹣n；
（5）求这组数据的方差的计算公式为s2＝[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]．
【点评】本题主要考查方差、极差、算术平均数、加权平均数的定义，熟练掌握定义是解答本题的关键．
24．（12分）如图，在四边形ABCD中，对角线AC和BD相交于点E，且DA＝DB＝DC．
（1）求证：∠ADB＝2∠ACB；
（2）如图2，点F在BC边上，AC与DF相交于点G，DE＝BF，若∠BAC＝30°，5CG＝3DG，试探究AG与DG的数量关系，并说明理由；
（3）如图3，在（2）的条件下，BN与DF相交于点M，若2∠BNC﹣2∠BFD＝∠BCE，BC＝7，求线段DM的长．

【分析】（1）由等腰三角形的性质和三角形内角和定理可求解；
（2）由“SAS”可证△CDE≌△DBF，可得∠BDF＝∠DCE，由“SAS”可证△DAQ≌△DCG，可得DQ＝QG＝5a，即可求解；
（3）设∠BCE＝β，由2∠BNC﹣2∠BFD＝∠BCE，可得∠DBN＝β，作BK∥DQ交DF于点K，作BL平分∠DBK交DF于点L，则四边形BKDQ是平行四边形，利用三角形角平分线性质定理可得KL＝，DL＝，过点B作BW⊥DF于点W，过点Q作QJ⊥DF于点J，则BW＝QJ＝，运用勾股定理可求得DW，BL，设MK＝x，则MW＝﹣x，再运用勾股定理和三角形角平分线性质定理建立方程求解即可．
【解答】解：（1）如图1，∵DA＝DB＝DC，
∴∠DAB＝∠DBA，∠DAC＝∠DCA，∠DBC＝∠DCB，
∴∠ADB＝180°﹣2∠DAB，∠BDC＝180°﹣2∠DCB，
∴∠ADC＝360°﹣2∠DAB﹣2∠DCB，
∴∠DCA＝∠DAC＝∠DAB+∠DCB﹣90°，
∴∠ACB＝∠DCB﹣∠DCA＝90°﹣∠DAB，
∴∠ADB＝2∠ACB；
（2）如图2，在AC上截取AQ＝CG，连接DQ，
∵∠BAC＝30°，
∴由（1）的方法，同理可求∠BDC＝2∠BAC＝60°，
∵BD＝CD，
∴△BCD是等边三角形，
∴∠DBC＝∠BDC＝60°，
又∵CD＝BD，BF＝DE，
∴△CDE≌△DBF（SAS），
∴∠BDF＝∠DCE，
∴∠BDC＝∠BDF+∠CDG＝∠DCE+∠CDG＝∠DGQ＝60°，
设CG＝3a，DG＝5a，
∵DA＝DC，
∴∠DAQ＝∠DCG，
又∵AQ＝CG，
∴△DAQ≌△DCG（SAS），
∴DG＝DQ＝5a，
∴△DGQ是等边三角形，
∴DQ＝QG＝5a，
∴AG＝8a，
∴AG＝DG；
（3）设∠BCE＝β，
由（2）知：∠DGE＝60°，
∴∠CGF＝60°，
∴∠BFD＝∠CGF+∠BCE＝60°+β，
∵2∠BNC﹣2∠BFD＝∠BCE，
∴2∠BNC﹣2（60°+β）＝β，
∴∠BNC＝60°+β，
∵∠BNC＝∠BDC+∠DBN＝60°+∠DBN，
∴∠DBN＝β，
∵∠CDF+∠DCG＝∠BCE+∠DCG＝60°，
∴∠CDF＝∠BCE＝β，
作BK∥DQ交DF于点K，作BL平分∠DBK交DF于点L，
则四边形BKDQ是平行四边形，
∴BK＝DQ＝5，DK＝BQ＝3，
∵BL平分∠DBK，
∴＝＝，
∵KL+DL＝3，
∴KL＝，DL＝，
过点B作BW⊥DF于点W，过点Q作QJ⊥DF于点J，
则BW＝QJ＝，
∴DW＝＝＝，
∴LW＝DW﹣DL＝﹣＝，KW＝DW﹣DK＝﹣3＝，
∴BL＝＝＝，
设MK＝x，则MW＝﹣x，
∵∠LBK＝∠KBM＝β，
∴＝，即＝，
∴BM＝x，
∵BW2+MW2＝BM2，
∴（）2+（﹣x）2＝（x）2，
解得：x1＝1，x2＝﹣（舍去），
∴MK＝1，
∴DM＝DL+KL+MK＝++1＝4．



【点评】本题是四边形综合题，考查了等腰三角形的性质，全等三角形的判定和性质，等边三角形判定和性质，三角形角平分线性质定理，勾股定理，平行四边形的判定与性质等；综合性强，难度大，添加辅助线构造直角三角形和全等三角形是解题关键．
25．（13分）（1）【操作发现】
如图1，将△ABC绕点A顺时针旋转50°，得到△ADE，连接BD，则∠ABD＝　65　度．

（2）【解决问题】
①如图2，在边长为的等边三角形ABC内有一点P，∠APC＝90°，∠BPC＝120°，求△APC的面积．
②如图3，在△ABC中，∠ACB＝90°，AC＝BC，P是△ABC内的一点，若PB＝1，PA＝3，∠BPC＝135°，则PC＝　2　．
（3）【拓展应用】
如图4是A，B，C三个村子位置的平面图，经测量AB＝4，BC＝3，∠ABC＝75°，P为△ABC内的一个动点，连接PA，PB，PC．求PA+PB+PC的最小值．
【分析】（1）【操作发现】：如图1中，根据旋转的性质可得AD＝AB，由三角形内角和定理可求出答案；
（2）【解决问题】
①如图2中，将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，只要证明∠PP′C＝90°，利用勾股定理即可解决问题；
②如图3中，将△CBP绕着点C按顺时针方向旋转90°，得到△CAP′，根据旋转的性质可以得到∠P′CP＝∠ACB＝90°，进而得到等腰直角三角形，求出PP'即可得出答案；
（3）【拓展应用】
如图4中，将△APB绕BC顺时针旋转60°，得到△EDB，连接PD、CE．得出∠CBE＝135°，过点E作EF⊥CB交CB的延长线于点F，求出CF和EF的长，可求出CE长，则答案可求出．
【解答】（1）【操作发现】
解：如图1中，

∵△ABC绕点A顺时针旋转50°，得到△ADE，
∴AD＝AB，∠DAB＝50°，
∴＝65°，
故答案为：65．

（2）【解决问题】
①解：如图2中，∵将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，

∴△APP′是等边三角形，∠AP′C＝∠APB＝360°﹣90°﹣120°＝150°，
∴PP′＝AP，∠AP′P＝∠APP′＝60°，
∴∠PP′C＝90°，∠P′PC＝30°，
∴PP′＝PC，即AP＝PC，
∵∠APC＝90°，
∴AP2+PC2＝AC2，即（PC）2+PC2＝（）2，
∴PC＝2，
∴AP＝，
∴S△APC＝AP•PC＝××2＝．

②如图3，将△CBP绕着点C按顺时针方向旋转90°，得到△CAP′，

∵CP′＝CP，∠P′CP＝∠ACB＝90°，
∴△P′CP为等腰直角三角形，
∴∠CP'P＝45°，
∵∠BPC＝135°＝∠AP'C，
∴∠AP′P＝90°，
∵PA＝3，PB＝1，
∴AP′＝1，
∴PP′＝＝＝2，
∴PC＝＝＝2．
故答案为：2．
（3）【拓展应用】
解：如图4中，将△APB绕B顺时针旋转60°，得到△EDB，连接PD、CE．

∵将△APB绕B顺时针旋转60°，得到△EDB，
∴∠ABP＝∠EBD，AB＝EB＝4，∠PBD＝60°，
∴∠ABP+∠PBC＝∠EBD+∠PBC，
∴∠EBD+∠PBC＝∠ABC＝75°，
∴∠CBE＝135°，
过点E作EF⊥CB交CB的延长线于点F，
∴∠EBF＝45°，
∴，
在Rt△CFE中，∵∠CFE＝90°，BC＝3，EF＝2，
∴＝
即PA+PB+PC的最小值为．
【点评】本题是几何变换综合题，考查了旋转变换的性质，等腰三角形的性质，等边三角形的性质，等腰直角三角形的性质，三角形的面积，勾股定理等知识，解题的关键是添加常用辅助线，构造直角三角形解决问题．

日期：2022/2/7 0:32:47；用户：初中账号6；邮箱：；学号：39888718