

初中数学中考复习 专题04 一元二次方程及应用(原卷版)
展开这是一份初中数学中考复习 专题04 一元二次方程及应用(原卷版),共7页。
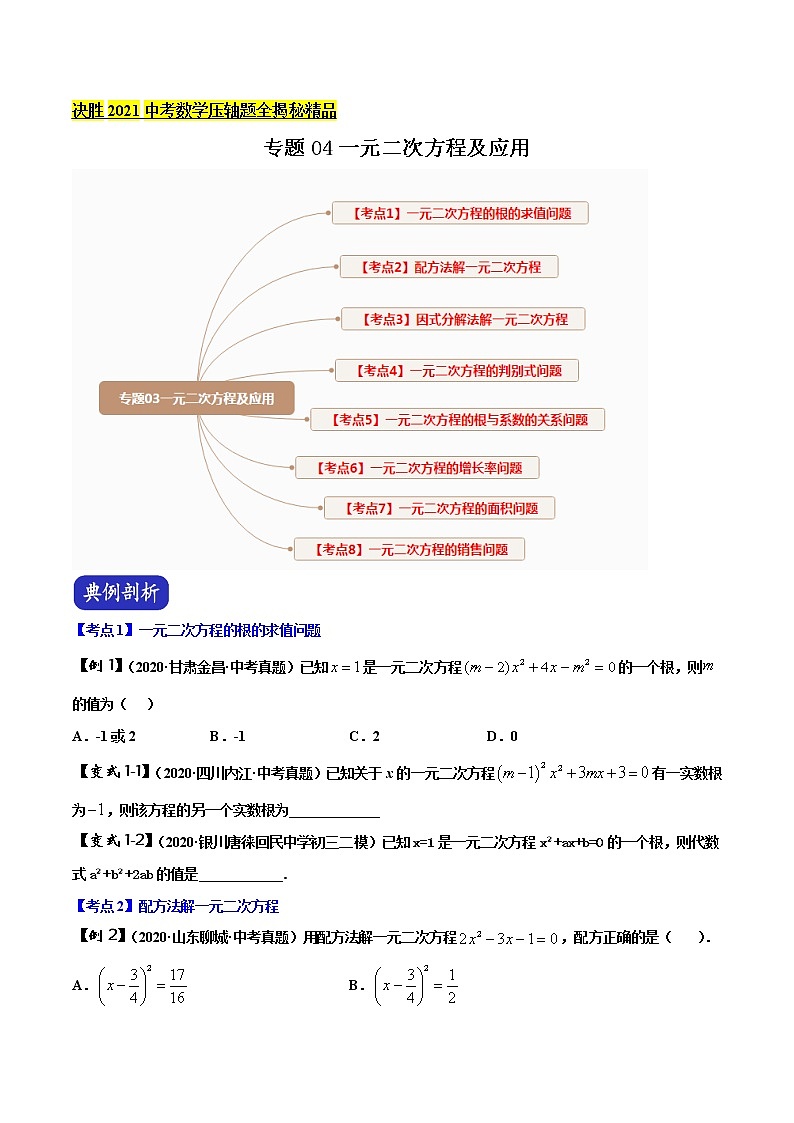
【考点1】一元二次方程的根的求值问题
【例1】(2020·甘肃金昌·中考真题)已知是一元二次方程的一个根,则的值为( )
A.-1或2B.-1C.2D.0
【变式1-1】(2020·四川内江·中考真题)已知关于x的一元二次方程有一实数根为,则该方程的另一个实数根为_____________
【变式1-2】(2020·银川唐徕回民中学初三二模)已知x=1是一元二次方程x²+ax+b=0的一个根,则代数式a²+b²+2ab的值是____________.
【考点2】配方法解一元二次方程
【例2】(2020·山东聊城·中考真题)用配方法解一元二次方程,配方正确的是( ).
A.B.
C.D.
【变式2-1】(2020·山东泰安·中考真题)将一元二次方程化成(a,b为常数)的形式,则a,b的值分别是( )
A.,21B.,11C.4,21D.,69
【考点3】因式分解法解一元二次方程
【例3】(2020·山东威海·中考真题)一元二次方程的解为__________.
【变式3-1】(2019•十堰)对于实数a,b,定义运算“◎”如下:a◎b=(a+b)2﹣(a﹣b)2.若(m+2)◎(m﹣3)=24,则m= .
【变式3-2】(2020·湖南中考真题)阅读理解:对于x3﹣(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
x3﹣(n2+1)x+n=x3﹣n2x﹣x+n=x(x2﹣n2)﹣(x﹣n)=x(x﹣n)(x+n)﹣(x﹣n)=(x﹣n)(x2+nx﹣1).
理解运用:如果x3﹣(n2+1)x+n=0,那么(x﹣n)(x2+nx﹣1)=0,即有x﹣n=0或x2+nx﹣1=0,
因此,方程x﹣n=0和x2+nx﹣1=0的所有解就是方程x3﹣(n2+1)x+n=0的解.
解决问题:求方程x3﹣5x+2=0的解为_____.
【考点4】一元二次方程的判别式问题
【例4】(2020·内蒙古呼伦贝尔·中考真题)已知关于的一元二次方程有实数根,则的取值范围是___________.
【变式4-1】(2020·黑龙江大庆·中考真题)已知关于的一元二次方程,有下列结论:
①当时,方程有两个不相等的实根;
②当时,方程不可能有两个异号的实根;
③当时,方程的两个实根不可能都小于1;
④当时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为_________.
【变式4-2】(2020·湖北鄂州·中考真题)已知关于x的方程有两实数根.
(1)求k的取值范围;
(2)设方程两实数根分别为、,且,求实数k的值.
【考点5】一元二次方程的根与系数的关系问题
【例5】(2020·四川眉山·中考真题)设,是方程的两个实数根,则的值为______.
【变式5-1】(2020·贵州黔南·中考真题)对于实数a,b,定义运算“”,例如,因为,所以.若是一元二次方程的两个根,则_________.
【变式5-2】(2020·湖北随州·中考真题)已知关于的一元二次方程.
(1)求证:无论取何值,此方程总有两个不相等的实数根;
(2)若方程有两个实数根,,且,求的值.
【考点6】一元二次方程的增长率问题
【例6】(2020·湖南湘西·中考真题)某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.
(1)求口罩日产量的月平均增长率;
(2)按照这个增长率,预计4月份平均日产量为多少?
【变式6-1】(2020·上海中考真题)去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的12%.
(1)求该商店去年“十一黄金周”这七天的总营业额;
(2)去年,该商店7月份的营业额为350万元,8、9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等.求该商店去年8、9月份营业额的月增长率.
【考点7】一元二次方程的面积问题
【例7】(2020·西藏中考真题)列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
【变式7-1】(2020·山西中考真题)如图是一张长,宽的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是的有盖的长方体铁盒.则剪去的正方形的边长为______.
【考点8】一元二次方程的销售问题
【例8】(2020·山东郯城·初三零模)九龙坡区某社区开展全民读书活动,以丰富人们业余文化生活现计划筹资30000元用于购买科普书籍和文艺刊物
(1)计划购买文艺刊物的资金不少于购买科普书籍资金的2倍,那么最少用多少资金购买文艺刊物?
(2)经初步了解,有200户居民自愿参与集资,那么平均每户需集资150元.经筹委会进步宣传,自愿参加的户数在200户的基础上增加了a%(其中a>50),如果每户平均集资在150元的基础上减少a%,那么实际筹资将比计划筹资多6000元,求a的值.
【变式8-1】(2020·山东滨州·中考真题)某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.
(1)当售价为55元/千克时,每月销售水果多少千克?
(2)当月利润为8750元时,每千克水果售价为多少元?
(3)当每千克水果售价为多少元时,获得的月利润最大?
1.(2020·贵州遵义·中考真题)已知x1,x2是方程x2﹣3x﹣2=0的两根,则x12+x22的值为( )
A.5B.10C.11D.13
2.(2020·辽宁营口·中考真题)一元二次方程x2﹣5x+6=0的解为( )
A.x1=2,x2=﹣3B.x1=﹣2,x2=3
C.x1=﹣2,x2=﹣3D.x1=2,x2=3
3.(2020·广西河池·中考真题)某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )
A.6B.7C.8D.9
4.(2020·甘肃金昌·中考真题)已知是一元二次方程的一个根,则的值为( )
A.-1或2B.-1C.2D.0
5.(2020·湖南衡阳·中考真题)如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为米,则根据题意,列方程为( )
A.B.
C.D.
6.(2020·湖南张家界·中考真题)已知等腰三角形的两边长分别是一元二次方程的两根,则该等腰三角形的底边长为( )
A.2B.4C.8D.2或4
7.(2020·江苏南京·中考真题)关于x的方程(为常数)根的情况下,下列结论中正确的是( )
A.两个正根B.两个负根
C.一个正根,一个负根D.无实数根
8.(2020·郑州枫杨外国语学校)用配方法解一元二次方程2x2-4x-2=1的过程中,变形正确的是( )
A.2(x-1)2=1B.2(x-1)2=5C.(x-1)2=D.(x-2)2=
9.(2020·贵州毕节·中考真题)关于的一元二次方程有一个根是,则的值是_______.
10.(2020·山东东营·中考真题)如果关于的一元二次方程有实数根,那么的取值范围是___.
11.(2020·四川宜宾·中考真题)一元二次方程的两根为,则________________
12.(2020·湖北荆门·中考真题)已知关于x的一元二次方程的一个根比另一个根大2,则m的值为_____.
13.(2020·江苏常州·中考真题)若关于x的方程有一个根是1,则_________.
14.(2020·四川成都·中考真题)关的一元二次方程有实数根,则实数的取值范围是_________.
15.(2020·江苏无锡·中考真题)解方程:
(1) (2)
16.(2020·山东博山·初三二模)用配方法求一元二次方程的实数根.
17.(2020·湖北黄石·中考真题)已知:关于x的一元二次方程有两个实数根.
(1)求m的取值范围;
(2)设方程的两根为、,且满足,求m的值.
18.(2020·山东蒙阴·初三一模)为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
19.(2019·辽宁锦州·中考真题)2019年在法国举办的女足世界杯,为人们奉献了一场足球盛宴.某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可售出100件.根据市场行情,现决定涨价销售,调查表明,每件商品的售价每上涨1元,每个月会少售出2件,设每件商品的售价为x元,每个月的销量为y件.
(1)求y与x之间的函数关系式;
(2)当每件商品的售价定为多少元时,每个月的利润恰好为2250元;
(3)当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?
相关试卷
这是一份初中数学中考复习 专题11 一元二次方程及其应用(原卷版),共7页。试卷主要包含了一元二次方程的定义,一元二次方程的一般形式,一元二次方程的根,一元二次方程的解法,2=9的根是 等内容,欢迎下载使用。
这是一份初中数学中考复习 专题09 一元二次方程及其应用(原卷版),共7页。试卷主要包含了定义等内容,欢迎下载使用。
这是一份初中数学中考复习 专题04 一元二次方程及其应用(原卷版),共4页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。












