专题05 锐角三角函数（重点）-2022-2023学年九年级数学下册期中期末挑战满分冲刺卷（苏科版，江苏专用）

专题05 锐角三角函数（重点）

一、单选题

1．（    ）

A．2 B． C． D．

2．在中，，，，那么下列结论正确的是（   ）

A． B． C． D．

3．如果锐角的正切值为，那么下列结论中正确的是（　　　）

A． B． C． D．

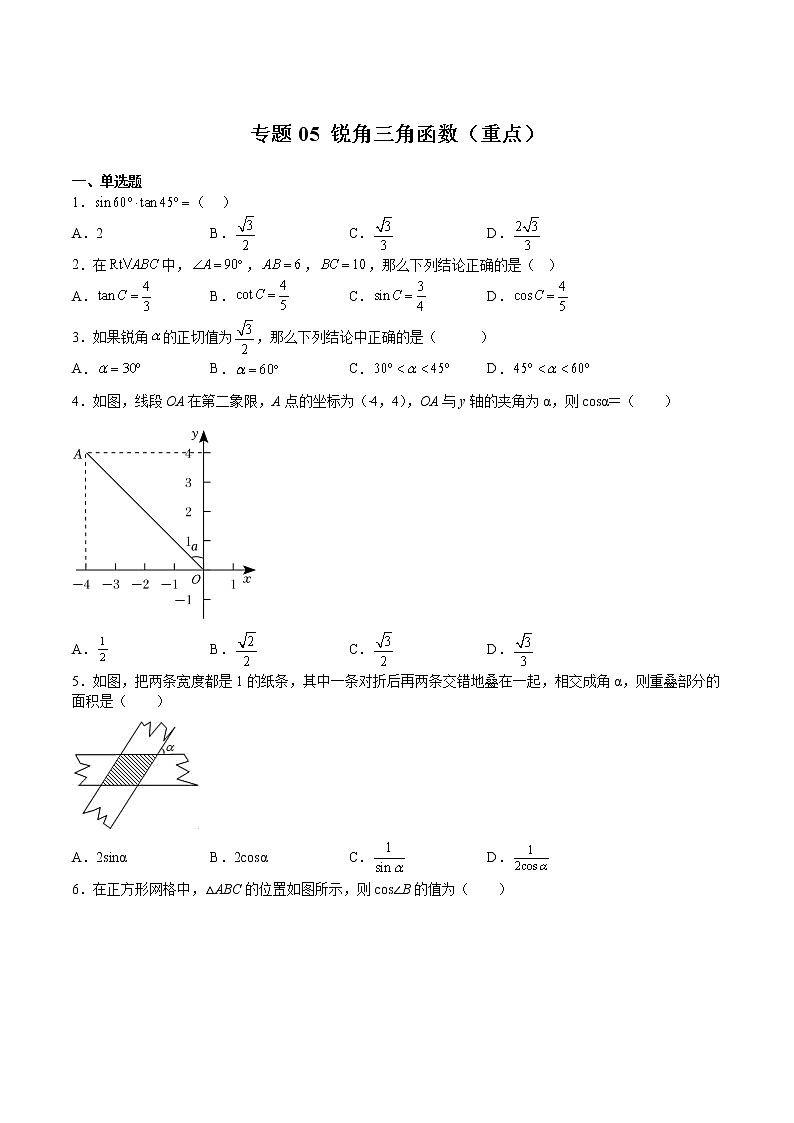
4．如图，线段OA在第二象限，A点的坐标为（﹣4，4），OA与y轴的夹角为α，则cosα＝（　　）

A． B． C． D．

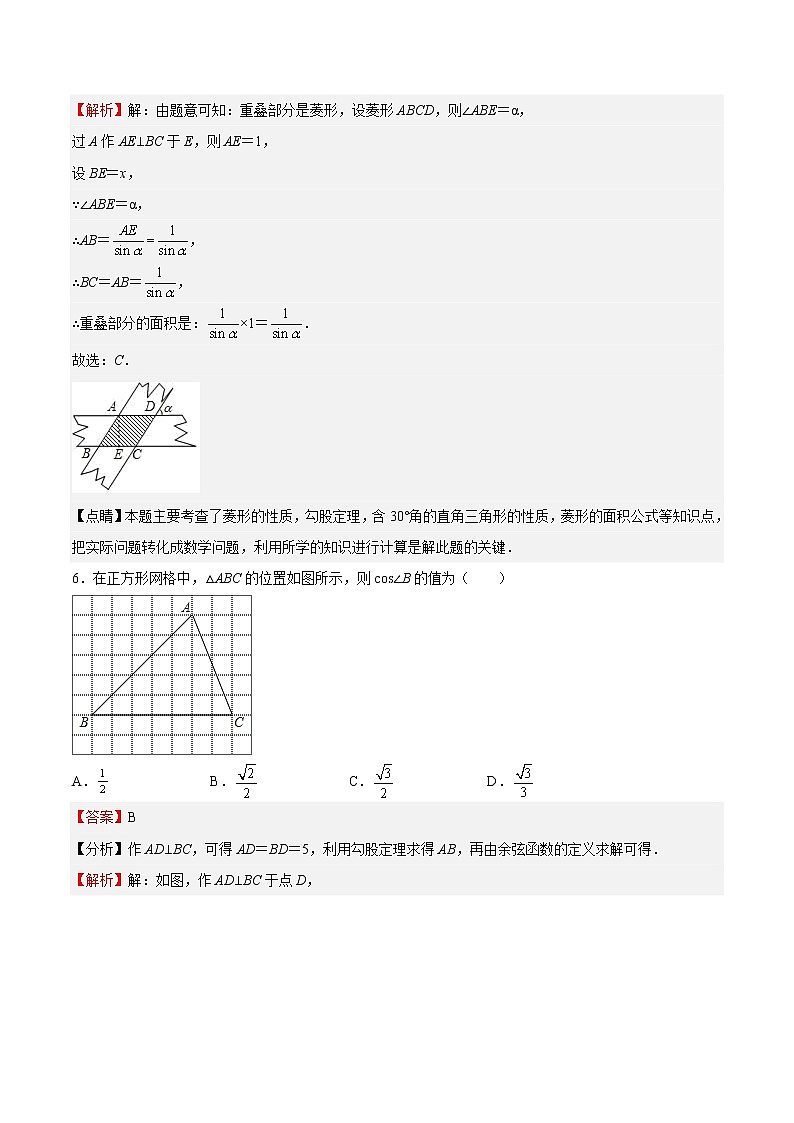
5．如图，把两条宽度都是1的纸条，其中一条对折后再两条交错地叠在一起，相交成角α，则重叠部分的面积是（　　）

A．2sinα B．2cosα C． D．

6．在正方形网格中，△ABC的位置如图所示，则cos∠B的值为（　　）

A． B． C． D．

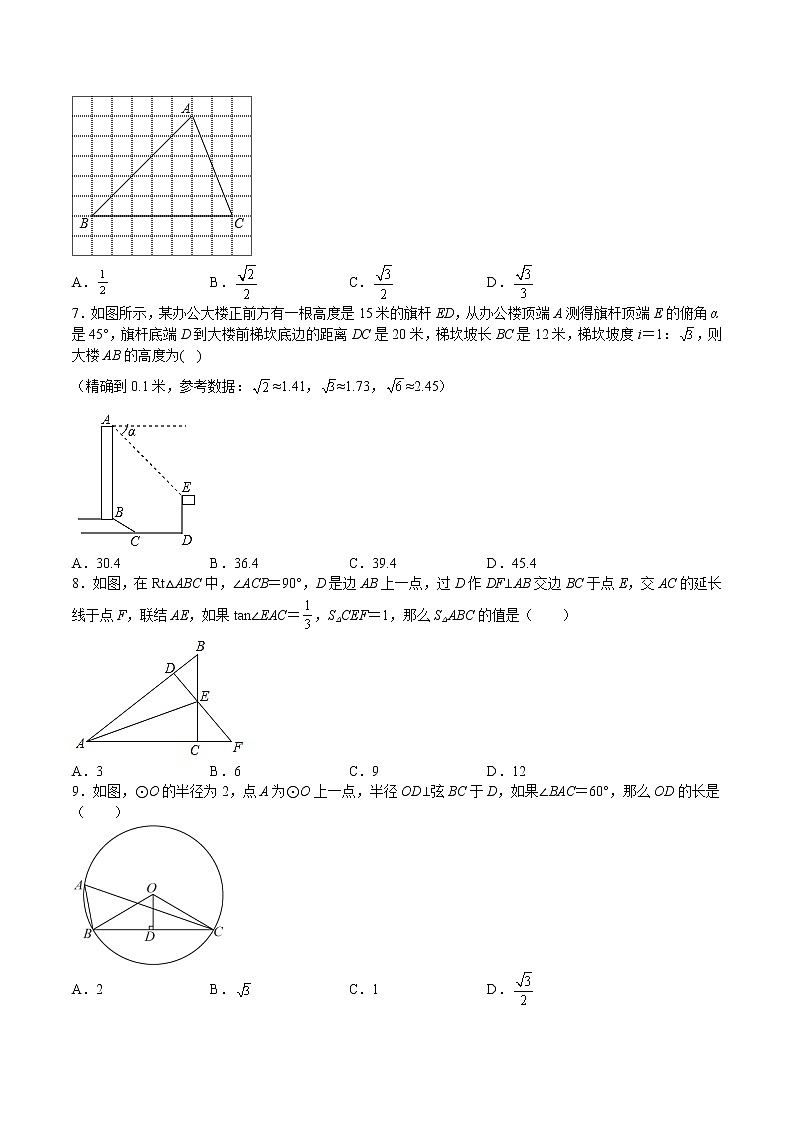
7．如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i＝1：，则大楼AB的高度为(   )

（精确到0.1米，参考数据：≈1.41，≈1.73，≈2.45）

A．30.4 B．36.4 C．39.4 D．45.4

8．如图，在Rt△ABC中，∠ACB＝90°，D是边AB上一点，过D作DF⊥AB交边BC于点E，交AC的延长线于点F，联结AE，如果tan∠EAC＝，S△CEF＝1，那么S△ABC的值是（　　）

A．3 B．6 C．9 D．12

9．如图，⊙O的半径为2，点A为⊙O上一点，半径OD⊥弦BC于D，如果∠BAC＝60°，那么OD的长是（　　）

A．2 B． C．1 D．

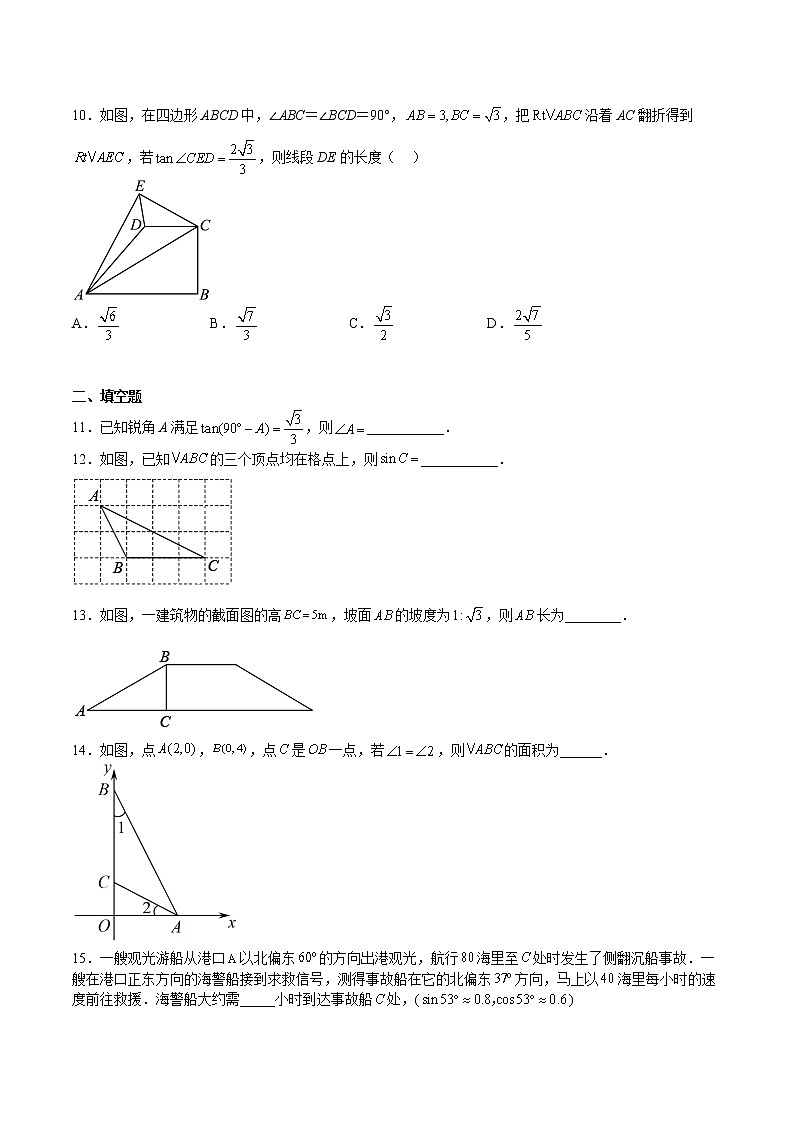
10．如图，在四边形ABCD中，∠ABC＝∠BCD＝90°，，把沿着AC翻折得到，若，则线段DE的长度（    ）

A． B． C． D．

二、填空题

11．已知锐角A满足，则___________．

12．如图，已知的三个顶点均在格点上，则___________．

13．如图，一建筑物的截面图的高，坡面的坡度为，则长为________．

14．如图，点，，点是一点，若，则的面积为______．

15．一艘观光游船从港口以北偏东的方向出港观光，航行海里至处时发生了侧翻沉船事故．一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东方向，马上以海里每小时的速度前往救援．海警船大约需_____小时到达事故船处，()

16．如图，在直角中，，点从点出发沿线段向点移动，连接交边于点．若，那么线段________．

17．如图，线段，C为线段上的一个动点，以为边作等边和等边连接，外接于，则半径的最小值为______．

18．如图，在 中，，，， 平分 交 于点 ，点 为 上一点，作 交 于点 ，若 ，则 的长是____．

三、解答题

19．计算：

(1)；

(2)．

20．如图，在中，，，，．

(1)求和的长；

(2)求的值．

21．在正方形网格中，仅用无刻度直尺按下列要求作图．

(1)如图①中，在AB上找点C，使得AC：BC＝2：3；

(2)在图②中作∠DAB，使得tan∠DAB＝．（保留作图痕迹）

22．如图，在中，弦垂直于半径，垂足为点E，点D是优弧上一点，连接．

(1)求的度数．

(2)若，求图中劣弧的长．

23．如图，在中，，，点在边AC上，且，，垂足为点，联结，求：

(1)线段的长；

(2)的余弦值．

24．如图，已知点A、B、C在上，点D在外，，交于E点．

(1)求证：是的切线；

(2)若的半径为5，，求线段的长．

25．六府塔公园因其是隋代建筑“六府塔”遗址而得名，坐落于长治市城区解放西街北侧西寺巷，现今遗存的残塔仅剩塔座部分，后经市委市政府修缮，在塔基的旁边重新修建了一座六府塔，现在早已成为了人们休闲纳凉锻炼的场所．周日实验中学学生想用一些测量工具和所学的几何知识测量新六府塔的高度，并检验自己掌握知识和应用知识的能力．他们携带的工具有：小镜子，卷尺，标杆，测角仪等．

如图：小王在小张和六府塔之间的直线上平放一个平面镜，在镜面上做了一个标记，这个标记在直线上对应位置为点C，镜子不动，小张看着镜面上的标记，他来回走动，走到点D时，看到塔顶端点A在镜面中的像与镜面上的标记重合，同时小王用测角仪测量，测得以下数据：

①，②，③点C处测得塔顶A处的仰角为；

然后小张从点D沿方向走了，到达塔影的末端F处，在F处放置一根标杆，此时标杆的影长为，测得以下数据：

④，⑤，⑥点F处测得塔顶A处的仰角为；

如图：已知，其中，测量时使用的平面镜的厚度及测角仪的高度忽略不计，请你根据题目中的数据选择必须的数据计算六府塔的高度．

(1)你所选的数据是__________________________（注意：填序号，但你所选的数据必须用到，多选或者少选均不得分）

(2)计算过程：（参考数据：）

26．如图，在⊙O中，AB是直径，P为AB上一点，过点P作弦MN，.

(1)（如图1）若AP=2，BP=6，且OH⊥MN，则⊙O的半径OB=___________， OP=___________，OH=___________， MN=___________.

(2)（如图2）若MP=3，NP=5，求PB的长；

(3)当P在AB上运动时（不变），直接写出的值.

27．如图，在直角坐标平面内，直线与x轴和y轴分别交于A、B两点，二次函数的图象经过点A、B，且顶点为C．

(1)求这个二次函数的解析式；

(2)求的值；

(3)若M是这个二次函数图象上位于x轴下方的一点，且的面积为40，求点M的坐标．

28．已知，在中，，，，点、分别在边、上，且均不与顶点重合，（如图1所示），设，．

(1)当点与点重合时（如图2所示），求线段的长；

(2)在图1中当点不与点重合时，求关于的函数解析式及其定义域；

(3)我们把有一组相邻内角相等的凸四边形叫做等邻角四边形．请阅读理解以上定义，完成问题探究：如图1，设点在边上，，如果四边形是等邻角四边形，求线段的长．

29．如图，在矩形中，，，点从点出发沿以的速度向点移动；同时，点从点出发沿以的速度向点移动．当点与点重合时两点都停止移动，时间为．

(1)如图1，若时，求时间的值：

(2)如图2，连接，作，垂足为点，作的外接圆．

①判断点与的位置关系，并说明理由．

②连接、，若的面积等于9，求的值．