





专题14 与圆有关的性质(课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用)
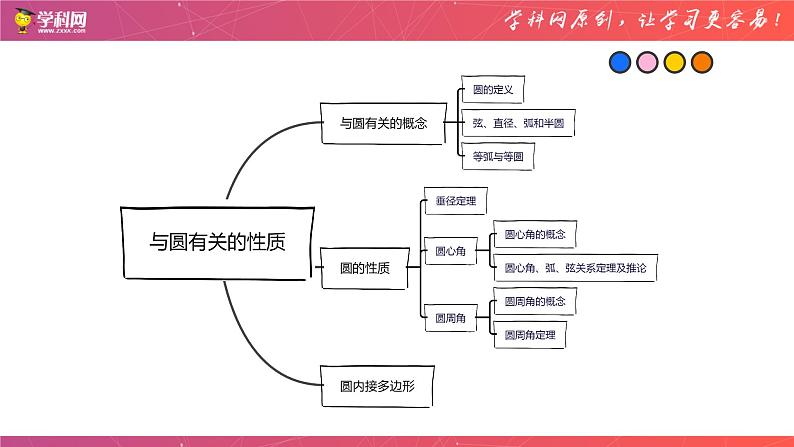
展开旋转方式定义:如图,在一个平面内,线段OA绕着它固定的一个端点O旋转一周,另一个端点A所形成的图形叫作圆.固定的端点O叫作圆心,线段OA叫作半径,记作⊙O,读作“圆O”。
集合方式定义:在一个平面内,到定点的距离等于定长的所有点的集合叫作圆,定点为圆心,定长为半径。
【知识拓展】1.圆心确定圆的位置,半径确定圆的大小。
2.确定一个圆应先确定圆心,再确定半径,二者缺一不可。
3.圆是一条封闭曲线。
弦:连接圆上任意两点的线段叫作弦.如图中的AB,AC。
直径:经过圆心的弦叫作直径.如图中的AB。
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫作半圆。
等圆:能够重合的两个圆叫作等圆。
等弧:在同圆或等圆中,能够互相重合的弧叫作等弧。
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径。
【知识拓展】在垂径定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,这5个条件中,知道任意2个,就能推出其他3项结论。
圆心角的定义:顶点在圆心的角叫作圆心角,如图中的∠BOC.
圆心角、弧、弦关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角、弧、弦关系定理推论1:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,它们所对的弦也相等。
【知识拓展】使用圆心角定理时,不要忽略“同圆或等圆”这个条件,若两个圆的半径不相等(不是同圆或等圆),则相等的圆心角所对的弦、弧不相等。
圆心角、弧、弦关系定理推论2:在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,它们所对应的弧也相等。
2.应用“在同圆或等圆中,相等的弦所对的弧相等”这个定理时,两条弧应同为优弧或同为劣弧。
圆周角的定义:顶点在圆上,两边都和圆相交的角叫作圆周角。如图中的∠A和∠D。
圆周角定理推论1:同弧或等弧所对的圆周角相等,如图∠A=∠D。
圆周角定理推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径,如图∠AEB=90°。
圆内接多边形的定义:如果一个多边形的所有顶点都在同一个圆上,那么这个多边形叫作这个圆的内接多边形,这个圆叫作这个多边形的外接圆。
圆内接四边形的性质:圆内接四边形的对角互补。
【补充】根据圆内接四边形的性质可以得出:圆内接四边形任何一个外角等于它的内对角。
备战2024年中考数学一轮复习精品课件与题型归纳专练(全国通用) 专题16 与圆有关的计算(课件)+专题特训资料+(解析): 这是一份备战2024年中考数学一轮复习精品课件与题型归纳专练(全国通用) 专题16 与圆有关的计算(课件)+专题特训资料+(解析),文件包含备战2024年中考数学一轮复习精品课件与题型归纳专练全国通用专题16与圆有关的计算课件pptx、备战2024年中考数学一轮复习精品课件与题型归纳专练全国通用专题16与圆有关的计算题型归纳原卷版+解析docx等2份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
专题17 相似(课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用): 这是一份专题17 相似(课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用),共39页。PPT课件主要包含了图形相似的概念,相似多边形,比例线段,比例的基本性质,黄金分割,考点2相似三角形,平行线分线段成比例,相似三角形的定义,相似三角形的性质,相似三角形的判定等内容,欢迎下载使用。
专题16 与圆有关的计算(课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用): 这是一份专题16 与圆有关的计算(课件)-备战2023年中考数学一轮复习精品课件与题型归纳专练(全国通用),共31页。PPT课件主要包含了考点1正多边形和圆,正多边形的有关概念,正n边形的画法,正多边形的有关计算,弧长公式,扇形面积公式,圆锥及其展开图,圆锥的有关计算,强化训练等内容,欢迎下载使用。