



2023高三数学二轮热点题型专项突破专题20 立体几何中的探索性问题(新高考全国通用)
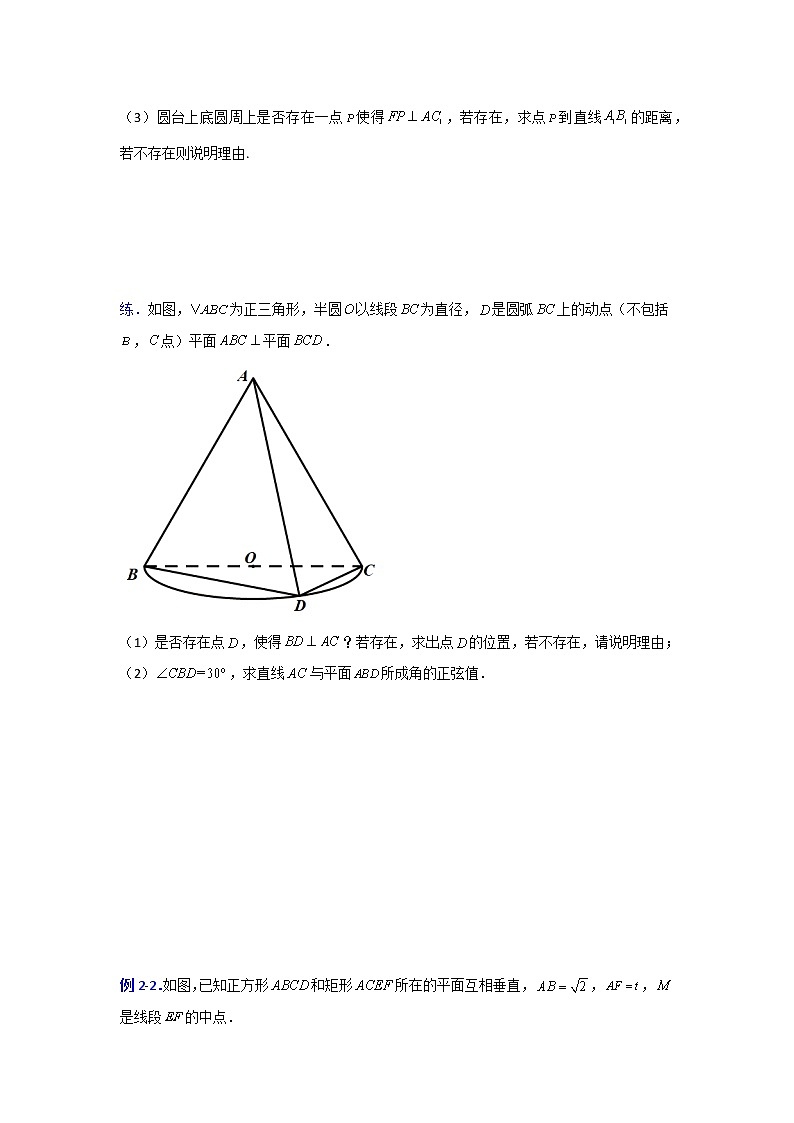
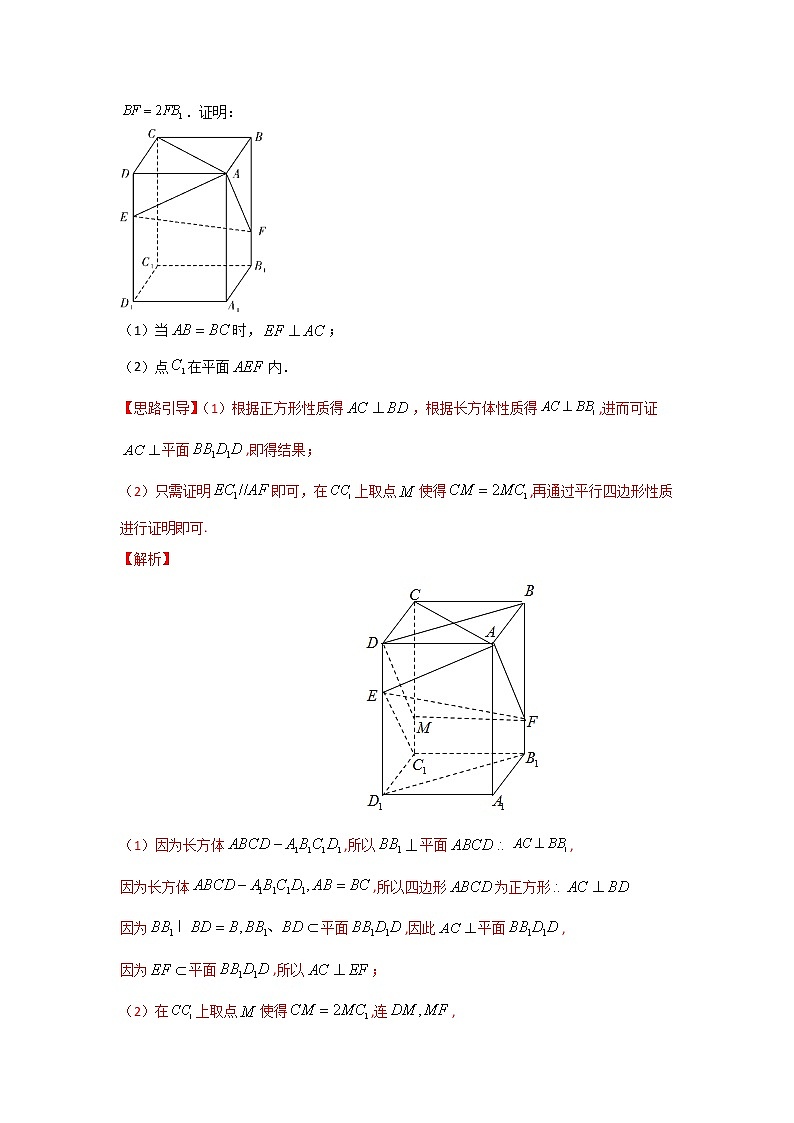
展开立体几何中的探索性问题高考定位立体几何中的探索性问题是高考几何的一个难点,尤常见于新高考的多选题和解答题中,其题目特点是灵活性较强,需要相对丰富的空间想象能力及计算能力,对所研究几何体进行深入的剖析与推理。专题解析本专题研究解答题中的探索性问题:点的存在性(1)探索共面(2)探索线线平行与垂直(3)探索线面平行与垂直(4)探索面面平行与垂直(5)探索线面角定值与最值(6)探索面面角定值与最值(7)探索距离面积体积定值专项突破类型一、探索共面例1-1.如图,四棱锥的底面为平行四边形,,分别为,的中点.(1)求证:平面.(2)在线段上是否存在一点使得,,,四点共面?若存在,求出的值;若不存在,请说明理由.练. 如图,在长方体中,点,分别在棱,上,且,.证明:(1)当时,;(2)点在平面内.类型二、探索线线关系例2-1.在滨海文化中心有天津滨海科技馆,其建筑有鲜明的后工业风格,如图所示,截取其中一部分抽象出长方体和圆台组合,如图所示,长方体中,,圆台下底圆心为的中点,直径为2,圆与直线交于,圆台上底的圆心在上,直径为1.(1)求与平面所成角的正弦值;(2)求二面角的余弦值;(3)圆台上底圆周上是否存在一点使得,若存在,求点到直线的距离,若不存在则说明理由.练.如图,为正三角形,半圆以线段为直径,是圆弧上的动点(不包括,点)平面平面.(1)是否存在点,使得?若存在,求出点的位置,若不存在,请说明理由;(2),求直线与平面所成角的正弦值.例2-2.如图,已知正方形和矩形所在的平面互相垂直,,,是线段的中点.(1)求证:平面;(2)若,求二面角的大小;(3)若线段上总存在一点,使得,求的最大值.练.如图,在四棱锥中,底面是矩形,,,底面.(1)当为何值时,平面?证明你的结论;(2)若在边上至少存在一点,使,求的取值范围.例2-3.如图所示,在中,斜边,,将沿直线AC旋转得到,设二面角的大小为.(1)取AB的中点E,过点E的平面与AC,AD分别交于点F,G,当平面平面BDC时,求FG的长;(2)当时,求二面角的余弦值.(3)是否存在,使得?若存在,求出的值;若不存在,说明理由.练.如图,在四棱锥中,底面是平形四边形,设∠ABC=θ,平面,点为的中点,且,PA=AD=2.(1)若θ=45°,求二面角P-BC-A的正切值;(2)是否存在使PM⊥BD,若存在求出,若不存在请说明理由.例2-4(恒).如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,且斜边AB=22,侧棱AA1=3,点为的中点,点在线段上,AE=λAA1(λ 为实数).(1)求证:不论λ取何值时,恒有CD⊥B1E;(2)当λ=13时,求平面与平面所成二面角的余弦值.练.如图,四棱锥的底面是正方形,平面,,AD=2a,点是上的点,且DE=λa(0<λ≤2).(1)求证:对任意的λ∈(0,2],都有AC⊥BE.(2)设二面角的大小为θ,直线与平面所成的角为φ,若,求λ的值.类型三、探索线面关系例3-1.(2018年全国卷Ⅲ文数高考试题)如图,矩形所在平面与半圆弧所在平面垂直,是上异于,的点.(1)证明:平面平面;(2)在线段上是否存在点,使得平面?说明理由.练.如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD.(Ⅰ)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由; (Ⅱ)证明:平面PAB⊥平面PBD.练.七面体玩具是一种常见的儿童玩具.在几何学中,七面体是指由七个面组成的多面体,常见的七面体有六角锥、五角柱、正三角锥柱、Szilassi多面体等.在拓扑学中,共有34种拓扑结构明显差异的凸七面体,它们可以看作是由一个长方体经过简单切割而得到的.在如图所示的七面体中,平面(1)在该七面体中,探究以下两个结论是否正确.若正确,给出证明;若不正确,请说明理由:①平面;②平面;(2)求该七面体的体积.例3-2.如图,在四棱锥中,底面是正方形,侧面底面,,分别为中点,.(1)求证:平面;(2)求二面角的余弦值;(3)在棱上是否存在一点,使平面?若存在,指出点的位置;若不存在,说明理由.类型四、探索面面平行与垂直例4-1.如图,在三棱柱中,平面,,E,F分别为,的中点.(Ⅰ)在四边形内是否存在点G,使平面平面?若存在,求出该点的位置;若不存在,请说明理由;(Ⅱ)设D是的中点,求与平面所成角的正弦值.例4-2. 如图所示,在四棱锥中,平面,,,,为的中点.(1)求证平面;(2)若点为的中点,线段上是否存在一点,使得平面平面?若存在,请确定的位置;若不存在,请说明理由.例4-3(恒垂直).已知四棱锥中,底面是边长为2的菱形,且,平面,、分别是、上的中点,直线与平面所成角的正弦值为,点在上移动.(1)证明:无论点在上如何移动,平面平面;(2)若点为的中点,求二面角的余弦值.类型五、探索线面角例5-1.如图,四棱锥中,底面为菱形,,,平面,.(1)点E在线段PC上,,点F在线段PD上,,求证:平面;(2)设M是直线AC上一点,求CM的长,使得MP与平面PCD所成角为.例5-2.如图,已知矩形所在平面垂直于直角梯形所在平面,且,,,且(1)设点M为棱中点,求证平面;(2)线段上是否存在一点N,使得直线与平面所成角的正弦值等?若存在,试求出线段的长度;若不存在,请说明理由.例5-3.直角梯形绕直角边旋转一周的旋转的上底面面积为,下底面面积为,侧面积为,且二面角为,,分别在线段,上.(Ⅰ)若,分别为,中点,求与所成角的余弦值;(Ⅱ)若为上的动点、为的中点,求与平面所成最大角的正切值,并求此时二面角的余弦值.练.如图,在四棱锥中,底面为正方形,侧棱底面,,,为的中点,点在棱上,且.(1)求直线与直线所成角的余弦值;(2)当直线与平面所成的角最大时,求此时的值.练.请从下面三个条件中任选一个,补充在下面的横线上,并作答.①;②;③点在平面的射影在直线上.如图,平面五边形中,是边长为的等边三角形,,,,将沿翻折成四棱锥,是棱上的动点(端点除外),分别是的中点,且___________.(1)求证:;(2)当与平面所成角最大时,求平面与平面所成的锐二面角的余弦值.注:如果选择多个条件分别解答,按第一个解答计分.练.如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,为底面圆的内接正三角形,且边长为在母线上,且.(1)求证:平面平面;(2)设线段上动点为,求直线与平面所成角的正弦值的最大值.练.如图,四棱锥的底面是边长为的正方形,.(1)证明:;(2)当直线与平面所成角的正弦值最大时,求此时二面角的大小.练.在①平面,②平面平面,③这三个条件中任选一个,补充在下面的问题中,并解决该问题.问题:如图,在三棱锥中,平面平面,是以为斜边的等腰直角三角形,,,为中点,为内的动点(含边界).(1)求点到平面的距离;(2)若__________,求直线与平面所成角的正弦值的取值范围.注:若选择多个条件分别解答,按第一个解答计分.类型六、探索面面角例6-1、如图,在半径为的半球O中,平行四边形是圆O的内接四边形,,点P是半球面上的动点,且四棱锥的体积为.(1)求动点P的轨迹T围成的面积;(2)是否存在点P使得二面角的大小为?请说明理由.例6-2(恒定角).如图1,菱形中,动点,在边,上(不含端点),且存在实数使,沿将向上折起得到,使得平面平面,如图2所示.(1)若,设三棱锥和四棱锥的体积分别为,,求;(2)试讨论,当点的位置变化时,二面角是否为定值,若是,求出该二面角的余弦值,若不是,说明理由.练.在四棱锥中,底面为菱形,,平面平面,是边长为2的正三角形,,分别为,的中点.(Ⅰ)证明:平面;(Ⅱ)在棱上是否存在一点,使得锐二面角的余弦值为?若存在,求出的值;若不存在,请说明理由.例6-2.某人设计了一个工作台,如图所示,工作台的下半部分是个正四棱柱ABCD﹣A1B1C1D1,其底面边长为4,高为1,工作台的上半部分是一个底面半径为的圆柱体的四分之一.(1)当圆弧E2F2(包括端点)上的点P与B1的最短距离为5时,证明:DB1⊥平面D2EF.(2)若D1D2=3.当点P在圆弧E2E2(包括端点)上移动时,求二面角P﹣A1C1﹣B1的正切值的取值范围.练.如图,矩形中,,将其沿翻折,使点到达点的位置,且二面角为直二面角.(1)求证:平面平面;(2)设是的中点,二面角的平面角的大小为,当时,求的取值范围.练;.如图所示,四棱锥的底面是边长为a的正方形,PB⊥平面ABCD.(1)若平面PAD与平面ABCD所成的二面角为60°,求这个四棱锥的体积.(2)求证:无论四棱锥的高怎样变化,平面PAD与平面PCD所成的二面角恒大于90°例6-3(恒).已知E,F分别为等腰直角三角形的边上的中点,∠ACB=900,AC=BC=4,现把ΔAEF沿折起(如图2),连结AB,AC,得到四棱锥A1-BCEF.(1)证明:无论把ΔAEF转到什么位置,面A1EF⊥面A1EC;(2)当四棱锥A1-BCEF的体积最大时,求到面A1BF的距离及体积的最大值.类型七、探索距离面积体积定值例7-1(定距离).如图,在棱长为2的正方体中,M是线段AB上的动点.(1)证明:平面;(2)若点M是AB中点,求二面角的余弦值;(3)判断点M到平面的距离是否为定值?若是,求出定值;若不是,请说明理由.例7-2(定体积).如图,是边长为的正方形,平面平面(1)证明:平面平面;(2)在上是否存在一点,使平面将几何体分成上下两部分的体积比为?若存在,求出点的位置;若不存在,请说明理由.例7-3.如图,在正三棱柱(侧面垂直于底面,且底面是正三角形)中,,是棱上一动点.(1)若,分别是,的中点,求证:平面;(2)求证:三棱锥的体积为定值,并求出该定值.例7-4.如图,已知点是三角形所在平面外一点,且,截面分别平行于,(点,,,分在棱,,,上)(1)求证:四边形是平行四边形且周长为定值;(2)设与所成角为,求四边形的面积的最大值.
2023高三数学二轮热点题型专项突破 专题27 圆锥曲线背景下定值的探索(新高考全国通用): 这是一份2023高三数学二轮热点题型专项突破 专题27 圆锥曲线背景下定值的探索(新高考全国通用),文件包含专题27圆锥曲线背景下定值的探索一题一专题技巧全突破2022高三二轮热点题型专项突破解析版docx、专题27圆锥曲线背景下定值的探索一题一专题技巧全突破2022高三二轮热点题型专项突破原卷版docx等2份教案配套教学资源,其中教案共114页, 欢迎下载使用。
2023高三数学二轮热点题型专项突破专题26 圆锥曲线背景下定点的探索(新高考全国通用): 这是一份2023高三数学二轮热点题型专项突破专题26 圆锥曲线背景下定点的探索(新高考全国通用),文件包含专题26圆锥曲线背景下定点的探索一题一专题技巧全突破2022高三二轮热点题型专项突破解析版docx、专题26圆锥曲线背景下定点的探索一题一专题技巧全突破2022高三二轮热点题型专项突破原卷版docx等2份教案配套教学资源,其中教案共37页, 欢迎下载使用。
2023高三数学二轮热点题型专项突破专题22 截面(新高考全国通用): 这是一份2023高三数学二轮热点题型专项突破专题22 截面(新高考全国通用)












