

七年级数学下册考点精练专题08 平行与折叠问题
展开专题08 平行与折叠问题
【模型讲解】
如图,Rt△ABC中,∠C=90°,∠A=30°,E,F分别是边AC,AB上的点,连接EF,将△AEF沿EF折叠,得到,当的边与△ABC的一边平行时,∠AEF的度数是_____.
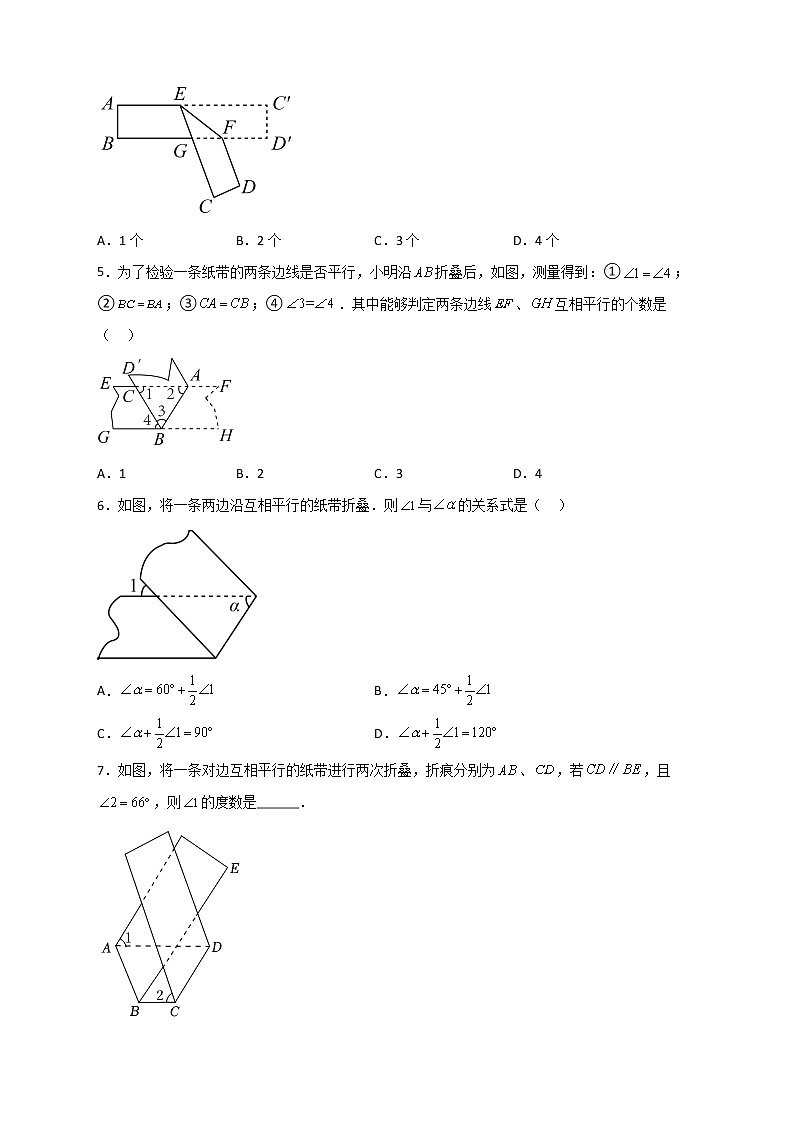
解:如图1,若时,∴,∵∠C=90°,∠A=30°,
∴,∵将△AEF沿EF折叠,得到,
∴,∴∠BFE=180°﹣∠AFE,
∴∠AFE﹣60°=180°﹣∠AFE,∴∠AFE=120°,
∴∠AEF=180°﹣120°﹣30°=30°;
如图2,设与AB交于点H,
若时,∴∠BCA=∠FHA=90°,
∴∠AFH=180°﹣∠AHF﹣∠A=180°﹣90°﹣30°=60°,
∵将△AEF沿着EF折叠,∴;
∴∠AEF=180°﹣∠A﹣∠AFE=120°;
如图3,
若时,∴,∴,
∵将△AEF沿着EF折叠,∴;
综上所述:30°或75°或120°.
【模型演练】
1.一条两边沿互相平行的围巾按图甲所示折叠并将其绘制成图乙,已知,且,则( )
A. B. C. D.
2.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB、CD,若CDBE,∠1=42°,则∠2的度数是( )
A.48° B.45° C.96° D.40°
3.如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2 B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2 D.在图4中,展开后测得∠1+∠2=180°
4.如图,将一张对边互相平行的纸条沿EF折叠,若∠EFB=32°,则①;②∠AEC=148°;③∠BGE=64°;④∠BFD=116°,则下列结论正确的有( )
A.1个 B.2个 C.3个 D.4个
5.为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④.其中能够判定两条边线、互相平行的个数是( )
A.1 B.2 C.3 D.4
6.如图,将一条两边沿互相平行的纸带折叠.则与的关系式是( )
A. B.
C. D.
7.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,且,则的度数是______.
8.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为和.若,,则的度数为______.
9.如图是我们常用的折叠式小刀,刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成∠1与∠2.若∠1=68°,则∠2=_______°.
10.在“妙折生平——折纸与平行”的拓展课上,小潘老师布置了一个任务:如图,有一张三角形纸片ABC,∠B=32°,∠C=60°,点D是AB边上的固定点(BD<AB),请在BC上找一点E,将纸片沿DE折叠(DE为折痕),点B落在点F处,使EF与三角形ABC的一边平行,则∠BDE为____________度.
11.如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部的位置,且与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=34°.若保持△DE的一边与BC平行,则∠ADE的度数____.
12.如图,将一条两边互相平行的纸带按图折叠,则α的度数等于______.
13.如图,在△ABC中,∠A=56°,∠C=46°,D是线段AC上一个动点,连接BD,把△BCD沿BD折叠,点C落在同一平面内的点处,当平行于△ABC边时,∠CDB的大小为______.
14.将一条两边互相平行的纸带沿EF折叠,如图(1),AD∥BC,ED'∥FC',设∠AED'=x°
(1)∠EFB=_____.(用含x的代数式表示)
(2)若将图1继续沿BF折叠成图(2),∠EFC″=_____.(用含x的代数式表示).
15.如图所示,将三角形纸片ABC沿DE折叠,使点B落在点B′处,若EB′恰好与BC平行,且∠B=80°,则∠CDE=_____°.
16.如图,将一张上、下两边平行(即ABCD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2;
(2)已知∠2=54°,求∠BEF的度数.
17.如图,把长方形ABCD的两角折叠,折痕分别为EF、HG,点B、D折叠后的对应点分别是、,并且使与在同一直线上,已知长方形的两组对边分别平行,试说明两条折痕EF、GH也相互平行.
18.有一条纸带ABCD,现小强对纸带进行了下列操作:
(1)为了检验纸带的两条边线AB与CD是否平行,小强如图①所示画了直线后,量得∠1=∠2,则,理由为 ;
(2)将这条上下两边互相平行的纸带折叠,如图②所示,设∠1为70°,请求出∠的度数;
(3)如图③,已知这是一条长方形纸带,点E在折线AD→DC上运动,点F是AB上的动点,连接EF将纸带沿着EF折叠,使点A的对应点落在DC上,若,请用含x的代数式来表示的度数为 .(直接写出答案)
19.综合与实践:折纸中的数学
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题,并进行了简单的计算与推理.七年级下册第五章我们学习了平行线的性质与判定,今天我们继续探究:折纸中的数学﹣﹣长方形纸条的折叠与平行线.
知识初探
(1)如图1,长方形纸条ABGH中,,∠A=∠B=∠G=∠H=,将长方形纸条沿直线CD折上,点A落在A'处,点B落在B'处,B'C交AH于点E,若∠ECG=,则∠CDE= ;
类比再探
(2)如图2,在图1的基础上将∠HEC对折,点H落在直线EC上的H'处,点G落在G'处得到折痕EF,则折痕EF与CD有怎样的位置关系?说明理由;
(3)如图3,在图2的基础上,过点G'作BG的平行线MN,请你猜想∠ECF和∠H'G'M的数量关系,并说明理由.
专题08 平行与折叠问题
【模型讲解】
如图,Rt△ABC中,∠C=90°,∠A=30°,E,F分别是边AC,AB上的点,连接EF,将△AEF沿EF折叠,得到,当的边与△ABC的一边平行时,∠AEF的度数是_____.
解:如图1,若时,∴,∵∠C=90°,∠A=30°,
∴,∵将△AEF沿EF折叠,得到,
∴,∴∠BFE=180°﹣∠AFE,
∴∠AFE﹣60°=180°﹣∠AFE,∴∠AFE=120°,
∴∠AEF=180°﹣120°﹣30°=30°;
如图2,设与AB交于点H,
若时,∴∠BCA=∠FHA=90°,
∴∠AFH=180°﹣∠AHF﹣∠A=180°﹣90°﹣30°=60°,
∵将△AEF沿着EF折叠,∴;
∴∠AEF=180°﹣∠A﹣∠AFE=120°;
如图3,
若时,∴,∴,
∵将△AEF沿着EF折叠,∴;
综上所述:30°或75°或120°.
【模型演练】
1.一条两边沿互相平行的围巾按图甲所示折叠并将其绘制成图乙,已知,且,则( )
A. B. C. D.
【答案】D
【分析】将围巾展开,根据折叠的性质得:则∠ADM=∠ADF,∠KCB=∠BCN,设∠ABC=x,根据平行线的性质得:∠FDC=∠KCG=2x,由平角的定义列式:∠FDC+∠FDM=180°,可得x的值,从而得结论.
【详解】解:如图乙,将围巾展开,则∠ADM=∠ADF,∠KCB=∠BCN,
设∠ABC=x,则∠DAB=x+20°,
∵CDAB,
∴∠ADM=∠DAB=x+20°=∠ADF,
∵DFCG,
∴∠FDC=∠KCG=2x,
∵∠FDC+∠FDM=180°,
∴2x+2(x+20°)=180°,
解得:x=35°,
∴3∠DAB+∠ABC=3(x+20°)+x=4x+60°=200°,
故选:D.
【点睛】此题考查了平行线性质,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
2.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB、CD,若CDBE,∠1=42°,则∠2的度数是( )
A.48° B.45° C.96° D.40°
【答案】C
【分析】根据平行线的性质和折叠性质即可求解.
【详解】解:如图,
∵AGBE,ADBC,
∴∠1=∠5,∠5=∠4
∴∠4=∠1=42°,
∵CDBE,
∴∠4=∠3=42°,
由折叠性质得:∠6=∠3=42°,又∠6+∠3+∠2=180°,
∴∠2=96°.
故选:C.
【点睛】本题考查了平行线的性质、折叠的问题,解题的关键是熟练掌握平行线的性质定理.
3.如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2 B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2 D.在图4中,展开后测得∠1+∠2=180°
【答案】C
【分析】根据平行线的判定定理,进行分析,即可解答.
【详解】A、 当∠1=∠2时,内错角相等,两直线平行,所以;
B、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90∘,所以;
C、∠1=∠2不能判定a,b互相平行;
D、∠1+∠2=180°时,同旁内角互补,两直线平行,所以.
故选:C.
【点睛】本题考查平行线的判定,掌握平行线的判定定理是解题的关键.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
4.如图,将一张对边互相平行的纸条沿EF折叠,若∠EFB=32°,则①;②∠AEC=148°;③∠BGE=64°;④∠BFD=116°,则下列结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】根据平行线的性质及翻折变换的性质对各小题进行逐一分析即可.
【详解】解:①∵AEBG,∠EFB=32°,
∴=∠EFB=32°,故本小题正确;
②∵AEBG,∠EFB=32°,
∴∠AEF=180°-∠EFB=180°-32°=148°,
∵∠AEF=∠AEC+∠GEF,
∴∠AEC<148°,故本小题错误;
③∵=32°,
∴∠GEF==32°,
∴=+∠GEF=32°+32°=64°,
∵AEBG,
∴∠BGE==64°,故本小题正确;
④∵∠BGE=64°,
∴∠CGF=∠BGE=64°,
∵DFCG,
∴∠BFD=180°-∠CGF=180°-64°=116°,故本小题正确.
综上,①③④正确,共3个.
故选:C.
【点睛】本题考查的是平行线的性质及翻折变换的性质,熟知图形翻折不变性的性质是解答此题的关键.
5.为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④.其中能够判定两条边线、互相平行的个数是( )
A.1 B.2 C.3 D.4
【答案】B
【分析】由内错角相等,两直线平行可判断①,由等腰三角形的性质可得但是不能判定平行,可判断②,由等腰三角形的性质可得再结合轴对称的性质可得可判断③,由轴对称的性质可得但不能判定平行,从而可得答案.
【详解】解:
∴ 故①符合题意;
∵
∴ 不能得到 故②不符合题意;
∵
∴
由折叠可得:
∴
∴,故③符合题意;
∴ 不能得到 故④不符合题意;
故选B
【点睛】本题考查的是轴对称的性质,等腰三角形的性质,平行线的判定,掌握“轴对称的性质与等腰三角形的性质及平行线的判定方法”是解本题的关键.
6.如图,将一条两边沿互相平行的纸带折叠.则与的关系式是( )
A. B.
C. D.
【答案】C
【分析】根据折叠性质,先得出,根据,得出,,得出,根据,得出,即可得出结论.
【详解】解:根据折叠可知,,
∵,
,,
∴,
∵,
,即,故C正确.
故选:C.
【点睛】本题主要考查了平行线的性质,折叠的性质,根据题意得出,是解题的关键.
7.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,且,则的度数是______.
【答案】57°##57度
【分析】利用平行线的性质以及翻折不变性即可得到,再根据同旁内角互补可得,进而得出.
【详解】解:如图,延长到点,
纸带对边互相平行,
,
由折叠得,,
∵,
,
,
,
,即,
.
故答案为:.
【点睛】本题主要考查了平行线的性质,图形的折叠,熟练掌握平行线的性质,图形的折叠的性质是解题的关键.
8.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为和.若,,则的度数为______.
【答案】68°##68度
【分析】利用平行线的性质以及翻折不变性即可得到,进而得出,再由折叠的性质得.
【详解】解:如图,延长到点,
由折叠可得, ,
∵,
∴,
纸带对边互相平行,
∴,
∴,
由折叠可得,,
故答案为:.
【点睛】本题考查平行线的判定和性质,折叠的性质,解题的关键是熟练掌握:两直线平行,同位角相等;两直线平行,同旁内角互补.
9.如图是我们常用的折叠式小刀,刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成∠1与∠2.若∠1=68°,则∠2=_______°.
【答案】22°##22度
【分析】延长CE,交AD与点F,根据平行的性质有∠2=∠DFE,再根据∠1+∠DFE=90°,即可求出∠DFE,则问题得解.
【详解】延长CE,交AD与点F,如图,
根据题意有:,∠DEC=90°,
∴∠2=∠DFE,∠DEF=∠DEC=90°,
∴△DEF是直角三角形,即∠1+∠DFE=90°,
∵∠1=68°,
∴∠DFE=90°-∠1=22°,
∴∠2=22°,
故答案为:22°.
【点睛】本题考查了由平行线的性质探究角的关系;掌握两直线平行内错角相等是解题关键.
10.在“妙折生平——折纸与平行”的拓展课上,小潘老师布置了一个任务:如图,有一张三角形纸片ABC,∠B=32°,∠C=60°,点D是AB边上的固定点(BD<AB),请在BC上找一点E,将纸片沿DE折叠(DE为折痕),点B落在点F处,使EF与三角形ABC的一边平行,则∠BDE为____________度.
【答案】28°或74°或118°
【分析】分三种情况,分别画出图形,结合平行线的性质和三角形内角和定理,三角形外角的性质,即可求解.
【详解】解:当时,
由折叠得,∠B=∠F=32°,∠BED=∠DEF,
∵,
∴∠B=∠CEF=32°,
∴∠BEF=180°-32°=148°,
∴;
当时,
∵,
∴∠BEF=∠C=60°,
∴,
∴;
当时,
∴∠CEF=∠C=60°,
∴∠BGD=∠CEF+∠F=92°,
∴∠BDG=180°-∠B-∠BGD=56°,
∴;
综上所述,∠BDE为28°或74°或118°.
故答案为:28°或74°或118°
【点睛】本题主要考查了图形的折叠,平行线的性质,三角形外角的性质,三角形的内角和定理,熟练掌握平行线的性质,三角形外角的性质,三角形的内角和定理,利用分类讨论思想解答是解题的关键.
11.如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部的位置,且与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=34°.若保持△DE的一边与BC平行,则∠ADE的度数____.
【答案】45°或28°
【分析】根据题意,分,两种情况分析,根据平行线的性质与三角形的内角和定理即可求解.
【详解】解:∵将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部A'的位置,
∴当时,经过折叠在上,不符题意,
依题意,,
①当,
②当时,
故答案为:45°或28°
【点睛】本题考查了平行线的性质,折叠的性质,掌握三角形的外角的性质,内角和定理,平行线的性质是解题的关键.
12.如图,将一条两边互相平行的纸带按图折叠,则α的度数等于______.
【答案】75°##75度
【分析】由平行线的性质可知∠2=∠1,由折叠的性质可知2α+30=180,列方程求解.
【详解】解:∵ADBC,
∴∠2=∠1=30°,
∴2α+30=180,
∴α=75,
故答案为:75°.
【点睛】本题考查了折叠的性质,平行线的性质.根据折叠性质及互补关系列出方程是解题的关键.
13.如图,在△ABC中,∠A=56°,∠C=46°,D是线段AC上一个动点,连接BD,把△BCD沿BD折叠,点C落在同一平面内的点处,当平行于△ABC边时,∠CDB的大小为______.
【答案】或
【分析】先根据折叠的性质可得,设,再分①和两种情况,画出相应的图形,利用平行线的性质、平角的定义建立方程,解方程即可得.
【详解】解:由折叠的性质得:,
设,
由题意,分以下两种情况:
①如图,当时,
,
,
,
,
解得,
即;
②如图,当时,
,
,
,
解得,
即;
综上,的大小为或,
故答案为:或.
【点睛】本题考查了折叠的性质、平行线的性质、一元一次方程的应用,正确分两种情况,并画出图形是解题关键.
14.将一条两边互相平行的纸带沿EF折叠,如图(1),AD∥BC,ED'∥FC',设∠AED'=x°
(1)∠EFB=_____.(用含x的代数式表示)
(2)若将图1继续沿BF折叠成图(2),∠EFC″=_____.(用含x的代数式表示).
【答案】 90°- x° x°-90°
【分析】(1)由平行线的性质得∠DEF=∠EFB,∠AEH+∠EHB=180°,折叠和三角形的外角得∠D'EF=∠EFB,∠EFB=∠EHB,最后计算出∠EFB=90°- x°;
(2)由折叠和平角的定义求出∠EFC'=90°+ x°,再次折叠经计算求出∠EFC"= x°-90°.
【详解】解:(1)如图1所示,
∵AD∥BC,
∴∠DEF=∠EFB,∠AEH+∠EHB=180°,
又∵∠DEF=∠D'EF,
∴∠D'EF=∠EFB,
又∵∠EHB=∠D'EF+∠EFB,
∴∠EFB=∠EHB,
又∵∠AED'=x°,
∴∠EHB=180°-x°
∴∠EFB=(180°-2)=90°- x°
故答案为:90°- x°;
(2)如图2所示,
∵∠EFB+∠EFC'=180°,
∴∠EFC=∠EFC'=180°-(90°- x°)=90°+ x°,
又∵∠EFC'=2∠EFB+∠EFC",
∴∠EFC"=∠EFC'-2∠EFB=90°+ x°-2(90°- x°)
= x°-90°,
故答案为: x°-90°.
【点睛】本题综合考查了平行线的性质,折叠问题,等腰三角形的性质,三角形的外角定理,平角的定义以及角的和差等相关知识,重点掌握平行线的性质,难点是折叠前后的变及不变的问题,二次折叠角的前后大小等量关系.
15.如图所示,将三角形纸片ABC沿DE折叠,使点B落在点B′处,若EB′恰好与BC平行,且∠B=80°,则∠CDE=_____°.
【答案】130
【分析】先求出∠B=∠B′=80°,∠BDE=∠B′DE,根据平行线的性质得到∠B′DC=80°,进而得到∠BD B′=100°,∠BDE=50°,即可求出∠CDE=130°.
【详解】解:由折叠的定义得∠B=∠B′=80°,∠BDE=∠B′DE,
∵EB′∥BC,
∴∠B′=∠B′DC=80°,
∴∠BD B′=180°-∠B′DC=100°,
∴∠BDE=∠B′DE=50°,
∴∠CDE=180°-∠BDE=130°.
故答案为:130
【点睛】本题考查了折叠的定义,平行线的性质,邻补角的定义等知识,熟知相关知识并根据图形灵活应用是解题关键.
16.如图,将一张上、下两边平行(即ABCD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2;
(2)已知∠2=54°,求∠BEF的度数.
【答案】(1)见解析
(2)
【分析】(1)连续两次利用定理“两直线平行,内错角相等”即可求证;
(2)先利用求出,再利用求出,最后利用关系式求解即可.
(1)
解:证明:∵,
∴.
∵,
∴,
∴.
(2)
∵,∠2=54°
∴.
根据折叠的性质知:,
∴.
又∵,即,
∴,
∴.
【点睛】本题考查平行的性质,折叠的性质,掌握平行的性质和折叠前后对应的角相等是解题的关键.
17.如图,把长方形ABCD的两角折叠,折痕分别为EF、HG,点B、D折叠后的对应点分别是、,并且使与在同一直线上,已知长方形的两组对边分别平行,试说明两条折痕EF、GH也相互平行.
【答案】见解析
【分析】先根据折叠得出,,再根据平行线的性质得出,即可得出,最后根据平行线的判定得出结论.
【详解】证明:根据折叠可知,,,
∵长方形的两组对边分别平行,即
∴,
∵,,
∴,
∴.
【点睛】本题主要考查了平行线的判定和性质,折叠的性质,熟练掌握两直线平行,内错角相等和内错角相等两直线平行,是解题的关键.
18.有一条纸带ABCD,现小强对纸带进行了下列操作:
(1)为了检验纸带的两条边线AB与CD是否平行,小强如图①所示画了直线后,量得∠1=∠2,则,理由为 ;
(2)将这条上下两边互相平行的纸带折叠,如图②所示,设∠1为70°,请求出∠的度数;
(3)如图③,已知这是一条长方形纸带,点E在折线AD→DC上运动,点F是AB上的动点,连接EF将纸带沿着EF折叠,使点A的对应点落在DC上,若,请用含x的代数式来表示的度数为 .(直接写出答案)
【答案】(1)同位角相等,两直线平行
(2)
(3)或
【分析】(1)根据平行线的判定方法即可解决问题;
(2)如图②−1中,证明∠α=∠4即可解决问题;
(3)分两种情形:如图③−1中,证明∠DEA′=2∠EAA′,∠DEA′=∠CA′F即可;如图③−2中,证明∠EA′F=2∠EAA′即可解决问题.
(1)
解:如图①中,∵∠1=∠2,
∴(同位角相等两直线平行),
故答案为:同位角相等,两直线平行;
(2)
解:如图②−1中,
由翻折的性质可知,∠3=∠4,
∵,
∴∠α=∠3,
∴∠α=∠4,
∵∠1=∠2=70°,
∴;
(3)
解:如图③−1中,
由翻折可知,EA=EA′,∠EA′F=∠DAB=90°,
∴∠EAA′=∠EA′A,
∴∠DEA′=∠EAA′+∠EA′A=2∠EAA′,
∵四边形ABCD是矩形,
∴∠D=90°,
∵∠DEA′+∠DA′E=90°,∠DA′E+∠CA′F=90°,
∴∠DEA′=∠CA′F,
∴∠CA′F=2∠DAA′,
∴;
如图③−2中,
由翻折可知,EA=EA′,FA=FA′,
∴∠EAA′=∠EA′A,∠FAA′=∠FA′A,
∵,
∴∠EA′A=∠FAA′,
∴∠EAA′=∠AA′F,
∴∠EA′F=2∠EAA′,
∵∠CA′F+∠EA′F=180°,
∴2∠EAA′=180°−x,
∴,
故答案为:或.
【点睛】本题考查了平行线的性质,矩形的性质,三角形内角和定理及外角的性质,翻折变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.
19.综合与实践:折纸中的数学
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题,并进行了简单的计算与推理.七年级下册第五章我们学习了平行线的性质与判定,今天我们继续探究:折纸中的数学﹣﹣长方形纸条的折叠与平行线.
知识初探
(1)如图1,长方形纸条ABGH中,,∠A=∠B=∠G=∠H=,将长方形纸条沿直线CD折上,点A落在A'处,点B落在B'处,B'C交AH于点E,若∠ECG=,则∠CDE= ;
类比再探
(2)如图2,在图1的基础上将∠HEC对折,点H落在直线EC上的H'处,点G落在G'处得到折痕EF,则折痕EF与CD有怎样的位置关系?说明理由;
(3)如图3,在图2的基础上,过点G'作BG的平行线MN,请你猜想∠ECF和∠H'G'M的数量关系,并说明理由.
【答案】(1)
(2),理由见解析
(3),理由见解析
【分析】(1)先根据折叠的性质可得,再根据平角的定义可得,然后根据平行线的性质即可得;
(2)先根据折叠的性质可得,,再根据平行线的性质可得,从而可得,然后根据平行线的判定即可得出结论;
(3)过点作于,先根据平行线的性质可得,再根据平行公理推论可得,根据平行线的性质可得,然后根据折叠的性质可得,从而可得,最后根据等量代换即可得出结论.
(1)
解:由折叠的性质得:,
,,
,
,
,
故答案为:.
(2)
解:,理由如下:
由折叠的性质得:,,
,
,
,
.
(3)
解:,理由如下:
如图,过点作于,
,
又,
,
,
由折叠的性质得:,
,
.
【点睛】本题考查了折叠的性质、平行线的判定与性质、平行公理推论等知识点,熟练掌握平行线的性质和折叠的性质是解题关键.
专题04 解题技巧专题:特殊平行四边形中折叠、旋转问题(5大考点)-八年级数学下册重难点专题提优训练(苏科版): 这是一份专题04 解题技巧专题:特殊平行四边形中折叠、旋转问题(5大考点)-八年级数学下册重难点专题提优训练(苏科版),文件包含专题04解题技巧专题特殊平行四边形中折叠旋转问题解析版重点突围docx、专题04解题技巧专题特殊平行四边形中折叠旋转问题原卷版重点突围docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
八年级上册1.4 全等三角形测试题: 这是一份八年级上册1.4 全等三角形测试题,文件包含专题03三角形折叠中的角度问题解析版docx、专题03三角形折叠中的角度问题原卷版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
七年级数学下册考点精练专题15 和幂运算有关的新定义问题: 这是一份七年级数学下册考点精练专题15 和幂运算有关的新定义问题,共25页。












