
3.3用图像表示的变量间关系寒假预习自测北师大版数学七年级下册
展开3.3用图像表示的变量间关系寒假预习自测北师大版数学七年级下册
限时:60分钟;满分:100分
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
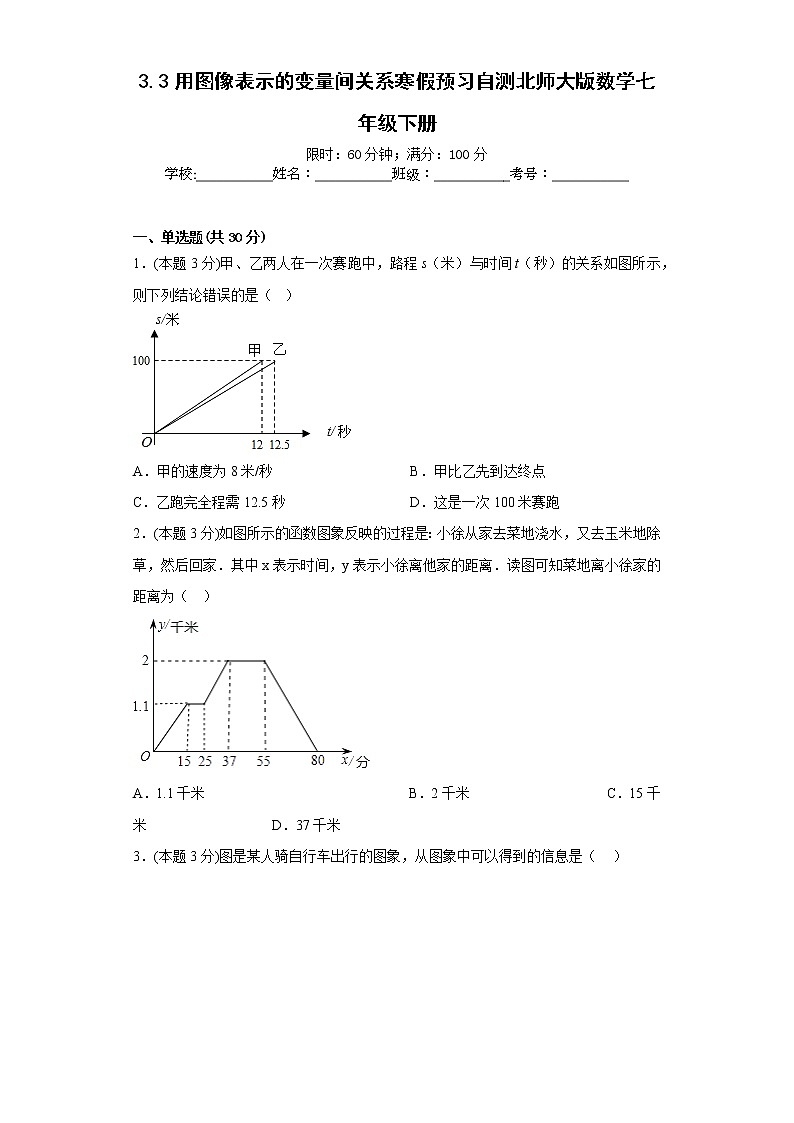
1.(本题3分)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示,则下列结论错误的是( )
A.甲的速度为8米/秒 B.甲比乙先到达终点
C.乙跑完全程需12.5秒 D.这是一次100米赛跑
2.(本题3分)如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
A.1.1千米 B.2千米 C.15千米 D.37千米
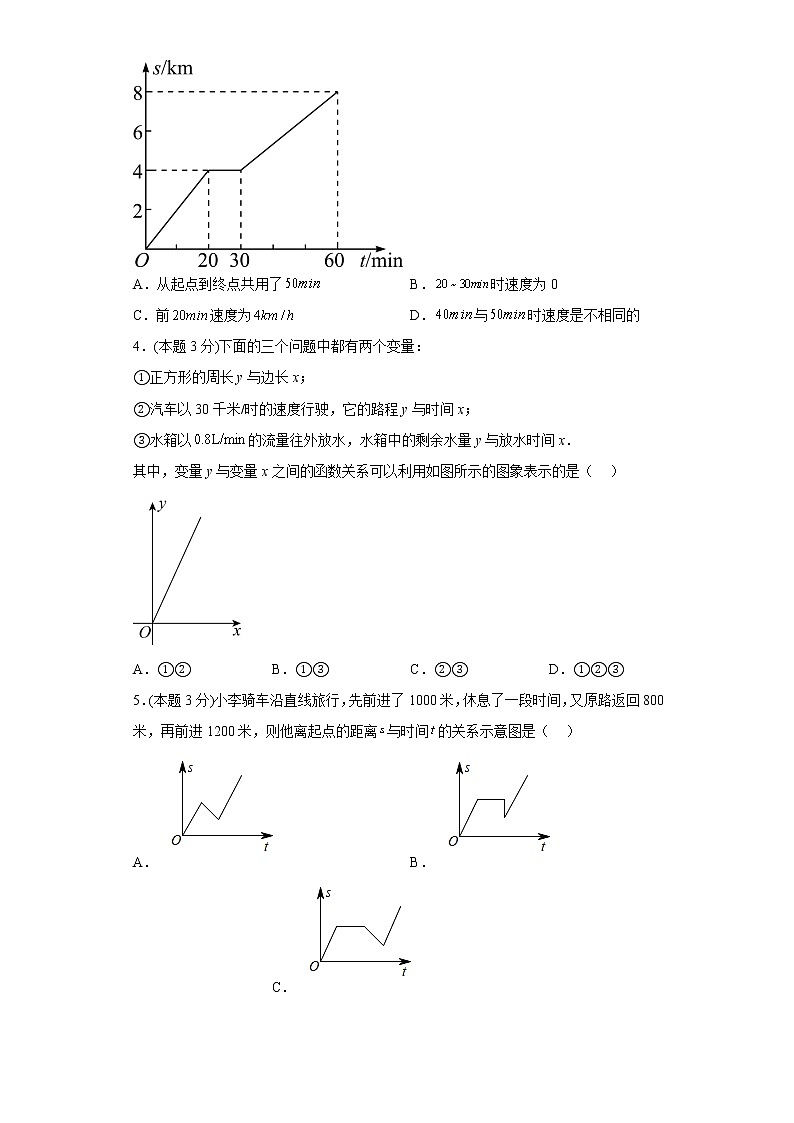
3.(本题3分)图是某人骑自行车出行的图象,从图象中可以得到的信息是( )
A.从起点到终点共用了 B.时速度为0
C.前速度为 D.与时速度是不相同的
4.(本题3分)下面的三个问题中都有两个变量:
①正方形的周长y与边长x;
②汽车以30千米/时的速度行驶,它的路程y与时间x;
③水箱以的流量往外放水,水箱中的剩余水量y与放水时间x.
其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )
A.①② B.①③ C.②③ D.①②③
5.(本题3分)小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离与时间的关系示意图是( )
A. B. C. D.
6.(本题3分)下列图象中,能反映出投篮时篮球的离地高度与投出后的时间之间关系的是( )
A. B.
C. D.
7.(本题3分)2013年“中国好声音”全国巡演重庆站在奥体中心举行,童童从家出发前往观看,先匀速步行至轻轨车站,等了一会儿,童童搭乘轻轨至奥体中心观看演出,演出结束后,童童搭乘邻居刘叔叔的车顺利回到家.其中x表示童童从家出发后所用的时间,y表示童童离家的距离.下面能反映y与x函数关系的大致图象是【 】
A. B. C. D.
8.(本题3分)已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A. B.
C. D.
9.(本题3分)如图,一只兔子和一只小狗从同一地点出发.下面说法正确的是( )
A.小狗的速度始终比兔子快
B.整个过程中,小狗和兔子的平均速度相同
C.在前3秒内,小狗比兔子跑得快
10.(本题3分)小明从家骑自行车上学,先以0.4千米/分的速度匀速骑行5分钟,途经超市时,买文具用了5分钟,为按时到校,再以0.5千米/分的速度骑行2分钟到学校.设小明骑自行车的速度为v(千米/分),离家路程为s(千米),上学时间为t(分).下列图象能表达这一过程的是( )
A. B. C. D.
二、填空题(共30分)
11.(本题3分)如图所示的程序是一种数值转换程序,当输入的x值为1.5时,输出的y值为________.
12.(本题3分)甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,根据图象回答:这是一次____米赛跑;先到达终点的是____;乙的速度是________.
13.(本题3分)把一个函数的自变量与对应的函数的值分别作为点的___坐标和___坐标,在直角坐标系中描出它的对应点,___的图形叫做这个函数的图象.
14.(本题3分)某物流公司的快递车和货车每天沿同一条路线往返于A、B两地,快递车比货车多往返一趟.如图所示,表示货车距离A地的路程y(单位:km)与所用时间x(单位h)的图像,其间在B地装卸货物2h.已知快递车比货车早1h出发,最后一次返回A地比货车晚1h.若快递车往返途中速度不变,且在A、B两地均不停留,则两车在往返途中相遇的次数为________次.
15.(本题3分)如图表示的是某种摩托车的油箱中剩余量(升)与摩托车行驶路程(千米)之间的关系.由图象可知,摩托车最多装__升油,可供摩托车行驶___千米,每行驶100千米耗油___升.
16.(本题3分)图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.则体育场离张强家_____千米,张强在体育场锻炼了_____分钟,张强从早餐店回家的平均速度是_____千米/小时.
17.(本题3分)一港口受潮汐的影响,某天小时港内的水深大致如图,港口规定:为了保证航行安全,只有当船底与水底间的距离不少于米时,才能进出该港.一艘吃水深度(即船底与水面的距离)为米的轮船进出该港的时间最多为(单位:时) ______小时.
18.(本题3分)邓教师设计一个计算程序,输入和输出的数据如表所示,当输入数据是正整数n时,输出的数据是________.
输入数据
1
2
3
4
5
6
……
输出数据
……
19.(本题3分)为了增强抗旱能力,保证今年夏粮丰收,某村新建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是________ .
20.(本题3分)如图1,在△ABC中,点P从点A出发向点C运动,在运动过程中,设x表示线段AP的长,y表示线段BP的长,y与x之间的关系如图2所示,当线段BP最短时,△BCP与△ABP的周长的差为__________。
三、解答题(共40分)
21.(本题8分)2022年3月31日云岭高速公路又添一大动脉——新楚大高速公路(楚雄到大理),成为了带动滇西经济发展的新干线,小杰爸爸带家人外出旅行,驾车途经新楚大高速公路时,小杰记录了汽车仪表盘上显示的数据,并制成如图:
(1)这辆汽车在高速公路上行驶的路程和耗油量成_____关系;
(2)行驶100千米耗油_____升,2升油可行驶_____千米;
(3)若这辆汽车油箱里剩余20升油,那么汽车还能行驶300千米吗?请说明理由.
22.(本题8分)如图①所示, 在△ABC中,AD是三角形的高,且AD=6 cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②所示,已知BC=8 cm.
(1)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;
(2)当E点停止后,求△ABE的面积.
23.(本题8分)如图是小李骑自行车离家的距离s (km)与时间t (h) 之间的关系.
(1)在这个变化过程中自变量__________,因变量是__________,
(2)小李__________时到达离家最远的地方?此时离家________km;
(3)分别写出在1<t<2时和2<t<4时小李骑自行车的速度为______ km/h 和______km/h.
(4)小李______时与家相距20km.
24.(本题8分)如图所示,是反映了爷爷每天晚饭后从家中出发去散步的时间与距离之间的关系的一幅图.
(1)下图反映了哪两个变量之间的关系?
(2)爷爷从家里出发后分钟到分钟可能在做什么?
(3)爷爷每天散步多长时间?
(4)爷爷散步时最远离家多少米?
(5)分别计算爷爷离开家后的分钟内、分钟内、分钟内的平均速度.
25.(本题8分)某种车的油箱加满油后,油箱中的剩余油量y(升)与车行驶路程x(千米)之间的关系,如图所示,根据图象回答下列问题:
(1)这种车的油箱最多能装 升油.
(2)加满油后可供该车行驶 千米.
(3)该车每行驶200千米消耗汽油 升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶 千米后,车辆将自动报警?
参考答案:
1.A
【分析】利用图象可得出,甲,乙的速度,以及所行路程等,注意利用所给数据结合图形逐个分析.
【详解】解:结合图象可知:s=100m,甲比乙先到达终点,乙跑完全程需12.5秒,
故B、C、D说法正确;
甲的速度是100÷12≈8.3(米/秒),故A说法不正确;
故选:A.
【点睛】此题考查了利用图象得出正确信息,解题的关键是能从图中获取相应的信息.
2.A
【详解】解:由图象可以看出菜地离小徐家1.1千米.故选A.
点睛:本题考查了利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义是解题的关键.
3.B
【分析】分别根据函数图象的实际意义可依次判断各个选项是否正确.
【详解】、从起点到终点共用了,故本选项错误;
、时速度为0,故本选项正确;
、前的速度是,故本选项错误;
、与时速度是相同的,故本选项错误.
故选:.
【点睛】本题考查了函数图象的读图能力.要理解函数图象所代表的实际意义是什么才能从中获取准确的信息.
4.A
【分析】①根据正方形的周长公式判断即可;②根据“路程速度时间”判断即可;③根据“水箱中的剩余水量水箱的水量”判断即可.
【详解】解:正方形的周长与边长的关系式为,故①符合题意;
汽车以30千米时的速度行驶,它的路程与时间的关系式为,故②符合题意;
水箱以的流量往外放水,水箱中的剩余水量与放水时间关系式为:水箱中的剩余水量水箱的水量,故③不符合题意;
所以变量与变量之间的函数关系可以用如图所示的图象表示的是①②.
故选:A.
【点睛】本题考查了利用函数的图象解决实际问题,正确理解函数图象表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
5.C
【分析】根据休息时,离开起点的S不变,返回时S变小,再前进时S逐渐变大得出函数图象,然后选择即可.
【详解】解:前进了1000米图象为一条线段,
休息了一段时间,离开起点的不变,
又原路返回800米,离开起点的变小,
再前进1200米,离开起点的逐渐变大,
纵观各选项图象,只有选项符合.
故选:.
【点睛】本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
6.C
【分析】根据题意,篮球离地高度与投出时间的关系的图象为抛物线,然后选择即可.
【详解】投篮时篮球的离地高度与投出后的时间之间关系的函数图象为抛物线,
能够反映出投篮时篮球的离地高度与投出后的时间之间关系的是选项的图象.
故选:.
【点睛】本题考查了函数图象,主要是对抛物线的理解与抛物线图象的认识,是基础题.
7.A
【详解】童童先匀速步行至轻轨车站,图象平缓向上;
等了一会儿,图象平行于横轴;
搭乘轻轨至奥体中心,图象比步行陡一些向上;
观看演出,图象平行于横轴;
演出结束搭乘邻居刘叔叔的车回到家,图象向下.
综上所述,函数图象分为五段:平缓向上-平-陡些向上-平-向下.故选A.
8.B
【分析】根据题意求出2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,进而根据相遇前、相遇后两个阶段得出相应的分段函数,从而找出符合题意的图象.
【详解】解:根据题意,两人同时相向出发,甲到达B地时间为:=6小时,乙到达A地:=3小时.
根据题意,分成两个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地;
相遇前,s=120﹣(20+40)t=120﹣60t(0≤t≤2),当两者相遇时,t=2,s=0,
相遇后,当乙到达A地前,甲乙均在行驶,即s=(20+40)(t﹣2)=60t﹣120(2≤t≤3),当乙到达A地时,此时两者相距60千米;
当乙到达A地后,剩下甲在行驶,即s=60+20(t﹣3)=20t(3≤t≤6),
故:
故选B.
点评:此题主要考查了函数图象,根据题意得出关键转折点是解题关键.
9.B
【分析】由图可知:在前3秒内,小狗比兔子跑得慢,即可判定A、C,根据小狗与兔子同时出发,同时到达,即可判定B.
【详解】解:由图可知:在前3秒内,小狗比兔子跑得慢,故A、C错误;
由图可知:小狗与兔子同时出发,8分钟时都跑了8米,
故整个过程中,小狗和兔子的平均速度相同,故B正确,
故选:B.
【点睛】本题考查了利用图象解决问题,从图象中获取相关信息是解决本题的关键.
10.D
【分析】根据路程、速度与时间的关系以及函数图象的特点,结合题意逐项判断解答即可.
【详解】解:由题意,小明先以0.4千米/分的速度匀速骑行5分钟,路程从0 开始随时间匀速增加到2千米;
途经超市时,买文具用了5分钟,路程不变;
再以0.5千米/分的速度骑行2分钟到学校,离家路程随时间匀速增加到3千米.
故选:D.
【点睛】本题考查用图象表示变量间关系,理解题意,能判断出路程与时间的关系是解答的关键,注意买文具时路程不变.
11.0.5
【分析】先根据x的取值确定x的范围,从而得出需要代入的函数关系式,然后代入计算即可.
【详解】解:因为x=1.5满足:,所以把x=1.5代入,得:.
故答案为:0.5.
【点睛】本题考查了用关系式表示变量之间的关系以及因变量的求值,属于常见题型,读懂题意、弄清需要代入的函数关系式是解题关键.
12. 100 甲 8米/秒
【详解】解:(1)由图可知,两人所跑路程最大值为100米,
∴这是一次100米赛跑;
(2)由图可知,甲先到达终点;
(3)由图可知,乙跑完100米用了12.5秒,
∴乙的速度为:100÷12.5=8(米/秒).
故答案为:(1) 100 (2)甲 (3) 8米/秒
13. 横 纵 由这些点组成
【分析】利用对于一个函数,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象,进而得出即可.
【详解】解:把一个函数的自变量与对应的函数的值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,
由这些点组成的图形叫做这个函数的图象.
故答案为:横,纵,由这些点组成.
【点睛】此题主要考查了函数图形的定义,熟练根据函数定义得出是解题关键.
14.2
【分析】根据图象可知货车往返A、B一趟需8小时,则快递车往返A、B一趟需5小时,依此画出图象,再观察其图象与货车图象相交的次数即可.
【详解】解:根据题意可知货车往返A、B一趟需8小时,则快递车往返A、B一趟需5小时,在图上作出快递车距离A地的路程y(单位:km)与所用时间x(单位:h)的图象,由图象可知:两车在往返途中相遇的次数为2次.
故答案为:2.
【点睛】本题考查了利用图象表示变量之间的关系,正确理解题意、画出快递车的函数图象是解题关键.
15. 10 500 2
【分析】根据图象可知,当x=0时,对应y的数值就是摩托车最多装多少升油,当y=0时,x的值就是摩托车行驶的千米数;根据摩托车油箱可储油10升,可以行驶500km即可得出每行驶100千米消耗汽油升数.
【详解】解:由图象可知,摩托车最多装10升油,可供摩托车行驶500千米,每行驶100千米耗油2升.
故答案为:10,500,2.
【点睛】此题主要考查了利用函数图象解决问题,从图象上获取正确的信息是解题关键.
16.
【分析】结合图象,可得出体育场离张强家的距离为第一段图象所对应的轴的最高点;进而得出在体育场锻炼的时间;根据图象,可得出早餐店离张强家为千米,所用时间为分钟,注意要将单位转化为小时,再根据“平均速度=总路程总时间”,即可得出结果.
【详解】解:由图象得:体育场离张强家的距离千米,张强在体育场锻炼的时间为:分钟,
∵早餐店离张强家为千米,
又∵张强从早餐店回家所用时间为:分钟,
即分钟=小时,
∴张强从早餐店回家的平均速度为:千米/小时.
故答案为:;;
【点睛】本题考查了用图象表示变量之间的关系,解本题的关键在充分利用数形结合思想.
17.
【分析】从图像上找到当水深为米的两个时间相减即可得到本题的答案.
【详解】解:当船底与水底间的距离不少于米时,才能进出该港.
水深度即船底与水面的距离为米的轮船在水深为米时才可以通航,
从图像可知水深为米的时间为时和时,
进出该港口的时间为小时,
故答案为:.
【点睛】本题考查了用图像表示变量之间的关系,解决本题的关键是理解吃水的概念.
18.
【分析】观察表格中的数据可得:各个式子的分子是输入的数字,分母是输入数字的3倍减1,据此解答即可.
【详解】解:因为各个式子的分子是输入的数字,分母是输入数字的3倍减1,所以当输入数据是正整数n时,输出的数据是:.
故答案为:.
【点睛】本题考查了利用表格表示变量之间的关系和数据规律的探求,分别找出式子的分子与分母的规律是解本题的关键.
19.③
【分析】根据图象1可知进水速度小于出水速度,结合图2中特殊点的实际意义即可作出判断.
【详解】解:图象1可知进水速度小于出水速度,两只进水管的进水量与一只出水管的出水量相同
可得:
①0点到1点既进水,也出水;
②1点到4点同时打开两个管进水,和一只管出水;
③4点到6点只进水,不出水.
正确的只有③.
20.5.5
【分析】由图2及题意可得、、及的长,当线段最短时,,此时由勾股定理可求得的长,从而可分别求得及的周长,最后可求得这两个三角形周长的差.
【详解】解: 从图2可以看出:
,
当线段最短时,,此时,,
的周长,
的周长,
故:与的周长的差为5.5,
故答案为:5.5.
【点睛】本题考查了垂线段最短,勾股定理,读懂y与x之间的关系图,进而得、、及的长是解题的关键.
21.(1)正比例;
(2)8,25;
(3)不能,理由见解析.
【分析】(1)根据函数的图像即可判断路程和耗油量的关系;
(2)观察图像即可得出结论;
(3)根据第(2)小题的答案汽车每行驶100千米的耗油量可算出汽车行驶300千米的耗油量,再与20升油作比较即可.
【详解】(1)解:这辆汽车在高速公路上行驶的路程和耗油量成正比例关系.
故答案为:正比例;
(2)由图可得,行驶100千米耗油8升,2升油可行驶25千米.
故答案为:8,25;
(3)不能.理由:
由图可得,行驶100千米需要8升油,那么行驶300千米需要24升油,现在邮箱还有20升油,所以不够行驶300千米.
【点睛】本题主要考查了变量之间的关系,能正确的读图,并且从图像中获取信息是解答本题的关键.
22.(1)y=9x(0<x≤2);(2)△ABE的面积是18cm2.
【分析】根据三角形的面积公式,可得答案.
【详解】(1)由图2可知E点的速度为3,
∴y=×3x×AD=9x,即y=9x(0<x≤2);
(2)当E点停止后,BE=6,
∴x=2时,y=9×2=18.
∴△ABE的面积是18cm2.
【点睛】本题考查了函数关系式,三角形的面积公式是解题关键.
23.(1)离家时间,离家距离;(2)2,30;(3)20,5;(4)h或4h.
【分析】(1)在坐标系中横坐标是自变量,纵坐标是因变量,据此求解;
(2)根据图象可以得到离家最远时的时间,此时离家的距离,据此即可确定;
(3)根据图象可以得到从1时开始到2时自行车移动的距离和所用的时间,从2时开始到4时自行车移动的距离和所用的时间,据此即可求得;
(4)根据图象可以得到有两个时间点,据此即可确定.
【详解】解:(1)在这个变化过程中自变量离家时间,因变量是离家距离,
故答案为:离家时间,离家距离;
(2)根据图象可知小李2h后到达离家最远的地方,此时离家30km,
故答案为:2,30;
(3)当1≤t≤2时,小李行进的距离为30-10=20(km),用时2-1=1(h),
所以小李在这段时间的速度为:(km/h),
当2≤t≤4时,小李行进的距离为30-20=10(km),用时4-2=2(h),
所以小李在这段时间的速度为:(km/h),
故答案为:20,5;
(4)根据图象可知:小李h或4h与家相距20km,
故答案为:h或4h.
【点睛】本题考查了一次函数的图象,根据图象正确理解s随t的增大的变化情况是关键.
24.(1)爷爷散步的时间与距离之间的关系;(2)可能在某处休息;(3)爷爷每天散步45分钟;(4)爷爷散步时最远离家为900米;(5)爷爷离开家后:20分钟内平均速度是45米/分;30分钟内平均速度是30米/分;45分钟内平均速度是40米/分.
【分析】(1)根据图象中的横纵坐标的意义解答即可;
(2)根据图象可看出20分钟到30分钟之间,时间在增加,而路程不变,据此解答即可;
(3)根据图象可得45分钟后爷爷离家的距离为0,说明回到了家中,由此可得答案;
(4)图象最高点的纵坐标即为爷爷散步时最远离家的距离,据此即可解答;
(5)利用时间=路程÷速度求解即可.
【详解】解:(1)爷爷散步的时间与距离之间的关系;
(2)可能在某处休息.
(3)爷爷每天散步45分钟
(4)爷爷散步时最远离家为900米
(5)爷爷离开家后:①20分钟内平均速度:90020=45(米/分);
②30分钟内平均速度:90030=30(米/分);
③45分钟内平均速度:90045=40(米/分).
【点睛】本题考查了利用图象表示变量之间的关系,属于常考题型,正确理解图象的横纵坐标表示的意义是解题关键.
25.(1)50;(2)1000;(3)10;(4)800
【分析】(1)当x=0时,y的值就是这种车的油箱的最大容量;
(2)当y=0时,x的值就是该车行驶的行驶里程;
(3)观察图象可知,该车每行驶200千米消耗汽油10升;
(4)观察图象可知,行驶800千米后,车辆将自动报警.
【详解】解:(1)这种车的油箱最多能装50升油.
(2)加满油后可供该车行驶1000千米.
(3)该车每行驶200千米消耗汽油10升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶800千米后,车辆将自动报警.
故答案为:(1)50;(2)1000;(3)10;(4)800.
【点睛】此题主要考查了函数的图象,从一次函数的图象上获取正确的信息是解题关键.
初中3 用图象表示的变量间关系随堂练习题: 这是一份初中<a href="/sx/tb_c77852_t7/?tag_id=28" target="_blank">3 用图象表示的变量间关系随堂练习题</a>,共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
北师大版七年级下册3 用图象表示的变量间关系综合训练题: 这是一份北师大版七年级下册<a href="/sx/tb_c77852_t7/?tag_id=28" target="_blank">3 用图象表示的变量间关系综合训练题</a>,共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中北师大版3 用图象表示的变量间关系习题: 这是一份初中北师大版3 用图象表示的变量间关系习题,共13页。试卷主要包含了单选题,填空题,解答题,综合题等内容,欢迎下载使用。