2023届高考数学二轮复习2-1-7解析几何学案含答案

七　解析几何

『必记知识』

1．直线方程的五种形式

(1)点斜式：y－y1＝k(x－x1)(直线过点P1(x1，y1)，且斜率为k，不包括y轴和平行于y轴的直线)．

(2)斜截式：y＝kx＋b(b为直线l在y轴上的截距，且斜率为k，不包括y轴和平行于y轴的直线)．

(3)两点式：＝(直线过点P1(x1，y1)，P2(x2，y2)，且x1≠x2，y1≠y2，不包括坐标轴和平行于坐标轴的直线)．

(4)截距式：＝1(a，b分别为直线的横、纵截距，且a≠0，b≠0，不包括坐标轴、平行于坐标轴和过原点的直线)．

(5)一般式：Ax＋By＋C＝0(其中A，B不同时为0)．

2．直线的两种位置关系

当不重合的两条直线l1和l2的斜率存在时：

(1)两直线平行l1∥l2⇔k1＝k2.

(2)两直线垂直l1⊥l2⇔k1·k2＝－1.

3．三种距离公式

(1)A(x1，y1)，B(x2，y2)两点间的距离

|AB|＝.

(2)点到直线的距离d＝(其中点P(x0，y0)，直线方程为Ax＋By＋C＝0)．

(3)两平行线间的距离d＝(其中两平行线方程分别为l1：Ax＋By＋C1＝0，l2：Ax＋By＋C2＝0且C1≠C2)．

4．圆的方程的两种形式

(1)圆的标准方程：(x－a)2＋(y－b)2＝r2.

(2)圆的一般方程：

x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0)．

5．直线与圆、圆与圆的位置关系

(1)直线与圆的位置关系：相交、相切、相离，代数判断法与几何判断法．

(2)圆与圆的位置关系：相交、内切、外切、外离、内含，代数判断法与几何判断法．

6．椭圆的标准方程及几何性质

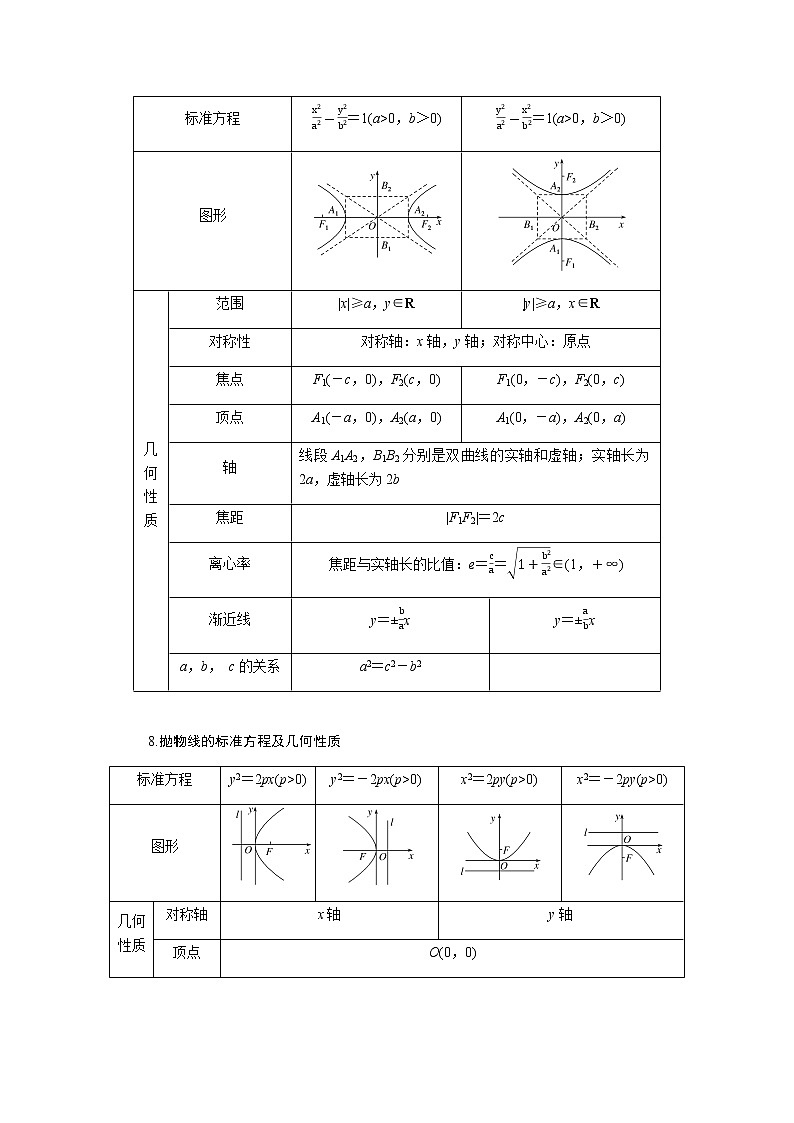
7.双曲线的标准方程及几何性质

8.抛物线的标准方程及几何性质

9.双曲线的方程与渐近线方程的关系

(1)若双曲线的方程为＝1(a>0，b>0)，则渐近线的方程为＝0，即y＝±x.

(2)若渐近线的方程为y＝±x(a>0，b>0)，即±＝0，则双曲线的方程可设为＝λ(λ≠0)．

(3)若所求双曲线与双曲线＝1(a>0，b>0)有公共渐近线，其方程可设为＝λ(λ>0，焦点在x轴上；λ<0，焦点在y轴上)．

10．抛物线焦点弦的相关结论

设AB是过抛物线y2＝2px(p>0)的焦点F的弦，若A(x1，y1)，B(x2，y2)，α为直线AB的倾斜角，则

(1)x1x2＝，y1y2＝－p2.

(2)弦长|AB|＝x1＋x2＋p＝.

(3)＝.

(4)以弦AB为直径的圆与准线相切．

【易错剖析】

易错点1　遗漏方程表示圆的充要条件

【突破点】　二元二次方程x2＋y2＋Dx＋Ey＋F＝0表示圆的充要条件是D2＋E2－4F>0，在此条件下，再根据其他条件求解．

易错点2　解决截距问题忽略“0”的情形

【突破点】　解决直线在两坐标轴上的截距或截距具有某种倍数关系的问题时，需注意两点：

(1)截距不是距离，直线在坐标轴上的截距可正、可负、也可为0.

(2)明确直线方程的截距式不能表示过原点或与坐标轴垂直的直线．因此解题时应该从截距是否为0进行分类讨论．

易错点3　忽视斜率不存在的情况

【突破点】　(1)在解决两直线平行的相关问题时，若利用l1∥l2⇔k1＝k2求解，忽略k1，k2不存在的情况，就会导致漏解．

(2)对于解决两直线垂直的相关问题时，若利用l1⊥l2⇔k1·k2＝－1求解，要注意其前提条件是k1与k2必须同时存在．

易错点4　忽略直线与圆锥曲线相交问题中的判别式

【突破点】　凡是涉及直线与圆锥曲线位置关系的问题，一定不能忘记对判别式的讨论．

易错点5　忽视双曲线定义中的条件

【突破点】　　双曲线的定义中，有两点是缺一不可的：其一，绝对值；其二，2a<|F1F2|.如果不满足第一个条件，动点到两定点的距离之差为常数，而不是差的绝对值为常数，那么其轨迹只能是双曲线的一支．

易错点6　忽视圆锥曲线定义中的焦点位置

【突破点】　椭圆的焦点位置由分母的大小确定，双曲线则是根据二次项系数的符号来确定的．解决此类问题时，一定要将方程化为曲线的标准形式．

【易错快攻】

易错快攻一　遗漏直线的斜率不存在的情况

[典例2]　[2022·全国乙卷]已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过A(0，－2)，B(，－1)两点．

(1)求E的方程；

(2)设过点P(1，－2)的直线交E于M，N两点，过M且平行于x轴的直线与线段AB交于点T，点H满足＝.证明：直线HN过定点．

听课笔记：

易错快攻二　忽视双曲线定义中的限制条件

[典例2]　点P到曲线E上所有点的距离的最小值称为点P到曲线E的距离，那么平面内到定圆C的距离与到圆C外的定点A的距离相等的点P的轨迹是(　　)

A．射线   B．椭圆

C．双曲线的一支 D．双曲线

听课笔记：

七　解析几何

[典例1]　解析：(1)设椭圆E的方程为mx2＋ny2＝1(m>0，n>0，m≠n)．

将点A(0，－2)，B(，－1)的坐标代入，得解得

所以椭圆E的方程为＝1.

(2)证明：方法一　设M(x1，y1)，N(x2，y2)．

由题意，知直线MN与y轴不垂直，设其方程为x－1＝t(y＋2)．

联立得方程组

消去x并整理，得(4t2＋3)y2＋(16t2＋8t)y＋16t2＋16t－8＝0，

所以y1＋y2＝－，y1y2＝.

设T(x0，y1)．由A，B，T三点共线，得＝，得x0＝y1＋3.

设H(x′，y′)．

由＝，得(y1＋3－x1，0)＝(x′－y1－3，y′－y1)，

所以x′＝3y1＋6－x1，y′＝y1，

所以直线HN的斜率k＝＝＝，

所以直线HN的方程为y－y2＝·(x－x2)．

令x＝0，得y＝·(－x2)＋y2

＝＋y2

＝

＝

＝－2.

所以直线NH过定点(0，－2)．

方法二　由A(0，－2)，B(，－1)可得直线AB的方程为y＝x－2.

a．若过点P(1，－2)的直线的斜率不存在，则其直线方程为x＝1.

将直线方程x＝1代入＝1，可得N(1，)，M(1，－)．

将y＝－代入y＝x－2，可得T(3－，－)．

由＝，得H(5－2，－)．

此时直线HN的方程为y＝(2＋)(x－1)＋，

则直线HN过定点(0，－2)．

b．若过点P(1，－2)的直线的斜率存在，设此直线方程为kx－y－(k＋2)＝0，M(x1，y1)，N(x2，y2)．

联立得方程组

消去y并整理，得(3k2＋4)x2－6k(2＋k)x＋3k(k＋4)＝0.

所以则

且x1y2＋x2y1＝.①

联立得方程组，可得T(＋3，y1)．

由＝，得H(3y1＋6－x1，y1)．

则直线HN的方程为y－y2＝(x－x2)．

将点(0，－2)的坐标代入并整理，得2(x1＋x2)－6(y1＋y2)＋x1y2＋x2y1－3y1y2－12＝0.②

将①代入②，得24k＋12k2＋96＋48k－24k－48－48k＋24k2－36k2－48＝0，显然成立．

综上可得，直线HN过定点(0，－2)．

[典例2]　解析：设圆C的半径为r，依据题意可知，|PC|＝|PA|＋r，即|PC|－|PA|＝r，且r<|AC|，

故所求点P的轨迹为以A，C为焦点的双曲线靠近A点的一支，故选C.

答案：C