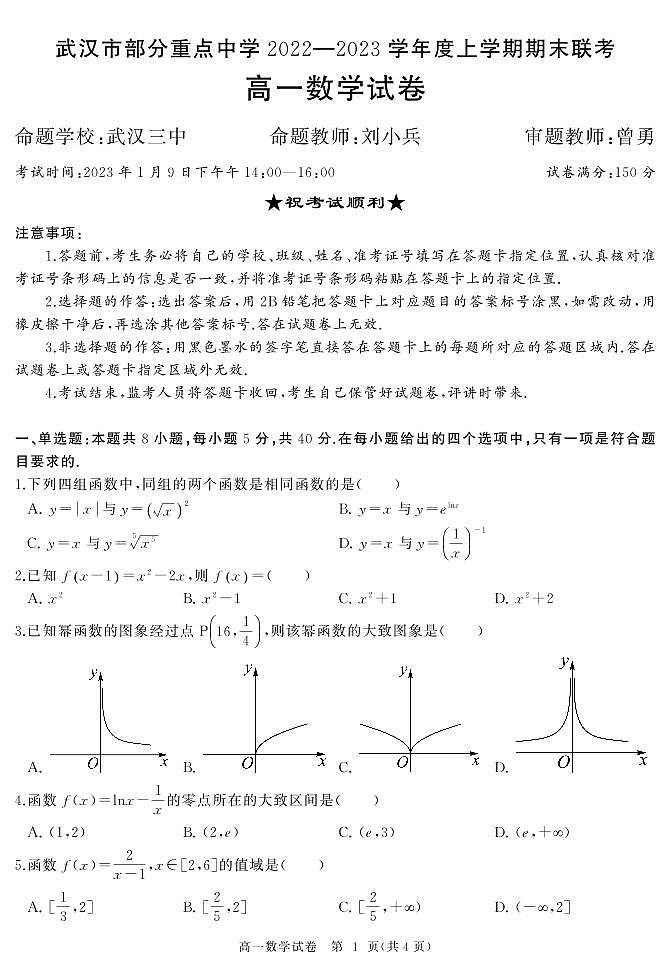
武汉市部分重点中学2022-2023学年度上学期期末联考高一数学试题

武汉市部分重点中学2022—2023学年度上学期期末联考

高一数学答案

一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

1. C   2.B   3. A   4.A   5.B   6.D   7.B

8. C【详解】特殊值法：函数与的图象上存在关于轴对称的点，则有解，注意到：，。只需考虑时，有解即可：

当，=有解即可，显然，所以成立.

当，时，由，无解，所以不成立，答案选C

二.多选题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有错选的得0分。

9.ABC   10.ABC    11.CD

12.ABD【详解】表示横坐标变为原来2倍的同时纵坐标标为原来的2倍。首先作出在上的图像,然后根据图像的变换作出在定义域上的图像，如图所示，由图可知，A,B都正确。因为则，由。

当且时，函数单调递减，所以D正确。

三.填空题：本题共4小题，每小题5分，共20分。

13.     14.6      15.

16..令,则对于一个确定的m值，关于x的方程最多两解；其中作出函数f(x)图像，

由图像可知：

,此时方程有两解；

,此时方程有三解；

,此时方程有四解；

,此时方程有七解；

,此时方程有八解；

,此时方程有六解；

,此时方程有四解；

四.解答题:共70分，解答应写出文字说明、证明过程或演算步骤。

17.【答案】（1）原式

（2）

18.【答案】（1）

（2）∵已知为第三象限角,，∴

,

19.【答案】：(1)由图可得:,由,得,故，

∵，即，则，

∴，则，又∵，则，故.

（2）根据题意：将函数的图象向左平移个单位，得到，

再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变）得到函数，

∵，则，即：直线与函数有两个不同的交点，

又当时，，递增，值域为:.

当时，，递减，值域为:

∴如果直线与函数有两个不同的交点，则：，

故的取值范围为:.

20.【答案】：（1）由图可知，当；，

又f（1）＝44.42，所以a+47.42＝44.42，解得a＝-12；

所以当。

（2）由题意知，当车辆驾驶人员血液中的酒精小于20毫克/百毫升时可以驾车，此时x＞2；

由＜20，得，两边取自然对数，得:，

即：﹣0.3x＜，解得：x＞＝5.7；

故喝啤酒后需5小时42分钟后才可以合法驾车．　

21.【答案】（1）当时，，因为,,当且仅当，即时取等，所以,所以函数的值域为.

（2），，使得，等价于，

令，，，令，则在上的最大值等于在上的最大值，因为在上单调递减，在上单调递增，所以在上的最大值为，所以，因此.

设，则，

任取，，

因为，所以，，，，，

所以，，所以在上为单调递增函数，

当时，函数在上为单调递减函数，

所以，所以，得；

当，函数在上为单调递增函数，

所以，所以，.

综上得：实数的取值范围为.

22.【答案】：（1）若不等式在x∈[]能成立，即在x∈[]能成立，即在x∈[]上能成立，令,知：值域为..

（2）设t=g(x)==-1+在x∈递减，可得t∈[1，4]，，

原问题转化为求实数a的取值范围，使得在t∈[1，4]上，恒有2ymin＞ymax．

讨论：

①当时，y=t+在[1，4]上递增，∴ymin=1+a，ymax=，

由2ymin＞ymax得；

②当时，y=t+在[1，]上单调递减，在[，4]上单调递增，且

∴ymin=2，ymax=，由2ymin＞ymax得，

∴；即

③当时，y=t+在[1，]上单调递减，在[，4]上单调递增，且， 

∴ymin=2，ymax=1+a，由2ymin＞ymax得+，

由于∴+；

④当时，y=t+在[1，4]单调递减，∴ymin=，ymax=1+a，

由2ymin＞ymax得；；

综上，a的取值范围是+).