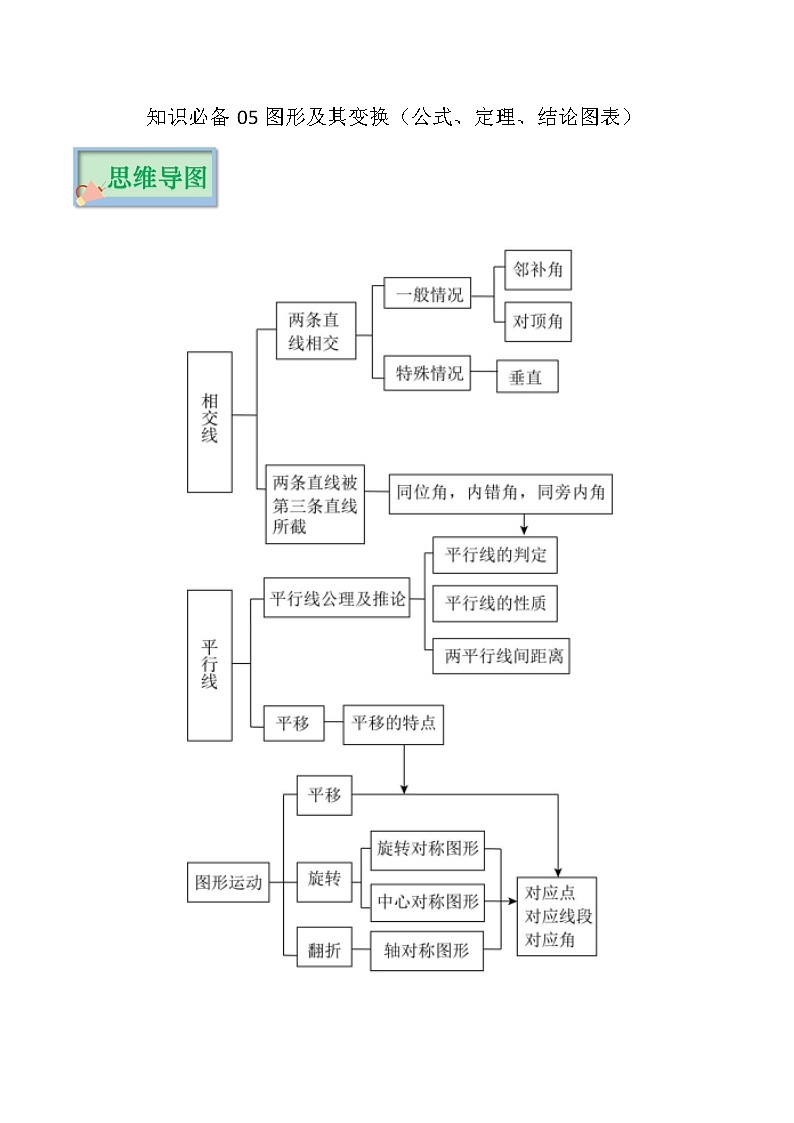


知识必备05 图形及其变换(公式、定理、结论图表)-2023年中考数学必背知识手册
展开知识必备05图形及其变换(公式、定理、结论图表)
考点一、平移变换
1. 平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.
【要点诠释】
(1)平移是运动的一种形式,是图形变换的一种,本讲的平移是指平面图形在同一平面内的变换;
(2)图形的平移有两个要素:一是图形平移的方向,二是图形平移的距离,这两个要素是图形平移的依据;
(3)图形的平移是指图形整体的平移,经过平移后的图形,与原图形相比,只改变了位置,而不改变图形的大小,这个特征是得出图形平移的基本性质的依据.
2.平移的基本性质:由平移的概念知,经过平移,图形上的每一个点都沿同一个方向移动相同的距离,平移不改变图形的形状和大小,因此平移具有下列性质:经过平移,对应点所连的线段平行且相等,对应角相等.
【要点诠释】
(1)要注意正确找出“对应线段,对应角”,从而正确表达基本性质的特征;
(2)“对应点所连的线段平行且相等”,这个基本性质既可作为平移图形之间的性质,又可作为平移作图的依据.
典例1:(2022•大连)如图,在平面直角坐标系中,点A的坐标是(1,2),将线段OA向右平移4个单位长度,得到线段BC,点A的对应点C的坐标是 (5,2) .
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减求解即可.
【解答】解:将线段OA向右平移4个单位长度,得到线段BC,点A的对应点C的坐标是(1+4,2),即(5,2),
故答案为:(5,2).
【点评】本题主要考查坐标与图形变化—平移,解题的关键是掌握点的坐标的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减.
典例2:(2022•毕节市)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(﹣1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(﹣4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,﹣4),…;按此做法进行下去,则点A10的坐标为 (﹣1,11) .
【分析】根据题目规律,依次求出A5、A6……A10的坐标即可.
【解答】解:由图象可知,A5(5,1),
将点A5向左平移6个单位、再向上平移6个单位,可得A6(﹣1,7),
将点A6向左平移7个单位,再向下平移7个单位,可得A7(﹣8,0),
将点A7向右平移8个单位,再向下平移8个单位,可得A8(0,﹣8),
将点A8向右平移9个单位,再向上平移9个单位,可得A9(9,1),
将点A9向左平移10个单位,再向上平移10个单位,可得A10(﹣1,11),
故答案为:(﹣1,11).
【点评】本题主要考查了坐标与图形变化﹣平移,规律型问题,解题的关键是学会探究规律,属于中考常考题型.
考点二、轴对称变换
1.轴对称与轴对称图形
轴对称:把一个图形沿着某一条直线折叠,如果能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也叫做这两个图形成轴对称,这条直线叫做对称轴,折叠后重合的对应点,叫做对称点.
轴对称图形:把一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
2.轴对称变换的性质
①关于直线对称的两个图形是全等图形.
②如果两个图形关于某直线对称,对称轴是对应点连线的垂直平分线.
③两个图形关于某直线对称,如果它们对应线段或延长线相交,那么交点在对称轴上.
④如果两个图形的对应点连线被同一直线垂直平分,那么这两个图形关于这条直线对称.
3.轴对称作图步骤
①找出已知图形的关键点,过关键点作对称轴的垂线,并延长至2倍,得到各点的对称点.
②按原图形的连结方式顺次连结对称点即得所作图形.
4.翻折变换:图形翻折问题是近年来中考的一个热点,其实质是轴对称问题,折叠重合部分必全等,折痕所在直线就是这两个全等形的对称轴,互相重合的两点(对称点)连线必被折痕垂直平分.
【要点诠释】翻折的规律是,折叠部分的图形,折叠前后,关于折痕成轴对称,两图形全等,折叠图形中有相似三角形,常用勾股定理.
典例3:(2022•资阳)如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点.若AB=4,则AE+OE的最小值是( )
A. B. C. D.
【分析】本题为典型的将军饮马模型问题,需要通过轴对称,作点A关于直线BC的对称点A',再连接A'O,运用两点之间线段最短得到A'O为所求最小值,再运用勾股定理求线段A'O的长度即可.
【解答】解:如图所示,作点A关于直线BC的对称点A',连接A'O,其与BC的交点即为点E,再作OF⊥AB交AB于点F,
∵A与A'关于BC对称,
∴AE=A'E,AE+OE=A'E+OE,当且仅当A',O,E在同一条线上的时候和最小,如图所示,此时AE+OE=A'E+OE=A'O,
∵正方形ABCD,点O为对角线的交点,
∴,
∵A与A'关于BC对称,
∴AB=BA'=4,
∴FA'=FB+BA'=2+4=6,
在Rt△OFA'中,,
故选:D.
【点评】本题为典型的将军饮马模型,熟练掌握轴对称的性质,并运用勾股定理求线段长度是解题关键.
典例4:(2022•黔西南州)在如图所示的Rt△ABC纸片中,∠ACB=90°,D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若AE∥DC,∠B=α,则∠EAC等于( )
A.α B.90°﹣α C.α D.90°﹣2α
【分析】由直角三角形斜边上的中线性质和折叠的性质得出CD=BD=AD=ED,∠B=∠DCB=∠DCE=∠CED=α,求出∠EAD=∠AED=180°﹣2α,∠CAD=90°﹣α,即可得出答案.
【解答】解:∵∠ACB=90°,D是斜边AB的中点,
∴CD=BD=AD,
由折叠的性质得:BD=ED,∠B=∠CED,
∴CD=BD=AD=ED,
∴∠B=∠DCB=∠DCE=∠CED=α,
∴∠EDC=180°﹣∠DCE﹣∠CED=180°﹣α﹣α=180°﹣2α,
∵AE∥DC,
∴∠AED=∠EDC=180°﹣2α,
∵ED=AD,
∴∠EAD=∠AED=180°﹣2α,
∵∠B=α,∠ACB=90°,
∴∠CAD=90°﹣α,
∴∠EAC=∠EAD﹣∠CAD=180°﹣2α﹣(90°﹣α)=90°﹣α,
故选:B.
【点评】本题考查了折叠的性质、直角三角形的性质、等腰三角形的判定与性质、平行线的性质、三角形内角和定理等知识,熟练掌握折叠的性质和等腰三角形的性质是解题的关键.
考点三、旋转变换
1.旋转概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的角叫做旋转角.
2.旋转变换的性质
图形通过旋转,图形中每一点都绕着旋转中心沿相同的方向旋转了同样大小的角度,任意一对对应点与旋转中心的连线都是旋转角,对应点到旋转中心的距离相等,对应线段相等,对应角相等,旋转过程中,图形的形状、大小都没有发生变化.
3.旋转作图步骤
①分析题目要求,找出旋转中心,确定旋转角.
②分析所作图形,找出构成图形的关键点.
③沿一定的方向,按一定的角度、旋转各顶点和旋转中心所连线段,从而作出图形中各关键点的对应点.
④ 按原图形连结方式顺次连结各对应点.
【要点诠释】
1.图形变换与图案设计的基本步骤
①确定图案的设计主题及要求;
②分析设计图案所给定的基本图案;
③利用平移、旋转、轴对称对基本图案进行变换,实现由基本图案到各部分图案的有机组合;
④对图案进行修饰,完成图案.
2.平移、旋转和轴对称之间的联系
一个图形沿两条平行直线翻折(轴对称)两次相当于一次平移,沿不平行的两条直线翻折两次相当于一次旋转,其旋转角等于两直线交角的2倍.
典例5:(2022•枣庄)如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
A.(4,0) B.(2,﹣2) C.(4,﹣1) D.(2,﹣3)
【分析】作出旋转后的图形即可得出结论.
【解答】解:作出旋转后的图形如下:
∴B'点的坐标为(4,﹣1),
故选:C.
【点评】本题主要考查图形的平移和旋转,熟练掌握图形的平移和旋转是解题的关键.
典例6:(2022•鞍山)如图,在△ABC中,AB=AC,∠BAC=120°,点D在直线AC上,连接BD,将DB绕点D逆时针旋转120°,得到线段DE,连接BE,CE.
(1)求证:BC=AB;
(2)当点D在线段AC上(点D不与点A,C重合)时,求的值;
(3)过点A作AN∥DE交BD于点N,若AD=2CD,请直接写出的值.
【分析】(1)作AH⊥BC于H,可得BH=AB,BC=2BH,进而得出结论;
(2)证明△ABD∽△CBE,进而得出结果;
(3)当点D在线段AC上时,作BF⊥AC,交CA的延长线于F,作AG⊥BD于G,设AB=AC=3a,则AD=2a,解直角三角形BDF,求得BD的长,根据△DAG∽△DBF求得AQ,进而求得AN,进一步得出结果;当点D在AC的延长线上时,设AB=AC=2a,则AD=4a,同样方法求得结果.
【解答】(1)证明:如图1,
作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH==60°,BC=2BH,
∴sin60°=,
∴BH=,
∴BC=2BH=;
(2)解:∵AB=AC,
∴∠ABC=∠ACB==30°,
由(1)得,
,
同理可得,
∠DBE=30°,,
∴∠ABC=∠DBE,=,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
∴∠ABD=∠CBE,
∴△ABD∽△CBE,
∴;
(3)解:如图2,
当点D在线段AC上时,
作BF⊥AC,交CA的延长线于F,作AG⊥BD于G,
设AB=AC=3a,则AD=2a,
由(1)得,CE=,
在Rt△ABF中,∠BAF=180°﹣∠BAC=60°,AB=3a,
∴AF=3a•cos60°=,BF=3a.sin60°=,
在Rt△BDF中,DF=AD+AF=2a+a=,
BD===a,
∵∠AGD=∠F=90°,∠ADG=∠BDF,
∴△DAG∽△DBF,
∴,
∴=,
∴AG=,
∵AN∥DE,
∴∠AND=∠BDE=120°,
∴∠ANG=60°,
∴AN==a=a,
∴=,
如图3,
当点D在AC的延长线上时,
设AB=AC=2a,则AD=4a,
由(1)得,
CE==4,
作BR⊥CA,交CA的延长线于R,作AQ⊥BD于Q,
同理可得,
AR=a,BR=,
∴BD==2a,
∴,
∴AQ=,
∴AN==a,
∴==,
综上所述:或.
【点评】本题考查了等腰三角形的性质,相似三角形的判定和性质,解直角三角形等知识,解决问题的关键是正确分类和较强的计算能力.








