数学四年级下册密铺教案配套课件ppt

这是一份数学四年级下册密铺教案配套课件ppt，共16页。PPT课件主要包含了活动任务，设计方案，动手实验，交流反思，密铺与图形的角有关等内容，欢迎下载使用。

经历探索哪些图形可以密铺，哪些图形不能密铺的过程，进一步认识密铺的特点，培养空间观念。（重点）根据给定的图形进行设计密铺的图案，感受数学在生活中的应用，会用数学的眼光欣赏美和创造美。（难点）
三角形能不能密铺？四边形可不可以？
解决这个问题需要哪些主要步骤？
你想采取怎样的方式解决问题？（独立完成/小组合）如果是小组合作，怎样进行分工？
把主要步骤、分工写下来。
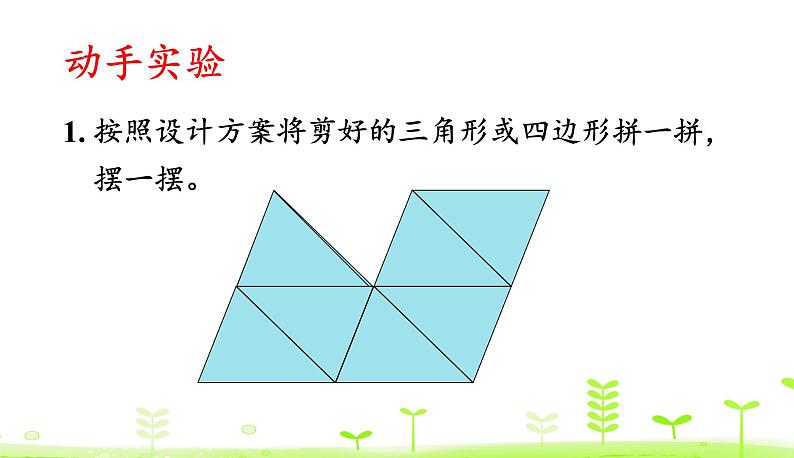
按照设计方案将剪好的三角形或四边形拼一拼，摆一摆。
全班交流密铺的作品，三角形能不能密铺？四边形呢？
观察发现：图形之间都没有空隙，也不重叠，根据密铺的意义可知，三角形和四边形都可以密铺。
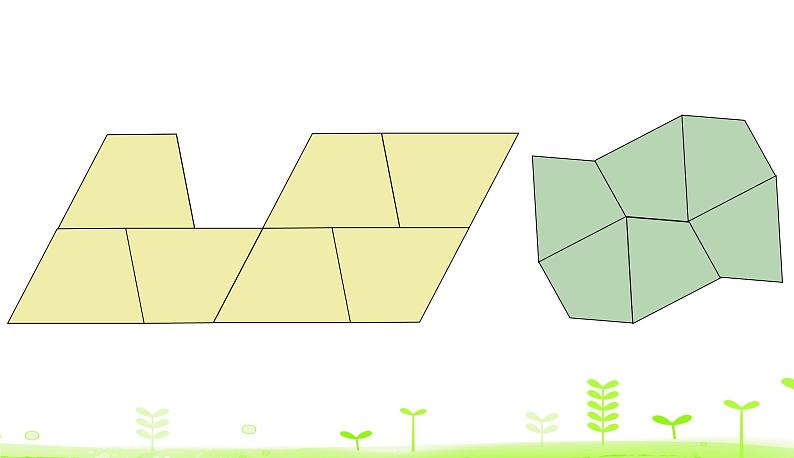
请按照下面的方法试一试，你有什么发现？
我发现：密铺的图形公共顶点处的角的度数合起来正好是 360º。例如：左图：∠1＋∠2＋∠3＋∠1＋∠2＋∠3＝360º；中图：∠1＋∠2＋∠3＋∠4＝360º；右图：∠1＋∠2＋∠3＋∠4＝360º。
在上面的活动中，你有什么收获？还有哪些想要进一步研究的问题？
不是所有的平面图形都可以密铺。看一看，试一试。
正五边形的内角和：＝（5－2）×180°＝540°每个角的度数是：540°÷5=108°，108°×3=324°324°＜360°所以正五边形不能密铺。
由正六边形的内角和＝（6－2）×180°＝720°每个角的度数是：720°÷6＝120° 120°×3＝360°所以正六边形能密铺。
第四幅图是由不规则图形密铺成的图案。
第一幅图是由四边形密铺成的图案
第二幅图是由正六边形密铺成的图案
第三幅图是由不规则图形密铺成的图案
看一看下面的密铺图案，想一想它们是如何形成的。
这节课你们都学会了哪些知识？
1 周有 360 度，如果能正好把这 360 度铺严（即在公共顶点上几个角度数的和正好是 360度），那么就可以密铺。