2023届宁夏六盘山高级中学高三（提升班）上学期第一次月考数学（文）试题（解析版）

2023届宁夏六盘山高级中学高三（提升班）上学期第一次月考数学（文）试题

一、单选题

1．如图，阴影部分用集合、、表示为

A． B． C． D．

【答案】C

【详解】如图，观察图形可知，阴影是B的补集与集合A的交集，即，故选C.

2．函数的零点所在的大致区间是（    ）

A． B．

C． D．

【答案】C

【分析】首先判断函数的单调性，再根据零点存在性定理判断即可.

【详解】解：的定义域为，又与在上单调递增，

所以在上单调递增，

又，，，

所以，所以在上存在唯一的零点.

故选：C

3．已知，则a，b，c的大小关系为（    ）

A． B．

C． D．

【答案】C

【分析】根据对数的运算性质和对数函数的单调性，分别求得的取值范围，即可求解.

【详解】由，

可得，

又由，所以，

又因为，所以.

所以．

故选：C.

4．在中，已知，则是（    ）

A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等腰三角形或直角三角形

【答案】D

【分析】结合降幂公式得到，所以或，从而可判断三角形的形状.

【详解】因为，所以，即，所以或，故或，所以是等腰三角形或直角三角形，

故选：D.

5．已知角的顶点为坐标原点，始边与轴的非负半轴重合，终边经过点，则（    ）

A． B． C． D．

【答案】B

【分析】根据角终边上点的坐标，求得，代入二倍角公式即可求得的值．

【详解】因为终边上点，所以，

所以

故选：B．

6．函数在单调递增，在单调递减，则的值为（    ）

A． B．1 C．2 D．

【答案】A

【分析】由题意可得，求得，结合函数的单调区间确定，即可确定的值.

【详解】依题意得：，

，

又在单调递减，，

解得：，，

故选：

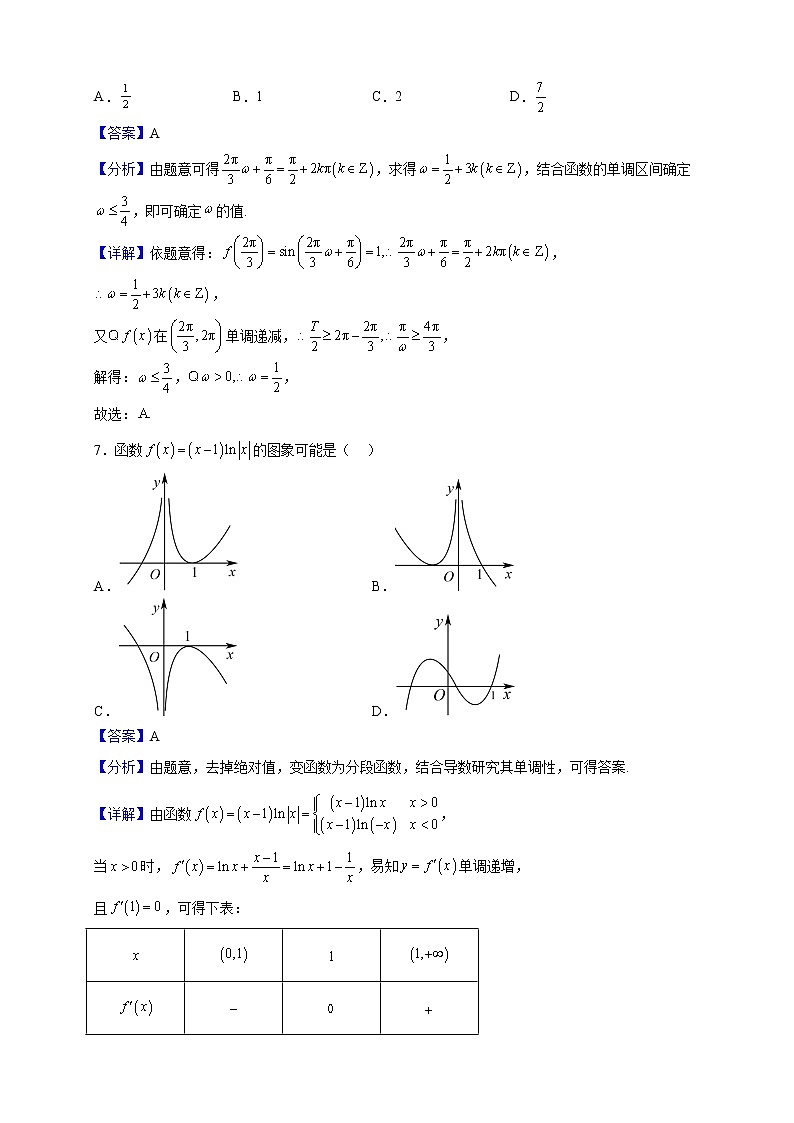
7．函数的图象可能是（    ）

A． B．

C． D．

【答案】A

【分析】由题意，去掉绝对值，变函数为分段函数，结合导数研究其单调性，可得答案.

【详解】由函数，

当时，，易知单调递增，

且，可得下表：

则，

当时，，令，

，令，解得，可得下表：

则，即，则单调递增.

故选：A.

8．已知，分别是方程，的根，则（    ）

A．1 B．2 C． D．

【答案】B

【分析】由题意可得，分别是函数，的图象与直线交点的横坐标，由于的图象与图象关于直线对称，而直线也关于直线对称，所以两交点的中点就是直线与的交点，求出交点坐标，再利用中点坐标公式可求出的值

【详解】由题意可得是函数的图象与直线交点的横坐标，是函数图象与直线交点的横坐标，

因为的图象与图象关于直线对称，而直线也关于直线对称，

所以线段的中点就是直线与的交点，

由，得，即线段的中点为，

所以，得，

故选：B

9．若实数，满足，，则“”是“”的（    ）

A．充分不必要条件 B．必要不充分条件

C．充分必要条件 D．既不充分也不必要条件

【答案】C

【详解】构造函数 ，故函数在上单调递增，即由“” 可得到“”,反之，由“”亦可得到“”

选C

10．已知函数的最小正周期为，其最小值为，且满足，则（    ）

A． B． C． D．

【答案】C

【分析】化简解析式，根据的最小正周期、最小值以及对称中心，依次求得的值.

【详解】

，

其中.

依题意；.

所以，不妨设.

所以，

由，令，得，

所以，

，由于，所以.

故选：C

11．某种商品在今年1月份价格降低10%，在此之后由于市场供求关系的影响，价格连续三次上涨，使目前售价与1月降价前的价格相同.则这三次上涨的平均回升率是（    ）

A． B． C． D．

【答案】D

【分析】设该商品在今年1月份的价格为a(a>0),这次价格的平均回升率为x，结合题意构造等量关系，求解.

【详解】根据题意，设该商品在今年1月份的价格为a(a>0),这次价格的平均回升率为x,则有

解得：

故选：D

【点睛】本题考查的是函数的实际应用问题，考查了学生实际应用，数学运算的能力，属于中档题.

12．已知函数的定义域为R，且对任意，恒成立，则解集为（    ）

A． B． C． D．

【答案】B

【分析】由题干条件构造函数，得到的单调性，从而对变形，利用函数单调性解不等式.

【详解】由得，

记，则在R上单调递增.

由得，

即，

∴，

∴.

故选：B.

二、填空题

13．计算：____________

【答案】

【分析】切化弦，通分后结合二倍角和两角和差正弦公式可化简求得结果.

【详解】.

故答案为：.

14．已知命题，.若为假命题，则的取值范围为___________

【答案】

【分析】首先写出命题的否命题，根据为假命题即可得出为真命题即可求出的取值范围.

【详解】为假命题

为真命题，故

在 的最小值为

∴

故答案为：

15．函数，的部分图象如图所示，则______．

【答案】0

【分析】由题可得，函数的周期T＝8，求出，得出，即得.

【详解】由图象可知，函数的周期T＝8，

所以，故，

因为，，

所以．

故答案为：0.

16．函数，，若，则________．

【答案】-1

【分析】根据解析式先求出，再代入求出.

【详解】因为， ，所以.

当时，，解得：；

当时，，无解.

所以.

所以

故答案为：-1

三、解答题

17．设为实数，函数.

(1)求的极值；

(2)若曲线与轴仅有一个交点，求的取值范围.

【答案】(1)极小值为，极大值为

(2)

【分析】（1）函数连续可导，只需讨论满足的点附近的导数的符号的变化情况来确定极值点，求出极值（2）曲线与轴仅有个交点,等价于函数的图象与直线仅有个交点，数形结合即可求解

【详解】（1），

令，解得，

当时，；当时，；当时；，

所以，当时，取得极大值；

当时，取得极小值.

（2）由,得

由题意知,曲线与轴仅有个交点,等价于函数的图象与直线仅有个交点，

因为,

当或时,当时,,

所以函数在区间和上单调递增,

在区间上单调递减,

所以函数的极大值为,函数的极小值为,

如图所示：

由图可知，和的图象仅有一个公共点,当且仅当:或,

即或,

所以,实数的取值范围为

18．已知函数(a>0且a≠1).

（1）若a>1，求函数f(x)的单调区间；

（2）若函数f(x)的最小值为，求a的值.

【答案】（1）在上单调递增，在上单调递减，（2）

【分析】（1）首先求出函数的定义域，再根据复合函数的单调性判断可得；

（2）令，则，根据对数函数的性质分类讨论计算可得；

【详解】解：（1）因为，所以，解得，即函数的定义域为，

，

因为在上单调递增，在上单调递减，又，所以在定义域上单调递增，所以函数在上单调递增，在上单调递减，

（2）由（1）令，则，，当时，函数在上单调递增，函数不存在最小值，故舍去；

当时，函数在上单调递减，，所以，解得；

19．已知函数

(1)求的对称轴方程；

(2)求在区间上的单调区间

【答案】(1)

(2)在单调减，在单调增

【分析】（1）由三角恒等变换将化简为的形式，再由对称轴公式计算即可.

（2）由（1）中的解析式令，求得单调增区间，再得到减区间即可.

【详解】（1）

令解得

所以对称轴发方程为

（2）由（1）知

令，

解得，

当时，单调增区间为

又因为区间为，

所以增区间为，减区间为

20．△ABC中，内角A，B，C的对边分别为a，b，c，且△ABC的外接圆半径R满足.

(1)求角C；

(2)若，求△ABC周长的取值范围.

【答案】(1)

(2)

【分析】（1）利用正弦定理进行边角转化，再结合三角恒等变换化简整理求解；（2）利用正弦定理进行边化角，再结合三角恒等变换化简整理可得，再以为整体结合三角函数求范围.

【详解】（1）由正弦定理，可得，

∴，

所以，则，

因为，所以.

（2）∵，，由正弦定理得，

∴，，

∴△ABC的周长：，

由，得，∴，

∴a＋b＋c的取值范围，即△ABC周长的取值范围是.

21．已知.

(1)当时，求曲线在点处的切线方程；

(2)若对恒成立，求的取值范围.

【答案】(1)

(2)

【分析】（1）利用导数的几何意义以及直线方程的点斜式即可求解.

（2）分离参数，转化成不等式恒成立问题，利用导数求最值即可.

【详解】（1）当时，，，

，，

所以切线方程为：，即.

（2）恒成立，即在上恒成立，

设，，

令，得，

在上，，

所以函数在上单调递减，

所以，，

故有.

22．在平面直角坐标系中，直线的参数方程为（为参数，．以坐标原点为极点，轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为．

(1)求曲线的直角坐标方程；

(2)若直线与曲线交于两点，当时，求直线的普通方程．

【答案】(1)

(2)或

【分析】（1）根据极坐标与直角坐标的互化公式求解即可；

（2）根据题意，结合直线参数方程的几何意义及弦长公式求解得直线的倾斜角，再求普通方程即可.

【详解】（1）解：由得，

因为，

所以，即.

（2）解：将（为参数，代入，

整理得．

设所对应的参数分别为，，

则，．

所以，

解得，所以或，

故直线的参数方程为（为参数）或（为参数），

所以直线的直角坐标方程为或

23．已知函数.

(1)求函数的最小值；

(2)若正实数满足，且对任意的正实数恒成立，求的取值范围.

【答案】(1)

(2)

【分析】（1）化简函数，由分段函数的性质可得最小值；

（2）利用基本不等式得出的最小值，代入不等式求解可得的取值范围.

【详解】（1），可知当时，函数的最小值；

（2）由（1）得，，当且仅当时取等号，即的最小值为，对任意的正实数恒成立，，即，解得，故的取值范围是．