2023届安徽省六安第二中学高三上学期第四次月考数学试题（解析版）

2023届安徽省六安第二中学高三上学期第四次月考数学试题

一、单选题

1．设集合，，则（    ）

A． B． C． D．

【答案】D

【分析】利用交集运算即可.

【详解】因为，，所以

故选：D

2．设复数满足，则（    ）

A． B． C． D．

【答案】C

【分析】根据复数的运算，化简复数可得，即可得到结果.

【详解】因为，

所以.

故选：C.

3．若直线的倾斜角为，则的值为（    ）

A．2 B． C． D．4

【答案】A

【分析】首先得到直线的斜率，从而得到，

再利用正弦余弦的二倍角公式将弦化切，最后代入计算可得.

【详解】因为直线的斜率，

设倾斜角为，所以，

由

，

故选：A.

4．若成等差数列；成等比数列，则等于（    ）

A． B． C． D．

【答案】B

【分析】根据等差数列和等比数列的性质列出方程，求出，，求出.

【详解】由题意得：，

设的公比为，则，，

解得：，

.

故选：B

5．2022年卡塔尔世界杯是第22届世界杯足球赛，比赛于2022年11月21日至12月18日在卡塔尔境内7座城市中的12座球场举行．已知某足球的表面上有四个点A、B、C、P满足PA＝BC＝5，，，则该足球的表面积为（    ）

A． B． C． D．

【答案】D

【分析】把四面体外接球问题扩展到长方体中，求出长方体外接球半径为R，进而求出结果．

【详解】因为PA＝BC，，，所以可以把A，B，C，P四点放到长方体的四个顶点上，将四面体放入长方体中，四面体各边可看作长方体各面的对角线，如图所示：

则该足球的表面积为四面体A-BCP外接球的表面积，即为长方体外接球的表面积，

设长方体棱长为a，b，c，则有，，，

设长方体外接球半径为R，则有，解得，

所以外接球的表面积为：.

故选：D．

6．化简的结果是（    ）

A．1 B． C．2 D．

【答案】A

【分析】先利用“切化弦”思想，进行通分运算，根据辅助角公式结合二倍角公式化简即可得结果.

【详解】

.

故选：A.

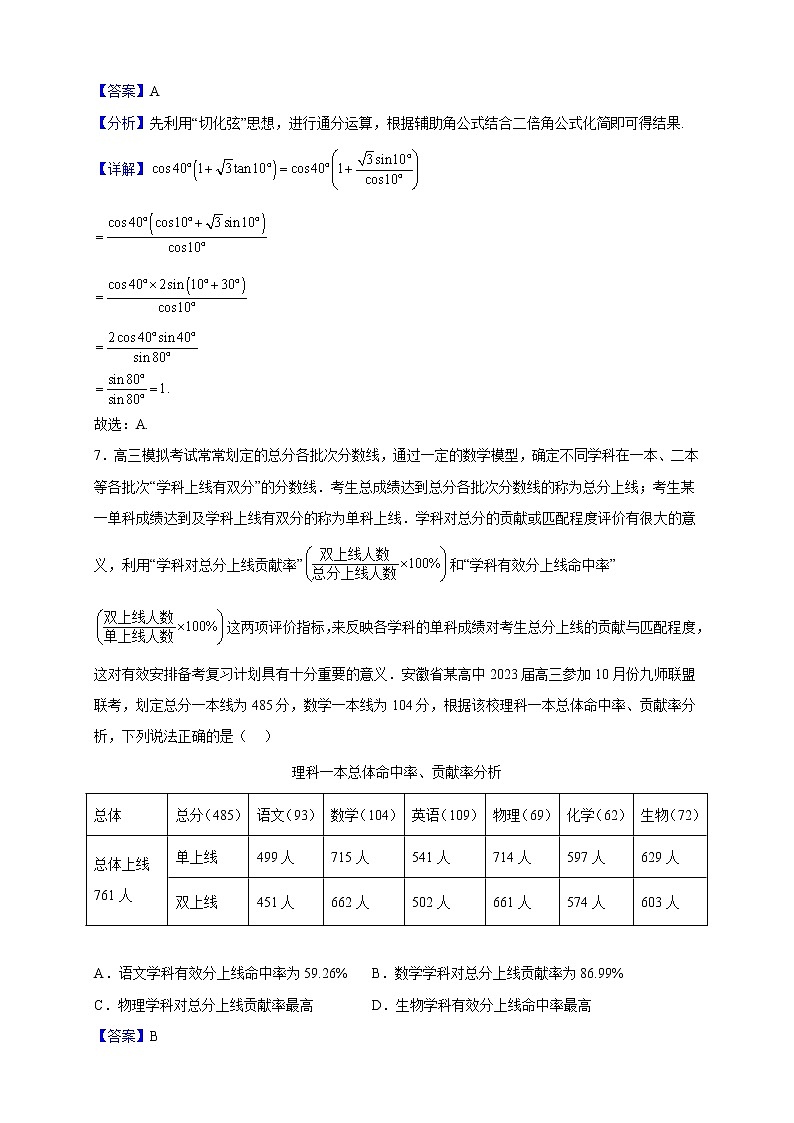
7．高三模拟考试常常划定的总分各批次分数线，通过一定的数学模型，确定不同学科在一本、二本等各批次“学科上线有双分”的分数线．考生总成绩达到总分各批次分数线的称为总分上线；考生某一单科成绩达到及学科上线有双分的称为单科上线．学科对总分的贡献或匹配程度评价有很大的意义，利用“学科对总分上线贡献率”和“学科有效分上线命中率”这两项评价指标，来反映各学科的单科成绩对考生总分上线的贡献与匹配程度，这对有效安排备考复习计划具有十分重要的意义．安徽省某高中2023届高三参加10月份九师联盟联考，划定总分一本线为485分，数学一本线为104分，根据该校理科一本总体命中率、贡献率分析，下列说法正确的是（    ）

A．语文学科有效分上线命中率为59.26% B．数学学科对总分上线贡献率为86.99%

C．物理学科对总分上线贡献率最高 D．生物学科有效分上线命中率最高

【答案】B

【分析】根据“学科有效分上线命中率”和“学科对总分上线贡献率”的公式计算、比较可得答案.

【详解】根据题意可得：语文学科有效分上线命中率为，故A不正确；

生物学科有效分上线命中率为，

化学学科有效分上线命中率为，故D不正确；

数学学科对总分上线贡献率为，故B正确；

物理学科对总分上线贡献率，故C不正确.

故选：B

8．定义在上的奇函数满足时，都有不等式成立，若，，，则a，b，c的大小关系是（    ）

A． B． C． D．

【答案】A

【分析】根据构造函数，可得函数为减函数，又由为奇函数可知为偶函数，据此可比较大小.

【详解】当时不等式成立，

，

在上是减函数．

则，，，

又函数是定义在上的奇函数，

是定义在上的偶函数，则，

，在上是减函数，

，则，

故选：A．

二、多选题

9．下列说法正确的是（    ）

A．若函数的定义域为，则函数的定义域为

B．图象关于点成中心对称

C．的最大值为

D．幂函数在上为减函数，则的值为1

【答案】BD

【分析】根据函数的定义域、对称性、最值、单调性等知识对选项进行分析，从而确定正确答案.

【详解】A选项，函数的定义域为，

所以对于函数，有，即的定义域是，A选项错误.

B选项，，所以图象关于点成中心对称，B选项正确.

C选项，，所以，

即的最小值为，C选项错误.

D选项，是幂函数，

所以，解得或，

当时，，在上递减，

当时，，在上递增，

所以D选项正确.

故选：BD

10．已知函数的部分图像如图所示，将的图像向左平移个单位长度，再向上平移1个单位长度后得到函数的图像，则（    ）

A． B．

C．的图像关于点对称 D．在上单调递减

【答案】AD

【分析】利用函数图像先把解析式求出来，然后逐项分析即可.

【详解】由图像可知函数的最大值为2，最小值为，

所以，，

又，又，

所以

又，所以，所以，故正确，

将的图像向左平移个单位长度，

再向上平移1个单位长度后得，故错误．

由，所以的图像关于点对称，故错误．

由即，所以选项正确 .

故选：．

11．瑞士著名数学家莱昂哈德·欧拉在年提出：三角形的外心、重心、垂心位于同一直线上，这条直线被后人称为三角形的“欧拉线”．在平面直角坐标系中作，，点，点，且其“欧拉线”与圆相切，则下列结论正确的是（    ）

A．的“欧拉线”方程为

B．圆上点到直线的最大距离为

C．若点在圆上，则的最小值是

D．圆与圆有公共点，则的取值范围是

【答案】ACD

【分析】根据等腰三角形三线合一的性质确定“欧拉线”为的垂直平分线即可判断A，利用圆的性质求出圆心到直线的距离即可判断B，由题意转化为求出圆心到原点的距离即可判断C，根据两圆的位置关系，列出圆心距与半径和、差的不等关系即可判断D.

【详解】对于A选项，因为，则的外心、重心、垂心都在线段的垂直平分线上，，线段的中点为，所以，的“欧拉线”方程为，即，A对；

对于B选项，圆心，则，圆心到直线的距离为，

所以，圆上点到直线的最大距离为，B错；

对于C选项，记点，因为，则原点在圆外，

所以，的最小值为，C对；

对于D选项，圆的圆心为，半径为，由题意可得，即，解得，D对．

故选：ACD

12．棱长为1的正方体中，为底面的中心，是棱上一点，且，，为线段的中点，下列命题中正确的是（  ）

A．三棱锥的体积与的取值无关

B．当时，点Q到直线AC的距离是

C．当时，

D．当时，过三点的平面截正方体所得截面的周长为

【答案】ABD

【分析】根据锥体体积计算、点线距离、线线垂直、正方体的截面等知识对选项进行分析，从而确定正确答案.

【详解】对选项A：由，因为到平面的距离为定值，

且的面积为定值，所以三棱锥的体积跟的取值无关，所以A正确；

对选项B：当时，是的中点，

，

，所以为锐角，

所以,

所以点Q到直线AC的距离是，所以B正确.

对选项C：当时，，可得，，

取的中点分别为，连接，则，

在直角三角形中，，

则，所以不成立，所以C不正确．

对选项D：当时，取，连接，则，又，

所以，所以共面，即过三点的正方体的截面为，

由，则是等腰梯形，且，

所以平面截正方体所得截面的周长为，所以D正确；

故选：ABD

三、填空题

13．命题“”的否定是____________．

【答案】，

【分析】根据命题的否定的定义，直接写出答案.

【详解】命题“”的否定是“，”

故答案为：，

14．设为的外接圆圆心，若，则在上投影向量的模为_________

【答案】##

【分析】根据向量的线性运算及三角形外接圆的性质，利用勾股定理及锐角三角函数，结合向量的投影向量及向量的模公式即可求解.

【详解】由得,

所以为的中点，

又因为为的外接圆圆心，

所以,,

所以,

在中，,

,

所以在上的投影为,

所以在上投影向量为,    

所以在上投影向量的模为.

故答案为：.

15．在中，角A，B，C所对的边分别为a，b，c，且，，成等差数列，若，则的面积最大值为______．

【答案】

【分析】利用正弦定理化简已知条件，由此求得，利用余弦定理和基本不等式求得的最大值，进而求得三角形面积的最大值.

【详解】由题意得，，

由正弦定理得，

又，所以，则，，

因为，所以，

当且仅当时等号成立，

所以．

故答案为：

16．若是函数的极值点，数列满足，设，记表示不超过的最大整数．设，若不等式对恒成立，则实数的最大值为__________．

【答案】2023

【分析】由题可算得，求得，，根据，计算得的最小值为2023即可解决.

【详解】由题知，，

所以，

因为是函数的极值点，

所以，即有，

是以2为首项，3为公比的等比数列，

，则累加得，

所以，

，则，

所以

，

所以的最小值为2023，

若不等式对恒成立，则只需即可，

所以，所以实数的最大值为2023．

故答案为：2023

四、解答题

17．已知圆过点，，．

(1)求圆的方程；

(2)设直线经过点，且与圆相交于，两点，且，求直线的方程．

【答案】(1)

(2)或

【分析】（1）利用向量，得，进而可求出圆心和半径，得到圆的方程；

（2）由已知，求出圆心到直线的距离，再利用点到直线的距离公式，列出相应方程，即可求出直线的斜率，进而得到直线的方程.

【详解】（1），，，，

且，得，

故为直径，的中点即为圆的圆心，半径为，故圆心为，所以，

圆的方程为

（2）设圆心到直线的距离为，则，解得，

对于直线，当直线的斜率不存在时，为，满足，

当直线的斜率存在时，设为，故，解得，

故此时为；

综上，直线的方程为或

18．已知数列满足：,数列的前n项和

(1)求数列的通项公式;

(2)设,求数列的前n项和．

【答案】(1)

(2)

【分析】(1)根据数列的递推关系式判断数列类型求出通项公式,根据的前n项和,利用,求出数列的通项公式即可,注意检验;

(2)根据数列通项公式的特殊性,利用错位相减法,求出其前n项和即可.

【详解】（1）解:由题知

,

是以2为公比的等比数列,

,

的前n项和,

时,

当时,,

故,

综上:;

（2）由(1)知,

,

,①

,②

②-①可得:

故.

19．已知向量，向量，且函数．

(1)求函数的单调递增区间；

(2)在中，角A，B，C所对的边分别为a，b，c且角A满足．若，BC边上的中线长为3，求的面积．

【答案】(1)；

(2).

【分析】（1）根据数量积的坐标运算可得，解，，可得到函数的单调递增区间；

（2）由已知可解出，根据中线的向量表示以及，即可得到，进而求出的面积．

【详解】（1）因为，

由，可得，，，

所以函数的单调递增区间为.

（2）由，得，

因为，所以，所以，所以.

又，则，则.

又BC上的中线长为3，则，即有.

所以，，即，

所以，

所以，.

20．如图，在三棱锥中，，为的中点，．

(1)证明：平面平面；

(2)若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积．

【答案】(1)证明见解析

(2)

【分析】（1）先证明平面，再由平面与平面垂直的判定定理证明平面平面；

（2）建立空间直角坐标系，计算平面和平面的法向量，根据二面角的大小为，求出的长，计算三棱锥的体积.

【详解】（1）因为，O是中点，所以，

又，，所以平面，

因为平面，平面平面.

（2）以O为坐标原点，为轴，为y轴，过O且垂直的直线为x轴，建立如图空间直角坐标系，为边长为1的等边三角形，

则，，，设，，

因为，所以 ，

所以，，设为平面的一个法向量，

则，即，令，

又平面的一个法向量为，所以，

解得，所以，

，所以，

所以三棱锥的体积为

21．观察实际情景，提出并分析问题

（1）实际情境

百年大计，教育为本．六安二中肇始于1923年创办的“海峰女子学校”，在近百年的追梦历程中，经历着沧桑、续写着辉煌．她是全省首批省级示范高中，也是一所规模宏大、条件先进、质量上乘、特色鲜明的现代化高级中学.2023年时值百年校庆，近百年来，海峰先贤的家国担当意识构成了六安二中厚重人文历史的基石，也是一直以来六安二中人坚守的信念．

（2）提出问题

六安二中校庆组委会宣传办公室需要氦气用于制作气球装饰校园，化学实验社团主动承担了这一任务，社团成员提出如何制备氦气，才能使成本最低？

（3）分析问题

校庆需要氦气用于制作气球装饰校园，社团已有的设备每天最多可制备氦气，按计划社团必须在天内制备完毕．社团成员接到任务后，立即以每天的速度制备氦气．

（4）收集数据

已知每制备氦气所需的原料成本为百元．若氦气日产量不足，日均额外成本为（百元）；若氦气日产量大于等于，日均额外成本为（百元）．制备成本由原料成本和额外成本两部分组成．

（5）建立模型

根据分析问题和收集数据，写出总成本（百元）关于日产量的关系式．

（6）问题解决

化学实验社团每天制备多少升氦气时，总成本最少？并求出最低成本．

（7）问题拓展

数学与我们日常生活密切相关，日常生活中的许多问题来源于数学思想的应用． 在上述模型的建立的过程中，我们在掌握一定的数学基础的前提下选择了不同的函数模型，利用求出对应的函数形式，否定了其它的函数模型，运用数学原理求解出行之有效的最优化方案．

【答案】（5）；（6）当社团每天制备氦气时，总成本最少，最低成本为百元．

【分析】（5）若每天生产氦气，则需生产天，由解出，气日产量不足与产量大于等于，即可得到分段函数；

（6）当时，利用基本不等式即可求出当时，取得最小值，换元，令，即，，即可求出答案.

【详解】(5)建立模型：若每天生产氦气，则需生产天，，则；

若氦气日产量不足，则氦气的平均成本为百元；

若氦气日产量大于等于，则氦气的平均成本为百元；

．

(6)    问题解决：当时，（当且仅当取等号）

当时，取得最小值；

当时，，令，则，，

则当，即时，取得最小值；

综上所述：当社团每天制备氦气时，总成本最少，最低成本为百元．

22．已知函数，函数是定义在的可导函数，其导数为，满足．

(1)若在上单调递减，求实数取值范围；

(2)对任意正数，试比较与的大小．

【答案】(1)

(2)

【分析】（1）根据在上单调性得到不等式，转化为恒成立，结合基本不等式求出，得到，求出实数的取值范围；

（2）构造，求导后得到在上是减函数，令，换元后得到，由得到，变形得到，，结合第一问得到，，从而证明出结论.

【详解】（1）∵在上单调递减，

∴，，

即恒成立，又，

当且仅当，即时等号成立，故，

∴，∴，

又，∴，

∴，

∴的取值范围是；

（2）令，得，

∵，

∴，

又，

∴，

∴在上是减函数．

∵与均大于0，记，

令，则，

由，得，即，

∴，

∴，，

由（1）知当时，在上单调递减，

∴时，，即，

∴，从而有，

即．

【点睛】利用函数与导函数的相关不等式构造函数，然后利用所构造的函数的单调性解不等式，是高考常考题目，以下是构造函数的常见思路：

比如：若，则构造，

若，则构造，

若，则构造，

若，则构造.