专题 18.44 平行四边形存在性问题（专项练习）-八年级数学下册基础知识专项讲练（人教版）

这是一份专题 18.44 平行四边形存在性问题（专项练习）-八年级数学下册基础知识专项讲练（人教版），共50页。
专题 18.44 平行四边形存在性问题（专项练习）
1．如图，AC是平行四边形ABCD的对角线．
(1)尺规作图：作线段AC的垂直平分线l（不写作法，保留作图痕迹）；
(2)直线l分别交AB，AC，CD于点E，F，G．猜想DG与BE存在的数量关系，并证明你猜想的结论．





2．如图1，在平行四边形ABCD中，E为边CD上一动点，连接BE交对角线AC于点F，点M为线段BF上一点，连接AM．
(1)如图1，若对角线AC⊥AB，点M是BF的中点，，，求BC的长；
(2)如图2，若，，AC的垂直平分线交BE的延长线于点G，连接AG，CG，AM平分∠BAC交BE于点M，求证：；
(3)如图3，当点E在运动过程中满足BCE为等边三角形时，若；在BCE内部是否存在一点P使有最小值，若存在，直接写出的最小值，若不存在，请说明理由．





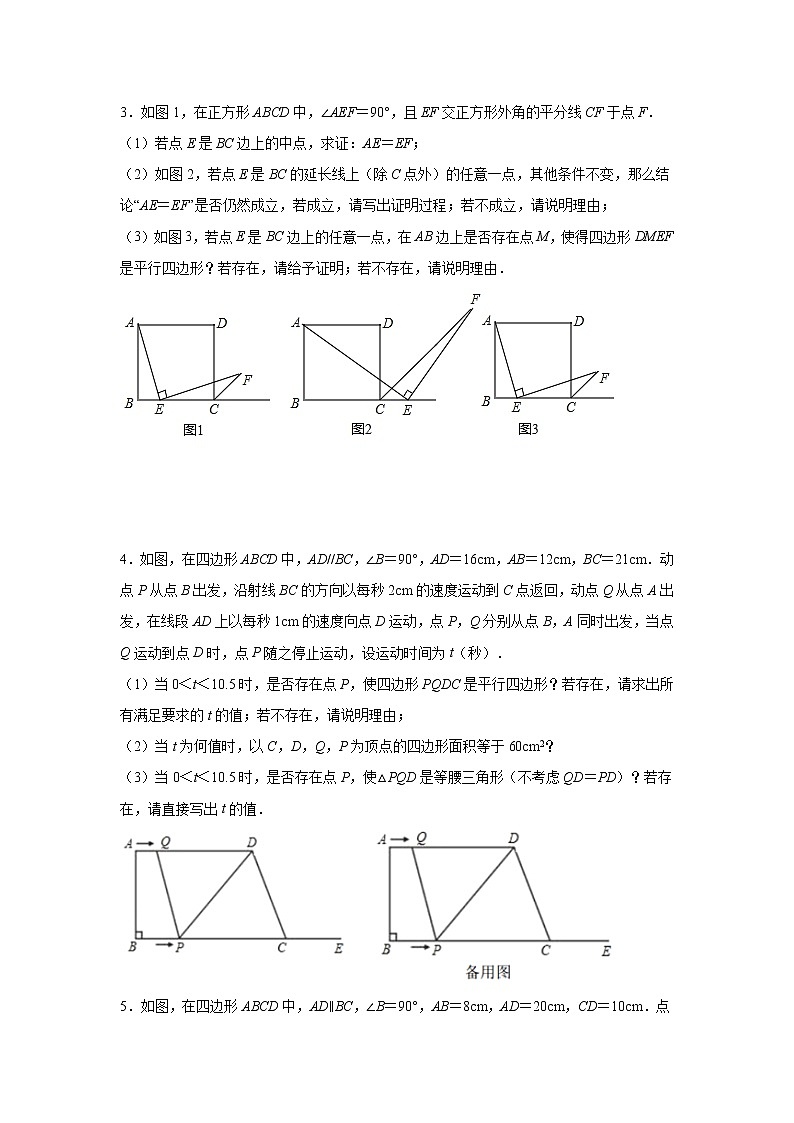
3．如图1，在正方形ABCD中，∠AEF＝90°，且EF交正方形外角的平分线CF于点F．
（1）若点E是BC边上的中点，求证：AE＝EF；
（2）如图2，若点E是BC的延长线上（除C点外）的任意一点，其他条件不变，那么结论“AE＝EF”是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由；
（3）如图3，若点E是BC边上的任意一点，在AB边上是否存在点M，使得四边形DMEF是平行四边形？若存在，请给予证明；若不存在，请说明理由．




4．如图，在四边形ABCD中，AD//BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm．动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动到C点返回，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动时间为t（秒）．
（1）当0＜t＜10.5时，是否存在点P，使四边形PQDC是平行四边形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由；
（2）当t为何值时，以C，D，Q，P为顶点的四边形面积等于60cm2？
（3）当0＜t＜10.5时，是否存在点P，使△PQD是等腰三角形（不考虑QD＝PD）？若存在，请直接写出t的值．

5．如图，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8cm，AD＝20cm，CD＝10cm．点P从点A出发，以2cm/s的速度沿线段AD向点D运动；同时点Q从点C出发，以3cm/s的速度沿BC向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设P、Q运动时间为t秒，回答下列问题：
（1）BC＝_______cm．
（2）求t为何值时四边形PQCD是平行四边形．
（3）求t为何值时四边形PQBA是矩形．
（4）是否存在t的值，使得△DQC是等腰三角形．若存在请直接写出t的值，若不存在，请说明理由．



6．如图，在四边形ABCD中，，，，，．
（1）求AB的长；
（2）动点P从点B出发，沿射线BC以每秒2个单位长度的速度运动，同时动点Q从点A出发，沿线段AD以每秒1个单位长度的速度运动，当点Q运动到点D时，两点同时停止运动，设运动的时间为t秒．
①当t为何值时，以P、Q、D、C为顶点的四边形为平行四边形？
②是否存在点P，使是以PQ为腰的等腰三角形？若存在，请直接写出相应的t的值；若不存在，请说明理由．




7．如图，在四边形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动到C点返回，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t（秒）．
（1）当t为何值时，四边形PQDC是平行四边形；
（2）当t为何值时，以C，D，Q，P为顶点的四边形面积等于60cm2？
（3）当0